44.1 Introduction

This chapter explains how models created by other modelers can be imported into Parasolid.

A model can only be successfully imported if its topology can be expressed as valid Parasolid topology, and its geometry corresponds to valid Parasolid geometric types.

There are two routes for importing external model data. These are:

Trimmed Surface Import route
BREP import route

Which one to use in a given situation is dependent on whether the application knows the BREP topology of the model. When this is known use the BREP route. When the topology isn't known the data must be supplied in the form of trimmed surfaces (that is, as surfaces bounded by loops of surface parameter (SP) curves) in order to make use of the Trimmed Surface route.

[back to top]

44.2 Trimmed surface import route - summary

[back to top]

44.3 Requirements for data import using the trimmed surface import route

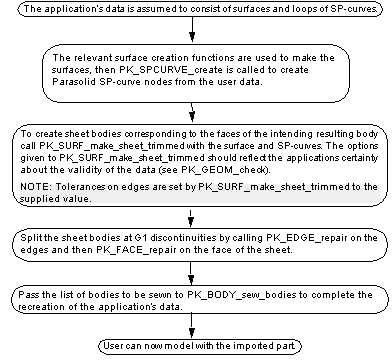
To model successfully in Parasolid with externally created models, there are some requirements that the imported data must satisfy. This section explains these requirements.

[back to top]

44.3.1 SP-curve data

Introduction

To create an SP-curve from surface and uv-space B-spline data call PK_SPCURVE_create. The surface given to PK_SPCURVE_create can be any Parasolid surface provided that it is an orphan. It is permissible for this surface to contain parametric singularities.

You can simplify geometry using PK_BODY_simplify_geom or PK_FACE_simplify_geom. See Section 40.1, "Simplifying geometry", for more information.

Criteria

SP-curves are NURBs in a surface parameter space. They can be of any degree and may be rational, and are supported on all Parasolid surface types.

Note: All SP-curves generated by Parasolid for its own use, e.g. during a PK_EDGE_set_precision operation, are non-rational quadratic curves.

SP-curves are allowed to cross seams on periodic surfaces. There is no need for the application to artificially split curves here.
SP-curves may end at parametric singularities of the underlying (basis) surface, but may not pass through them. For example, a line of longitude on a sphere cannot be represented by a single SP-curve. Parasolid allows the creation of SP-curves which represent degenerate surface boundaries, though PK_SURF_make_sheet_trimmed does not allow them to be incorporated into subsequent sheet bodies.
SP-curves must be G1 in their basis surface parameter space, as well as being G1 in 3-space.

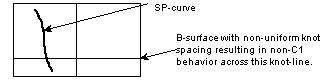
Figure 44-1 SP-curve in 3-space

The SP-curve in Figure 44-1 is G1 in 3-space. However, since its underlying NURB surface is not C1, the uv-space representation of the same curve has a kink in it, i.e. the SP-curve is non-G1 in u, v space. Therefore it is necessary for the curve to be split into two SP-curves. When required, PK_SPCURVE_create optionally handles this splitting though it can only be done for surfaces for which Parasolid can detect discontinuities, e.g. it is not possible for Foreign Geometry basis surfaces.

Figure 44-2 SP-curve is G1 in 3-space, but not in uv-space

Note: Another consequence of the G1 parameter space requirement is that multi-segment linear curves are not allowed. Therefore, all applications making use of piecewise linear curves must convert them to G1 quadratics or higher order.

SP-curves and their control vertices are allowed to cross the boundary of a bounded surface such as a B-surface, though this deviation must be within the continuation region of the surface.
SP-curves are allowed to be closed, and may have a periodic parametrization if the curve is G1 in both 3-space and surface parameter space at its ends. Curves not satisfying the G1 condition are viewed as non-periodic, and are not attachable to pure ring edges.
Some SP-curves cause problems due to extremely small radii of curvature:

Figure 44-3 shows a perfectly well-behaved curve except for a small hook region at one end. Such high curvature can sometimes result from the underlying surface having extremely non-uniform knot spacing.

Figure 44-3 SP-curve with small hook

Figure 44-4 shows an SP-curve with a high curvature S-bend in the middle of the curve. As it isn't guaranteed that PK_SPCURVE_create flags all such configurations, it is inevitable that some examples like these find their way into models, resulting in a corresponding degradation in reliability.

Figure 44-4 SP-curve with high curvature S-bend in the middle

It is extremely difficult to specify exact figures for the minimum radius of curvature which imported SP-curves should meet in order that Parasolid models with the part reliably. Therefore these previous examples are guidelines as to which configurations are likely to be problematic.

[back to top]

44.3.2 DOC0276Trimmed surface data passed into PK_SURF_make_sheet_trimmed

Introduction

To create a sheet body, with a single face, from given surface geometry for the face and curve geometry for the edges, use PK_SURF_make_sheet_trimmed. Using this method of creation the topology of the resulting sheet is inferred from the geometry.

Faces in Parasolid obey a rule for determining on which side of a boundary the face lies. Namely:

"With the face normal upward and the tangent direction of the boundary curve forward, the area of surface within the face is on the left."

If the data supplied to PK_SURF_make_sheet_trimmed implies the area of the surface within the face is on the right then the face sense is automatically set such that the outward side of the face is the reverse side of the surface. This then restores the 'on the left' rule.

The front side of the sheet can, in any case, easily be switched using PK_BODY_reverse_orientation.

As PK_SURF_make_sheet_trimmed is designed for importing geometric data from other solid modelers which work to coarser accuracies than Parasolid, the geometry that is supplied need not conform to Parasolid's strict tolerances.

Criteria

It is important that the SP-curves in each individual loop supplied are ordered in the correct sequence around that loop, with the intended face on the left when viewed in a direction opposing the intended face normal. PK_SURF_make_sheet_trimmed corrects the direction(s) of individual SP-curves which are reversed with respect to the rest, but does not attempt to resolve the correct sequence if curves are input out of order.
SP-curves supplied need not meet their neighbors to within the sum of the edge tolerances. Points for vertices are computed by Parasolid by averaging curve ends, and sensible tolerances deduced. This allows a loop representation in the case of a surface parametric singularity (sphere pole) which does not incorporate a zero length (in 3-space) SP-curve representing the degeneracy. Therefore the user can legitimately supply the following data:

Figure 44-5 Trimmed curves part of whole loop

From this data Parasolid computes vertex point and tolerance:

Figure 44-6 Trimmed curves part of whole loop plus computed vertex and tolerance

P is the average centroid point computed using end of C1 and start of C2. The tolerance is the maximum distance of C1 or C2 away from P.

Note: If C1 and C2 do not follow on to within specified tolerances (as in the case in Figure 44-5) PK_SURF_make_sheet_trimmed does NOT attempt corrective action in the case where C2 is reversed accidentally with respect to C1.

There is no need to represent surface seam-lines or portions thereof, but if these are included in the input loops, PK_SURF_make_sheet_trimmed handles them, provided the correct option is set.
No SP-curve should have a length less than twice the supplied edge tolerance.
SP-curves should not approach within the sum of the edge tolerances of others which do not share a common vertex.

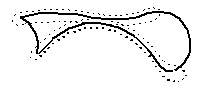
Figure 44-7 SP-curves within edge tolerance of sum of others with no common vertex

Where SP-curves do share a common vertex, the curves should not come within the appropriate edge tolerance sum of one another after separating at the vertex.

Figure 44-8 SP-curves within edge tolerance of sum of others with no common vertex

Neither should SP-curves be entirely within edge tolerance sum of one another.

Figure 44-9 Edge E2 is wholly within E1 tolerance + E2 tolerance of E1

Note: All the configurations in Figs. 8, 9 and 10 can be detected by the means of the checking option


check_self_int

There should be no faces which are wholly within the supplied edge tolerance band. An example of when this can occur is when small faces have been introduced to avoid use of a degenerate B-surface. These faces are not required, nor likewise, are faces which have been created in order to fill slender gaps in the model. Such faces are automatically rejected, and PK_SURF_make_sheet_trimmed returns PK_ENTITY_null.
All intended vertices of the result should correspond to the ends of SP-curves. Loops such as those shown in Figure 44-10 are valid, but prove impossible to knit into composite sheets or solids later. This situation can be resolved by supplying one SP-curve per intended edge in order to tell Parasolid where the vertices of the resultant sheet are to be.

Figure 44-10 Examples of SP-curves and their vertices

PK_SURF_make_sheet_trimmed has several levels of optional checking, which pick up the majority of the problems explained in this section when used. These are as follows:

The identification of wire topologies, e.g. seam lines, ensuring that the correct topology is made in such cases - check_wires .

Note: Opposing and coincident (within tolerance) SP-curves should be supplied wherever wires are required.

To enable the application to pick up self-intersections within the sheet - check_self_int .
Checks that the loops of the face are consistent - check_loops . Some limited corrective action is taken to reverse loops going in the wrong direction, though this is NOT guaranteed to produce a valid sheet.

If all input sheet bodies pass these checks, your application can do one of the following:

Complete the sewing operation using PK_BODY_sew_bodies
Create and apply a knitting pattern using PK_BODY_find_knit_pattern and PK_BODY_apply_knit_pattern.

For details on both of these techniques, see Chapter 36, "Sheet Sewing".

[back to top]

44.4 BREP import route

[back to top]

44.4.1 Sequence of events using BREP import route

[back to top]

44.4.2 Importing topology

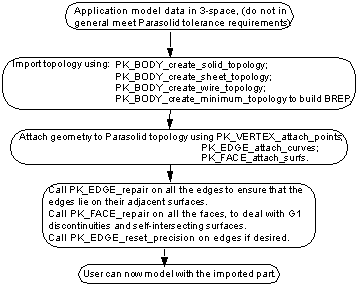
Topology in the Parasolid form is created using one of the functions:

All of these functions take the same arguments which define the topological entities and the relations between them. The topological entities are defined by an array of classes. The allowed classes are:

PK_CLASS_shell
PK_CLASS_face
PK_CLASS_loop
PK_CLASS_edge
PK_CLASS_vertex

The body is made up of all defined shells, the first of which must be the exterior shell.

In relations each topological entity is referred to by its index in the array of classes. Each relation is defined by a parent, a child and a sense. Sense is only meaningful when the parent is of PK_CLASS_loop and the child is of PK_CLASS_edge. Note that every shell defined should be closed, and that this means that open wire and sheet bodies should have additional back faces to form a closed shell. When creating the topology for a wire, PK_BODY_create_wire_topology requires 1 or 2 faces, but these are deleted in the result. However, when creating an open sheet the extra back faces are retained in the result and should be removed using PK_FACE_delete_from_sheet_body.

For further details of the permitted classes and numbers of children and parents for the various body types see the description of the appropriate PK_BODY_create_<body_type>_topology function in the Parasolid PK Programming Reference manual.

The arguments are checked to determine whether they define valid Parasolid topology:

if they do define valid Parasolid topology then a purely topological body is created and an array of created topological entities corresponding to the given array of classes is returned.
if they do not define valid Parasolid topology then a fault code is returned indicating why the specified topology is invalid.

The entities and relations specified in the arguments need to correspond to the model in the external system, although in some cases it may be necessary and possible to add or delete some items; for example, faces without an attached surface on sheets or isolated vertex-loops.

[back to top]

44.4.3 Creating geometry

There is an extensive range of primary geometry functions. The majority of these have names of the form PK_<GEOM>_create, for example:

Geometry	Functions	Geometry	Functions
for points:	PK_POINT_create	for surfaces:	PK_BSURF_create PK_CONE_create PK_CYL_create PK_FSURF_create PK_OFFSET_create PK_PLANE_create PK_SPHERE_create PK_SPUN_create PK_SWEPT_create PK_TORUS_create
for curves:	PK_BCURVE_create PK_CIRCLE_create PK_ELLIPSE_create PK_FCURVE_create PK_LINE_create PK_SPCURVE_create	for surfaces:

B-geometry can also be created from spline data or piecewise data using:

As well as these there is a wide range of functions of the form PK_ <GEOM>_make_ <something> which make geometry from other geometry.

You can simplify geometry using PK_BODY_simplify_geom or PK_FACE_simplify_geom. See Section 40.1, "Simplifying geometry", for more information.

[back to top]

44.4.4 Attaching geometry

To create a valid body, geometry of the correct class must be attached to all of its vertices, edges and faces; these entities having been returned by the appropriate PK_BODY_create_<body_type>_topology function. It is recommended that all geometry be made construction geometry of the body using PK_PART_add_geoms before being attached to particular topological entities.

The geometry should be attached to topology as follows (the order is arbitrary):

points are attached to vertices by PK_VERTEX_attach_points
curves are attached to edges by PK_EDGE_attach_curves
surfaces are attached to faces by PK_FACE_attach_surfs

Care must be taken to ensure that curve directions and surface normal directions are correct. Parasolid conventions regarding curve directions and surface normal directions are described in Chapter 3, "Model Structure". Curve direction may be determined by calling PK_CURVE_eval and reversed by calling PK_CURVE_make_curve_reversed if necessary. Surface normal direction may be determined by calling PK_SURF_eval_with_normal. When a surface is attached to a face using PK_FACE_attach_surfs the application must indicate whether the surface normal is in the same or opposite direction to that of the face normal.

To minimize storage requirements and ensure that SPCurves refer to surfaces attached to faces it is recommended that PK_BODY_share_geom is called once all geometry has been attached.

[back to top]

44.4.5 Repairing the part

After the geometry has been attached, the part may need to be repaired to ensure that Parasolid tolerances are met as follows:

Call PK_EDGE_repair on all the edges. This calculates the maximum distance between the edge curve and its adjacent surfaces. If an edge curve does not lie on its adjacent surfaces, or a vertex does not lie on its adjacent edges, then appropriate tolerances are computed and set on the edge or vertex.
Call PK_FACE_repair on all the faces. This splits the faces along any G1 discontinuities. It also attempts to exclude any regions of surface self-intersection from the face, by splitting the face.

If desired, PK_EDGE_reset_precision may be called on the edges. This attempts to compute accurate edge curves for non-tangent edges by intersecting the adjacent surfaces. Alternatively, the edges may be left with local tolerances.

Examples

Example 1:

To construct the topology of a box

A box can be split into 33 topological entities, these are:

one shell
six faces
six loops
twelve edges
eight vertices

The classes argument to PK_BODY_create_solid_topology is an array of 33 tokens of type PK_class_t.

There are 60 relations, these are:

the one shell is the parent of six faces - 6
each face is the parent of one loop - 6
each loop is the parent of four edges - 24
each edge is the parent of two vertices - 24

With the classes array as:

index	value	index	value
0	PK_CLASS_shell	17	PK_CLASS_edge
1	PK_CLASS_face	18	PK_CLASS_edge
2	PK_CLASS_face	19	PK_CLASS_edge
3	PK_CLASS_face	20	PK_CLASS_vertex
4	PK_CLASS_face	21	PK_CLASS_vertex
5	PK_CLASS_face	22	PK_CLASS_loop
6	PK_CLASS_face	23	PK_CLASS_edge
7	PK_CLASS_loop	24	PK_CLASS_edge
8	PK_CLASS_edge	25	PK_CLASS_vertex
9	PK_CLASS_edge	26	PK_CLASS_loop
10	PK_CLASS_edge	27	PK_CLASS_edge
11	PK_CLASS_edge	28	PK_CLASS_edge
12	PK_CLASS_vertex	29	PK_CLASS_vertex
13	PK_CLASS_vertex	30	PK_CLASS_loop
14	PK_CLASS_vertex	31	PK_CLASS_edge
15	PK_CLASS_vertex	32	PK_CLASS_loop
16	PK_CLASS_loop

Note: Since in this case each face only has a single loop, the loop index is just shown with each face.

The full set of relations is as follows

parents	children	senses	relation
0	1	none	shell to face
0	2	none	shell to face
0	3	none	shell to face
0	4	none	shell to face
0	5	none	shell to face
0	6	none	shell to face
1	7	none	face to loop
7	8	negative	loop to edge
7	9	negative	loop to edge
7	10	negative	loop to edge
7	11	negative	loop to edge
8	12	none	edge to vertex
8	13	none	edge to vertex
9	14	none	edge to vertex
9	12	none	edge to vertex
10	15	none	edge to vertex
10	14	none	edge to vertex
11	13	none	edge to vertex
11	15	none	edge to vertex
2	16	none	face to loop
16	17	positive	loop to edge
16	8	positive	loop to edge
16	18	negative	loop to edge
16	19	positive	loop to edge
17	20	none	edge to vertex
17	12	none	edge to vertex
18	21	none	edge to vertex
18	13	none	edge to vertex
19	21	none	edge to vertex
19	20	none	edge to vertex
3	22	none	face to loop
22	18	positive	loop to edge
22	11	positive	loop to edge
22	23	negative	loop to edge
22	24	positive	loop to edge
23	25	none	edge to vertex
23	15	none	edge to vertex
24	25	none	edge to vertex
24	21	none	edge to vertex
4	26	none	face to loop
26	23	positive	loop to edge
26	10	positive	loop to edge
26	27	negative	loop to edge
26	28	positive	loop to edge
27	29	none	edge to vertex
27	14	none	edge to vertex
28	29	none	edge to vertex
28	25	none	edge to vertex
5	30	none	face to loop
30	31	negative	loop to edge
30	19	negative	loop to edge
30	24	negative	loop to edge
30	28	negative	loop to edge
31	20	none	edge to vertex
31	29	none	edge to vertex
6	32	none	face to loop
32	31	positive	loop to edge
32	27	positive	loop to edge
32	9	positive	loop to edge
32	17	negative	loop to edge

The above information may be passed to either PK_BODY_create_solid_topology or PK_BODY_create_sheet_topology to create either a solid or a closed sheet respectively.

Example 2:

To construct the topology of a cylindrical body

A solid cylinder consists of 10 topological entities. These are:

one shell
three faces
four loops
two edges

The classes argument to PK_BODY_create_solid_topology is an array of 10 tokens of type PK_CLASS_t.

There are 11 relations. These are:

the one shell is the parent of three faces - 3
the planar end faces each have one loop - 2
the cylindrical face has two loops - 2
each loop is the parent of one edge - 3

With the classes array as

index	value	index	value
0	PK_CLASS_shell	5	PK_CLASS_edge
1	PK_CLASS_face	6	PK_CLASS_loop
2	PK_CLASS_face	7	PK_CLASS_edge
3	PK_CLASS_face	8	PK_CLASS_loop
4	PK_CLASS_loop	9	PK_CLASS_loop

The full set of relations is as follows:

parents	children	senses	relation
0	1	none	shell to face
0	2	none	shell to face
0	3	none	shell to face
1	4	none	face to loop
4	5	negative	loop to edge
2	6	none	face to loop
6	7	negative	loop to edge
3	8	none	face to loop
3	9	none	face to loop
8	5	positive	loop to edge
9	7	positive	loop to edge

The above information may be passed to either PK_BODY_create_solid_topology or PK_BODY_create_sheet_topology to create either a solid or a closed sheet respectively.

In KID form, the complete creation of a solid cylinder may be written as:

( setq create_result
  ( pk_body_create_solid_topology
  ´( PK_CLASS_shell PK_CLASS_face PK_CLASS_face PK_CLASS_face
     PK_CLASS_loop PK_CLASS_edge  PK_CLASS_loop PK_CLASS_edge
     PK_CLASS_loop PK_CLASS_loop
   )
  ´( 0 0 0 1 4 2 6 3 3 8 9 )
  ´( 1 2 3 4 5 6 7 8 9 5 7 )
  ´( PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
     PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
     PK_TOPOL_sense_negative_c PK_TOPOL_sense_none_c
     PK_TOPOL_sense_negative_c PK_TOPOL_sense_none_c
     PK_TOPOL_sense_none_c PK_TOPOL_sense_positive_c
     PK_TOPOL_sense_positive_c
    )
  )
)

( setq topols ( element 2 create_result ) )
( setq face_1 ( element 2 topols ) )
( setq face_2 ( element 3 topols ) )
( setq face_3 ( element 4 topols ) )
( setq edge_5 ( element 6 topols ) )
( setq edge_7 ( element 8 topols ) )
( setq plane_1 
    ( pk_plane_create ´( ( (0 0 5) (0 0  1) (1 0 0) ) ) ) )
( setq plane_2 
    ( pk_plane_create ´( ( (0 0 0) (0 0 -1) (1 0 0) ) ) ) )
( setq cyl_3 
    ( pk_cyl_create ´( ( (0 0 0) (0 0  1) (1 0 0) ) 10 ) ) )
( setq circle_5 
    ( pk_circle_create ´( ( (0 0 5) (0 0 -1) (1 0 0) ) 10 ) ) )
( setq circle_7 
    ( pk_circle_create ´( ( (0 0 0) (0 0  1) (1 0 0) ) 10 ) ) )

( pk_edge_attach_curves ( list edge_5   edge_7   )
                        ( list circle_5 circle_7 )
)

( pk_face_attach_surfs ( list face_1  face_2  face_3 )
                       ( list plane_1 plane_2 cyl_3  )
                       ( list t       t       t      )
)

Example 3:

To construct the topology of a conical body

A complete cone with zero radius at one end has different topology to a truncated cone with non-zero radii at each end. The latter has the same topology as a cylinder; in the former there are only two faces, one planar and one conical. One of the loops bounding the conical face is degenerate, containing no edges but just a single vertex.

A complete solid cone consists of 8 topological entities. These are:

one shell
two faces
three loops
one edge
one vertex

The classes argument to PK_BODY_create_solid_topology is an array of 8 tokens of type PK_CLASS_t.

There are 8 relations. These are:

the one shell is the parent of two faces - 2
the planar end face has one loop - 1
the conical face has two loops - 2
two loops are each the parent of one edge - 2
one loop is the parent of a vertex - 1

With the classes array as:

index	value	index	value
0	PK_CLASS_shell	4	PK_CLASS_edge
1	PK_CLASS_face	5	PK_CLASS_loop
2	PK_CLASS_face	6	PK_CLASS_loop
3	PK_CLASS_loop	7	PK_CLASS_vertex

The full set of relations is as follows:

parents	children	senses	relation
0	1	none	shell to face
0	2	none	shell to face
1	3	none	face to loop
3	4	negative	loop to edge
2	5	none	face to loop
2	6	none	face to loop
5	4	positive	loop to edge
6	7	none	loop to vertex

The above information may be passed to either PK_BODY_create_solid_topology or PK_BODY_create_sheet_topology to create either a solid or a closed sheet respectively.

In KID form, the complete creation of a solid cone may be written as:

( setq create_result
  ( pk_body_create_solid_topology
    ´( PK_CLASS_shell PK_CLASS_face PK_CLASS_face PK_CLASS_loop
       PK_CLASS_edge PK_CLASS_loop  
       PK_CLASS_loop PK_CLASS_vertex)
    ´( 0 0 1 3 2 2 5 6 )
    ´( 1 2 3 4 5 6 4 7 )
    ´( PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c
       PK_TOPOL_sense_negative_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_positive_c
       PK_TOPOL_sense_none_c)))

( setq topols ( element 2 create_result ) )
( setq face_1 ( element 2 topols ) )
( setq face_2 ( element 3 topols ) )
( setq edge_4 ( element 5 topols ) )
( setq vertex_7 ( element 8 topols ) )
( setq angle ( quotient pi 6 ) )
( setq plane_1 ( pk_plane_create 
                    ´( ( (0 0 10) (0 0  1) (1 0 0) ) ) ) )
( setq cone_2 
   ( pk_cone_create ( list ´( (0 0  0) (0 0  1) (1 0 0) )
                            0 angle)))

( setq circle_4 ( pk_circle_create 
                   ( list ´( (0 0 10) (0 0 -1) (1 0 0) )
                           ( times 10 ( tan angle ) ))))

( setq point_7 ( pk_point_create ´( ( 0 0 0 ) ) ) )
( pk_vertex_attach_points ( list vertex_7 ) ( list point_7 ) )
( pk_edge_attach_curves ( list edge_4 ) ( list circle_4 ) )
( pk_face_attach_surfs ( list face_1  face_2 )
                       ( list plane_1 cone_2 )
                       ( list t       t      ))

Example 4:

To construct the topology of a spherical or toroidal body.

A spherical and toroidal body have the same topology, consisting of only a shell and a face

A spherical or toroidal body contains 2 topological entities. These are:

one shell
one face

The classes argument to PK_BODY_create_solid_topology is an array of 2 tokens of type PK_CLASS_t.

There is 1 relation:

the one shell is the parent of the one face - 1

The classes array is:

index	value
0	PK_CLASS_shell
1	PK_CLASS_face

The sole relation is:

parents	children	senses	relation
0	1	none	shell to face

The above information may be passed to either PK_BODY_create_solid_topology or PK_BODY_create_sheet_topology to create either a solid or a closed sheet respectively.

To complete the body a sphere or torus must be attached to the single face.

Example 5:

To construct the topology of a circular sheet

Sheet bodies must be defined with faces on both sides although the unused faces must be deleted before geometry is attached.

A circular sheet contains 6 topological entities. These are:

one shell
two faces
two loops
one edge

The classes argument to PK_BODY_create_sheet_topology is an array of 6 tokens of type PK_CLASS_t.

There are 6 relations:

the one shell is the parent of the two faces - 2
each face is the parent of one loop - 2
each loop is the parent of the one edge - 2

The classes array is:

index	value
0	PK_CLASS_shell
1	PK_CLASS_face
2	PK_CLASS_face
3	PK_CLASS_loop
4	PK_CLASS_loop
5	PK_CLASS_edge

The relations are:

parents	children	senses	relation
0	1	none	shell to face
0	2	none	shell to face
1	3	none	face to loop
2	4	none	face to loop
3	5	positive	loop to edge
4	5	negative	loop to edge

Before any geometry is attached to the body, the unused face must be removed using PK_FACE_delete_from_sheet_body.

In KID form, the complete creation of a circular sheet may be written as:

( setq create_result
  ( pk_body_create_sheet_topology
    ´( PK_CLASS_shell PK_CLASS_face PK_CLASS_face PK_CLASS_loop
       PK_CLASS_loop PK_CLASS_edge)
    ´( 0 0 1 2 3 4 )
    ´( 1 2 3 4 5 5 )
    ´( PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_positive_c PK_TOPOL_sense_negative_c)))

( setq topols ( element 2 create_result ) )
( setq face_1 ( element 2 topols ) )
( setq face_2 ( element 3 topols ) )
( setq edge_5 ( element 6 topols ) )
( setq plane_1 ( pk_plane_create 
                    ´( ( (0 0 0) (0 0  1) (1 0 0) ) ) ) )
( setq circle_5 ( pk_circle_create 
                    ´( ( (0 0 0) (0 0 1) (1 0 0) ) 10 ) ) )
( pk_face_delete_from_sheet_body face_2 )
( pk_edge_attach_curves ( list edge_5 ) ( list circle_5 ) )
( pk_face_attach_surfs 
     ( list face_1 ) ( list plane_1 ) ( list t ) )

Example 6:

To construct the topology of a circular wire

Wire topology is defined with a single face. If the wire is closed then the face has two loops which run in opposite directions around the wire.

A circular wire contains 5 topological entities. These are:

one shell
one face
two loops
one edge

The classes argument to PK_BODY_create_wire_topology is an array of 5

tokens of type PK_CLASS_t.

There are 5 relations:

the one shell is the parent of one face - 1
each face is the parent of two loops - 2
each loop is the parent of the one edge - 2

The classes array is:

index	value
0	PK_CLASS_shell
1	PK_CLASS_face
2	PK_CLASS_loop
3	PK_CLASS_loop
4	PK_CLASS_edge

The relations are:

parents	children	senses	relation
0	1	none	shell to face
1	2	none	face to loop
1	3	none	face to loop
2	4	positive	loop to edge
3	4	negative	loop to edge

The body created by PK_BODY_create_wire_topology has no face or loops. The returned topols corresponding to these classes are set to PK_ENTITY_null.

In KID form, the complete creation of a circular sheet may be written as:

( setq create_result
  ( pk_body_create_wire_topology
    ´( PK_CLASS_shell PK_CLASS_face PK_CLASS_loop PK_CLASS_loop
       PK_CLASS_edge )
    ´( 0 1 1 2 3 )
    ´( 1 2 3 4 4 )
    ´( PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_positive_c
       PK_TOPOL_sense_negative_c)))

( setq topols ( element 2 create_result ) )
( setq edge_4 ( element 5 topols ) )
( setq circle_4 ( pk_circle_create
                    ´( ( (0 0 0) (0 0 1) (1 0 0) ) 10 ) ) )
( pk_edge_attach_curves ( list edge_4 ) ( list circle_4 ) )

Example 7:

To construct the topology of a linear wire

Wire topology is defined with a single face. If the wire is open then there is a single loop which runs from one end of the loop to the other and back again.

A linear wire contains 6 topological entities. These are:

one shell
one face
one loop
one edge
two vertices

The classes argument to PK_BODY_create_wire_topology is an array of 6 tokens of type PK_CLASS_t.

There are 6 relations:

the one shell is the parent of one face - 1
the face is the parent of one loop - 1
the loop is the parent of the one edge in each direction - 2
the edge is the parent of two vertices

The classes array is:

index	value	index	value
0	PK_CLASS_shell	3	PK_CLASS_edge
1	PK_CLASS_face	4	PK_CLASS_vertex
2	PK_CLASS_loop	5	PK_CLASS_vertex

The relations are:

parents	children	senses	relation
0	1	none	shell to face
1	2	none	face to loop
2	3	positive	loop to edge
2	3	negative	loop to edge
3	4	none	edge to vertex
3	5	none	edge to vertex

The body created by PK_BODY_create_wire_topology has no face or loop. The returned topols corresponding to these classes are set to PK_ENTITY_null.

Example 8:

To construct the topology of a tetrahedron

A tetrahedron has 19 topological entities. These are:

one shell
four faces
four loops
six edges
four vertices

The classes argument to PK_BODY_create_solid_topology is an array of 19 tokens of type PK_CLASS_t.

There are 32 relations. These are:

the one shell is the parent of four faces - 4
each face is the parent of one loop - 4
each loop is the parent of three edges - 12
each edge is the parent of two vertices - 12

With the classes array as:

index	value	index	value
0	PK_CLASS_shell	10	PK_CLASS_edge
1	PK_CLASS_face	11	PK_CLASS_edge
2	PK_CLASS_face	12	PK_CLASS_edge
3	PK_CLASS_face	13	PK_CLASS_edge
4	PK_CLASS_face	14	PK_CLASS_edge
5	PK_CLASS_loop	15	PK_CLASS_vertex
6	PK_CLASS_loop	16	PK_CLASS_vertex
7	PK_CLASS_loop	17	PK_CLASS_vertex
8	PK_CLASS_loop	18	PK_CLASS_vertex
9	PK_CLASS_edge

Note: Since in this case each face only has a single loop, the loop index is just shown with each face.

The full set of relations is as follows:

parents	children	senses	relation
0	1	none	shell to face
0	2	none	shell to face
0	3	none	shell to face
0	4	none	shell to face
1	5	none	face to loop
2	6	none	face to loop
3	7	none	face to loop
4	8	none	face to loop
5	9	positive	loop to edge
5	10	positive	loop to edge
5	11	positive	loop to edge
6	9	negative	loop to edge
6	14	positive	loop to edge
6	12	negative	loop to edge
7	10	negative	loop to edge
7	12	positive	loop to edge
7	13	negative	loop to edge
8	11	negative	loop to edge
8	13	positive	loop to edge
8	14	negative	loop to edge
9	15	none	edge to vertex
9	16	none	edge to vertex
10	16	none	edge to vertex
10	17	none	edge to vertex
11	17	none	edge to vertex
11	16	none	edge to vertex
12	16	none	edge to vertex
12	18	none	edge to vertex
13	17	none	edge to vertex
13	18	none	edge to vertex
14	15	none	edge to vertex
14	18	none	edge to vertex

The above information may be passed to either PK_BODY_create_solid_topology or PK_BODY_create_sheet_topology to create either a solid or a closed sheet respectively.

In KID form, the complete creation of a solid tetrahedron may be written as:

( setq create_result
  ( pk_body_create_solid_topology
    ´( PK_CLASS_shell PK_CLASS_face PK_CLASS_face PK_CLASS_face
       PK_CLASS_face PK_CLASS_loop PK_CLASS_loop PK_CLASS_loop
       PK_CLASS_loop PK_CLASS_edge PK_CLASS_edge PK_CLASS_edge
       PK_CLASS_edge PK_CLASS_edge PK_CLASS_edge PK_CLASS_vertex
       PK_CLASS_vertex PK_CLASS_vertex PK_CLASS_vertex)
    ´(  0  0  0  0  1  2  3  4  5  5  5  6  6  6  7  7  7  
        8  8  8  9  9 10 10 11 11 12 12 13 13 14 14)
    ´(  1  2  3  4  5  6  7  8  9 10 11  9 14 12 10 12 13 11 
        13 14 15 16 16 17 17 15 16 18 17 18 15 18)
    ´( PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_positive_c PK_TOPOL_sense_positive_c
       PK_TOPOL_sense_positive_c PK_TOPOL_sense_negative_c
       PK_TOPOL_sense_positive_c PK_TOPOL_sense_negative_c
       PK_TOPOL_sense_negative_c PK_TOPOL_sense_positive_c
       PK_TOPOL_sense_negative_c PK_TOPOL_sense_negative_c
       PK_TOPOL_sense_positive_c PK_TOPOL_sense_negative_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c
       PK_TOPOL_sense_none_c PK_TOPOL_sense_none_c)))

( setq topols ( element  2 create_result ) )
( setq face_1 ( element  2 topols ) )
( setq face_2 ( element  3 topols ) )
( setq face_3 ( element  4 topols ) )
( setq face_4 ( element  5 topols ) )
( setq edge_9 ( element 10 topols ) )
( setq edge_10 ( element 11 topols ) )
( setq edge_11 ( element 12 topols ) )
( setq edge_12 ( element 13 topols ) )
( setq edge_13 ( element 14 topols ) )
( setq edge_14 ( element 15 topols ) )
( setq vertex_15 ( element 16 topols ) )
( setq vertex_16 ( element 17 topols ) )
( setq vertex_17 ( element 18 topols ) )
( setq vertex_18 ( element 19 topols ) )
( setq line_9 ( pk_line_create ´( ( (0 0 0) (1 0 0) ) ) ) )

( setq line_10 
 ( pk_line_create ´( ( (1 0 0) (-0.707106781187 0.707106781187 0)
))))

( setq line_11 ( pk_line_create ´( ( (0 1 0) (0 -1 0) ) ) ) )
( setq line_12 
 ( pk_line_create ´( ( (1 0 0) (-0.707106781187 0 0.707106781187)
))))

( setq line_13 
 ( pk_line_create ´( ( (0 1 0) (0 -0.707106781187 0.707106781187)
))))

( setq line_14 ( pk_line_create ´( ( (0 0 0) (0 0 1) ) ) ) )
( setq point_15 ( pk_point_create ´( (0 0 0) ) ) )
( setq point_16 ( pk_point_create ´( (1 0 0) ) ) )
( setq point_17 ( pk_point_create ´( (0 1 0) ) ) )
( setq point_18 ( pk_point_create ´( (0 0 1) ) ) )

( pk_vertex_attach_points 
   ( list vertex_15 vertex_16 vertex_17 vertex_18 )
   ( list point_15 point_16 point_17 point_18 )

( pk_edge_attach_curves 
   ( list edge_9 edge_10 edge_11 edge_12 edge_13 edge_14 )
   ( list line_9 line_10 line_11 line_12 line_13 line_14 )

( pk_face_attach_surf_fitting face_1 nil )
( pk_face_attach_surf_fitting face_2 nil )
( pk_face_attach_surf_fitting face_3 nil )
( pk_face_attach_surf_fitting face_4 nil )

[back to top]

44.5 Relevant Parasolid restrictions and conventions

[back to top]

44.5.1 Face normals

By convention, in Parasolid all face normals point out of the material of the body, for faces bounding voids this means into the void. Face normals are determined by:

the normal of the surface attached to the face;
the sense of the face.

The sense of a face is set by the senses argument to PK_FACE_attach_surfs:

If the sense argument is set to PK_LOGICAL_true the face normal is parallel to the surface normal.
If it is set to PK_LOGICAL_false it is anti-parallel.

[back to top]

44.5.2 Loop directions and faces

In Parasolid, the face of a loop is on its left, when looking from outside the material of the body and moving in the loop direction.

If the modeler from which a body is being imported has the opposite convention, all loop directions need to be reversed. This is done by either:

switching all edge senses as given in the senses argument received by PK_BODY_create_solid_topology;
reversing curve directions, by for example, using PK_BODY_reverse_orientation, in the case of bodies with curves on edges. Care must be taken that points are attached to vertices consistently with the direction of the loop. PK_BODY_reverse_orientation must be called on the whole body for sheets with fin geometry.

[back to top]

44.5.3 Non-manifold bodies

All Parasolid bodies that are created in a session where PK_SESSION_set_general_topology has not been run must be manifold, objects such as T-sheets or solid regions meeting at a point are not permitted.

For further information on manifold bodies and generalized topology, see Chapter 6, "Manifold Bodies" and Chapter 7, "General Bodies".

[back to top]

44.5.4 B-curves and edges

The B-curve of an edge must be G1 continuous. It can have multi-segments so long as it is G1 continuous. If a B-curve is not G1 continuous it needs to be split at the G1 discontinuities, each of which can be attached to a separate edge.

[back to top]

44.6 Data import mending

Note: The following method for mending imported data has been retained as backup to the method previously explained in this chapter and for clarity/compatibility with the v4.0 documentation and is only available through the Kernel Interface (KI) routine MENDEN.

Models that have been imported into Parasolid may not satisfy Parasolid's requirements for accuracy and consistency between topology and geometry. Such models may be mended to Parasolid precision using the KI routine MENDEN.

MENDEN accepts imported bodies and attempt to recalculate edge and vertex geometries to Parasolid tolerance. In doing so, use is made of the user-specified geometry originally attached to the model, so success depends to some extent on the accuracy of the initial data. It is also assumed that during construction of the imported model, surfaces have been attached to faces with the correct sense, and that curves have been attached to edges or fins in the correct direction.

If the recalculation of edge and vertex geometry is successful, MENDEN negates shells of the body if this is necessary.

MENDEN returns a token to indicate whether or not all edge and vertex geometry has been successfully recalculated. If it has, this means only that the body is accurate to Parasolid tolerance; not that it is a valid body. A successful call to MENDEN should therefore always be followed by a call to PK_BODY_check.

If MENDEN does not succeed in recalculating all the edges and vertex geometry, lists containing the tags of the faulty edges and vertices together with lists of tokens indicating the reason for failure are returned. Using this information a second attempt at mending the model can be made by replacing geometry in the vicinity of the faulty edges and vertices. The complete body, or just an appropriate list of edges can then be supplied to MENDEN again. If the latter is supplied, care must be taken to include:

all faulty edges;
edges whose geometry has been changed since the previous call to MENDEN;
edges meeting at all faulty vertices;
all edges in a face whose surface has been replaced.

If MENDEN does not successfully recalculate all edge and vertex geometry, the body remains user-specified and only limited functionality is available to it.

[back to top]

44.6.1 Limitations of the mending process

The mending process is designed to tighten up models to Parasolid tolerance so that full Parasolid functionality is available to them. Success however is not guaranteed, and there are certain conditions under which the mending process is likely or certain to fail.

Failure is certain for:

Trimmed surface sheet bodies;
Bodies which have faces without attached geometry.

Failure is likely for:

BREP sheet bodies, especially if faces are non-planar;
Bodies containing vertices where more than four edges meet;
Bodies with edges where adjacent surfaces meet tangentially, or nearly tangentially.

The limitations on sheet bodies arise due to problems projecting curves onto surfaces. This occurs in other situations as well, for example, if the surfaces adjacent to an edge of the body are coincident. Near tangencies are problematic for different reasons, as described in the following examples.

Example 1

A model consisting of a cylinder topped by a hemisphere of approximately equal radius.

Figure 44-11 Cylinder topped by a hemisphere

If the sphere is slightly too small, the spherical and cylindrical surfaces may not intersect within Parasolid tolerance, so that no replacement curve can be calculated for the edge adjacent to these surfaces. This edge consequently appears in the list of faulty edges returned by MENDEN.

Example 2

Two cylinders with approximately parallel axes and equal radii joined end to end, with a circular ring edge at the join.

Figure 44-12 Two cylinders end to end with approximately parallel axes

If the axes of the cylinders are not sufficiently in alignment to be considered by Parasolid as parallel, the intersection of the two cylindrical surfaces produces a set of semi-ellipses rather than a circle. The supplied topology is then inadequate and again the edge fails to mend.

There are also limitations on the amount of missing geometry that MENDEN allows. If there is insufficient geometry on a model, the mending process does not begin and MENDEN simply returns an error. The following rules apply:

Any number of faces without attached geometry are allowed, but as indicated above, the presence of these faces reduces the chance of a successful mend.
All edges must either have a curve attached directly to them, or have an SP-curve attached to at least one of their fins.
All vertices must have a point, unless at least one fin meeting at the vertex has an SP-curve attached.

These restrictions apply whether the whole body or just a list of edges from a body are supplied to MENDEN.

A further limitation of the mending process is that it assumes that the direction of curves and surface senses are correct. If any curves or surfaces have been attached wrongly, so that edge directions and face normals are inconsistent, mending proceeds regardless. However, even if the mend is successful, the resulting body is invalid and fails the checks imposed by PK_BODY_check.

[back to top]

<<< Assemblies and Instances

Chapters

Groups >>>

Contents

44.1 Introduction

44.2 Trimmed surface import route - summary

44.3 Requirements for data import using the trimmed surface import route

44.3.1 SP-curve data

Introduction

Criteria

44.3.2 DOC0276Trimmed surface data passed into PK_SURF_make_sheet_trimmed

Introduction

Criteria

44.4 BREP import route

44.4.1 Sequence of events using BREP import route

44.4.2 Importing topology

44.4.3 Creating geometry

44.4.4 Attaching geometry

44.4.5 Repairing the part

Examples

Example 1:

Example 2:

Example 3:

Example 4:

Example 5:

Example 6:

Example 7:

Example 8:

44.5 Relevant Parasolid restrictions and conventions

44.5.1 Face normals

44.5.2 Loop directions and faces

44.5.3 Non-manifold bodies

44.5.4 B-curves and edges

44.6 Data import mending

44.6.1 Limitations of the mending process

Example 1

Example 2