 |
Manifold Bodies |
| <<< Nominal Geometry | Chapters | General Bodies >>> |
General bodies are described in detail in Chapter 7, "General Bodies".
There are four stages of manifold body, increasing in topological complexity. These are known as acorn, wire, sheet and solid bodies. The definitions given in this section are the definitions of completely specified bodies of each type. It is possible to make bodies which are not complete geometrically. Such bodies are said to have missing geometry.
Creation of a solid might frequently progress through the body types. Beginning with a minimum or acorn body, scribing lines onto it turns it into a wire body. Closing the profile with a final scribe and adding a surface turns the wire into a sheet. The sheet could then be swept or spun to form a solid. The details of these processes are explained later on in this chapter.
The entities which make up the manifold body types are described in the following sections, along with any restrictions that apply. In addition, note that manifold bodies can be disjoint and need not be connected: void regions can have several shells. See Section 6.3, "Disjoint solids" for more information.
This is the simplest type of body: a body of zero dimensions comprising one or more points in space. If an acorn body has only one point, then it is a minimum body, as described below. If it has several points, then it is disjoint.
An acorn body contains only one type of geometry - points that are attached to the vertices in the body.
A minimum body is a special case of an acorn body that must consist of a single void region with a single shell consisting of a single acorn vertex.
A wire body is one step up from a minimum body - considered to be topologically one-dimensional. Each component in a wire body is a set of connected edges:
A wire body must consist of a single void region, with a single shell for each component. Each shell has one or more wireframe edges and zero or more vertices (and no faces). Every vertex in the body must be used by exactly one or two of the edges, i.e. there are no acorn vertices.
Given the connectedness constraint, this means that every component in the body is one of:
A sheet body is considered to be topologically two-dimensional. Each component in a sheet body is either open (e.g. a bounded plane) or closed (e.g. a hollow sphere or torus whose walls have zero thickness).
Each component in a sheet body must contain at least one face. A component may be open or closed (bounds a volume, such as a cube created from faces) Sheet bodies may not contain any wireframe edges or acorn vertices.
Sheet bodies have no solid regions. A sheet body that contains only open components has one infinite void region containing any number of shells, each of which contains a single set of connected faces. For each closed set of connected faces in a sheet body, there is an extra bounded void region representing the interior of the closed set of connected faces.
Every edge in a sheet body must be one of:
Every vertex in a sheet body must either belong to a single isolated loop, or belong to one or more edges. In the latter case, either all the edges of the vertex must be normal and the faces which use those edges must form a single edgewise-connected set (see Figure 6-1), or there can be one (Figure 6-2) or more (Figure 6-3) edgewise-connected sets, each of which must involve exactly two laminar edges and any number of normal edges.

Figure 6-1 Vertices in open sheet bodies - one faceset, all edges are normal

Figure 6-2 Vertices in open sheet bodies - one faceset, one normal and two laminar edges

Figure 6-3 Valid (non-manifold) vertex in an open sheet body - two facesets
A solid body is three-dimensional, and occupies a finite volume. The volume of each component in a solid body is continuous.
The following restrictions apply to solid bodies:
|
Note: These constraints ensure that the solid is
manifold. |
Disconnected pieces can remain in a single manifold body, facilitating data tracking in a feature modeler. For example, Figure 6-4 shows the result of subtracting a cylinder from a block.

Figure 6-4 General body consisting of four disconnected pieces
There are four ways to create a manifold body:
When a body of any sort is created, all the other entities which are required (i.e. any necessary faces, edges etc.) are created with it. For example, PK_POINT_make_minimum_body creates a minimum body containing one shell and one vertex with the given point attached.
The primitives are sometimes also referred to as analytic bodies. These functions automatically generate all the topology and geometry required for these bodies.
The PK functions available to create a primitive body are:
| Functions to create sheets | Functions to create solids |
|---|---|
The position of the new body is based on the origin, either in the local coordinate system if required, or the world coordinate system.
The world coordinate system is the coordinate system in which the size box is defined:
The local coordinate system is used to define an entity in a convenient coordinate system and then separately show how that entity is positioned and oriented in the world coordinate system.
For example, in its local coordinate system a circle lies in the XY plane, has its centre at (0, 0, 0) and has its parametric seam where the circle crosses the X axis. However, a circle that is part of a model may have any position and orientation in the world coordinate system. PK_CIRCLE_ask returns the circle's definition in its local coordinate system (just a radius) and a
basis_set
which gives the position and orientation of the local coordinate system in the world coordinate system.
The local coordinate system of a new body is defined by passing an axis to the creating function, using a PK_AXIS2_sf_t structure. This parameter is optional - if supplied as NULL, it defaults to the world coordinate system.
For all spun geometry (circle, cone, cylinder, sphere, torus) the periodic parameterization has its seam on the positive local X axis. Where the surface has any edges, this also applies to the curves attached to those edges.
You can create apple and lemon tori, such as those shown in Figure 6-5, using PK_BODY_create_solid_torus.
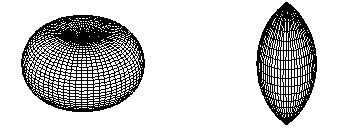
Figure 6-5 Apple and lemon tori
To create an apple or lemon torus, the minor radius must be larger in magnitude than the major radius: if the major radius is positive, an apple is created, and if the major radius is negative, a lemon is created.
The PK functions available to create a body from existing geometry are:
While the parameterization of the geometry used to define the body survives, the parameterization of extra geometry that has to be created (e.g. circular edges of cylindrical solids) cannot be predicted.
In addition to the above functions, PK_BODY_create_sheet_planar can be used to create a planar sheet body whose boundary is an irregular polygon, specified by its vertices. Irregular polygonal holes in the sheet body can also be defined.
If there is no existing geometry to copy, the following PK functions are available for creating orphan geometry:
Points, curves and surfaces created as orphan geometry can also be used to attach construction geometry to a part using PK_PART_add_geoms. PK_PART_ask_geoms returns the geometric entities attached to a part in this way.
This could be used, for example, to create a point which represents the center of gravity of a body, and enable it to be saved with the body.
The following local operations create a body from existing topology:
|
Creates a sheet body from faces in an existing manifold or non-manifold body. |
|
|
Creates solid bodies from faces in an existing manifold body. |
A body can be created by taking a copy of another manifold body, using PK_ENTITY_copy.
The manifold components of a general body can be extracted into individual manifold bodies using PK_BODY_make_manifold_bodies. This could be used, for example, when a boolean operation has returned a general body containing manifold components.
See "Extracting manifold bodies from a general body" in Chapter 7, "General Bodies", for further information on the use of PK_BODY_make_manifold_bodies.
The following operations can be used to generate a particular type of body, by operating on a body which is topologically less complex.
These operations are performed by the set of functions PK_<ENTITY>_sweep and PK_<ENTITY>_spin, which change the type of the body. There is a table of the types of object that can be swept and spun in the full descriptions of these functions, in summary:
When a sheet body has been swept or partially spun the entire sheet body is transformed; a negated copy is made, and connected to it by lateral edges and faces. Therefore the original faces, edges, vertices and geometry of the sheet end up in the transformed position.
Figure 6-6 Entity position after sweeping or partially spinning a sheet body
|
Note: Care must be taken with the positioning of the axis when spinning bodies.For example, it is not permitted to spin a wire body through 2pi if an internal vertex rests on the axis as this would result in a non-manifold sheet body. It is also easy to create self-intersecting bodies by sweeping or spinning. Always check the results, either by having local checking on, or using PK_BODY_check on the resulting bodies. For more information about these restrictions, see the description of the spin functions. |
The imprinting functions PK_BODY_imprint_curve, PK_FACE_imprint_curve, and PK_REGION_imprint_curve are geometric functions that have two major uses:
These two uses are very similar: in general you imprint lines onto the appropriate entity creating new edges by doing so:
When the profile becomes closed, the behavior depends on the generalized topology session parameter (see Chapter 7, "General Bodies"):
A curve that is imprinted onto a face producing more than one edge implicitly results in the sharing of the curve by the edges. Similarly, an edge that splits a face into two or more pieces results in the surface of the original face being shared by all of the new faces.
PK_BODY_thicken thickens a sheet body into a solid body. Refer to "Thickening a sheet body" in Chapter 35, "Sheet Modeling", for further information about thickening.
PK_REGION_make_solid can be used to convert a closed sheet body into a solid body.
Conversely, PK_REGION_make_void converts a single solid body (with no interior voids) into a sheet body.
PK_EDGE_make_faces_from_wire can be used to attach rubber faces (faces with no geometry) to loops of wireframe edges in a wire body, thereby creating a sheet body. This is explained further in the section on "Creating faces to fit wire bodies" in Chapter 37, "Wire Modeling".
PK_FACE_delete_from_sheet_body can be used to create a solid with holes through it from a profile. For example, if a planar sheet body has closed loops of edges imprinted on it, the edges actually bound faces which have the same surface as the plane. PK_FACE_delete_from_sheet_body removes a face bounded by a loop of edges, leaving a hole. Then when the sheet is swept, any pierced holes go right through the solid. For example:
If face 'b' pierces face 'a' before sweeping the result is a solid with a hole:
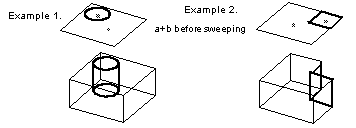
Figure 6-7 Piercing a face before sweeping
If the body in Figure 6-7, Example 1 is swept without piercing, the following solid is returned:
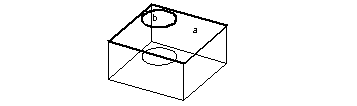
Figure 6-8 Sweeping a sheet body without piercing
In Figure 6-8, the two circles on the top and bottom are edges of faces, but there is no hole. If PK_TOPOL_delete_redundant is used on this body the circular faces and edges are deleted.
In the case of a sheet body with only one face, the result of the piercing operation is either a wire or minimum body; with none of the body's edges and vertices being deleted.
When the body has more than one face, it remains a sheet body after the piercing operation; with edges and vertices belonging to the face, and not shared with other faces, being deleted along with the piercing face.
| <<< Nominal Geometry | Chapters | General Bodies >>> |