 |
Groups |
| <<< Data Import | Chapters | Attribute Definitions >>> |
Each group belongs to a particular part and has a particular class. A group can only contain entities that belong to the same part as the group belongs to. The group class, from the following list, determines the class of entities the groups can contain:
Specifying a single class prevents inappropriate entities being added to the group.
Any number of groups can belong to the same part, and these can be of the same or different classes. Similarly, a particular entity can be in any number of groups that are able to contain that entity.
Groups are entities, and so all the general functions for managing entities can be used on groups.
| Function | Description |
|---|---|
If a number of entities are merged, they are removed from any groups. One occurrence of the resulting entity is added to all groups that contained any of the original entities.
Merging may be performed explicitly or as part of a local operation.
If an entity is split into a number of entities, the new entities are added to any group in which the original entity occurs.
If an entity is deleted, it is removed from any group in which it occurs. If the last entity is removed from the group, the empty group continues to exist.
If a new entity is created other than by splitting an existing entity, the new entity does not occur in any groups as a result of the creation operation.
If a number of bodies are combined by a Boolean operation, the resulting body inherits all the groups of the original bodies.
Entities that are deleted as a result of the merge are removed from the groups. If all the entities in a group are deleted the empty group is still inherited by the resulting body.
Groups are not merged so the resulting body can have two or more groups of the same class.
If a body is split, one of the resulting bodies inherits every group in the original body. The remaining bodies inherit copies of all those groups. If any of the resulting groups contain no entities, then those groups are deleted. A group can only contain entities that belong to the same part, so the contents of each group are modified to remove any entities not in the same part.
In each of the following examples, the block has two groups:
Similarly, the rod has two groups:
Unless stated otherwise, the two bodies are positioned so that their centroids coincide.
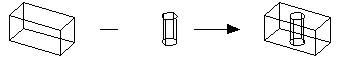
The block and the rod are of identical height and so the resulting body has four groups:

The rod is higher than the block and so the resulting body has three groups:
There is no group 4 because the circular edges are not derived from the edges of the rod.
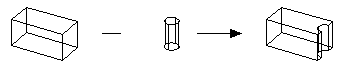
The block and the rod are of identical height and the centroid of the rod is positioned at the center of the block's end face. The resulting body has four groups:

The rod is higher than the block and the centroid of the rod is positioned at the center of the block's end face. The resulting body has three groups:
There is no group 4 because the circular edges are not derived from the edges of the rod.

The rod is higher than the block and so the resulting body has four groups:
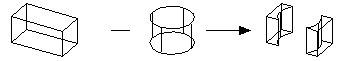
The block and the rod are of identical height and so two bodies are created in the result. Each of the resulting bodies has four groups, as follows:
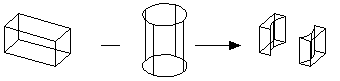
The rod is higher than the block and so the resulting bodies each have three groups:
There is no group 4 because the circular edges are not derived from the edges of the rod.
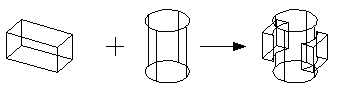
The rod is higher than the block and so the resulting body has four groups:
| <<< Data Import | Chapters | Attribute Definitions >>> |