 |
Session and Local Precision |
| <<< Model Structure | Chapters | Nominal Geometry >>> |
This chapter tells you about the accuracy to which Parasolid models. In particular, it describes:
The linear precision of the modeler. Distances less than this value are treated as zero and distances that differ by no more than this value are treated as equal. The session precision is returned by PK_SESSION_ask_precision.
The smallest angle (in radians) that is treated as different from zero. Angles less than this value are treated as zero and angles that differ by no more than this value are treated as equal. The session angle precision is returned by PK_SESSION_ask_angle_precision.
A Parasolid model is very precise; typically points are not considered coincident unless they are less than 1.0e-8 units apart (linear precision). Also, directions are considered to be parallel if they differ by less than 1.0e-11 units. It is important that data passed to Parasolid is at least this accurate.
To allow precision to be handled correctly, all parts of a body must be within a box (called the size box) whose size is 1000 by 1000 by 1000, and is centered at the origin, as shown in Figure 4-1. You are highly recommended to set the default unit in your application code to one meter, giving 1 kilometer as the maximum distance, in any one direction, that can be modeled.
To handle the precision of arcs correctly, the radius used when creating an arc must be less than a factor of 10 times the dimension of the size box.

Figure 4-1 Linear and angular precision
If possible, we recommend that you do not use models with geometry dimensions at or near to the linear and angular precisions, in order to enhance the reliability of your models. You should try to make sure that:
Sections 4.2.1 to 4.2.4 discuss some difficult precision issues.
For a body to be valid, linear precision must be transitive. Figure 4-2, for example, shows three points for which this is not the case. The distance between points 1 and 2 and points 1 and 3 is such that Parasolid would consider them coincident. However, the distance between points 2 and 3 infers that they are not. Such a body would be declared invalid.

In Figure 4-3, points 'b1' and 'b2' lie on both curves, but if distance 'a' is not greater than Parasolid's linear precision, Parasolid returns the intersection at 'x'.

Figure 4-3 Tangent intersection of two curves
If angle 'a' is less than the angular precision of Parasolid, line 'b1' and the axis are returned as parallel. Subsequently spinning the line from 'x' to 'y' about the axis (the shaded area) creates a cylindrical surface, not a conical surface.

Figure 4-4 A cone that is too 'sharp' to be defined in Parasolid
You may sometimes want to scale parts that have been imported from other modelers, usually as a modeling operation. This may be necessary in order to ensure that the imported parts conform to Parasolid's requirements for precision. However, scaling needs to be performed carefully, for the following reasons:
Modest scaling, up to a factor of 2, is unlikely to cause any problems.
Parts created by other modelers can be imported into Parasolid (as described in Chapter 44, "Data Import") and used in modeling operations. However, such parts were probably created in a modeler that uses a lower precision. Once imported, they may contain inconsistencies between their topological and geometric data: edges which, topologically, should meet at a common point have attached geometric data that does not intersect.
To enable Parasolid to model successfully with imported parts, you can set a local precision on the edges and vertices of any externally created part that contains such inconsistencies. Setting local precision in this way is known as Tolerant Modeling.
When setting local precision, think of edges as tubes, and vertices as spheres. The lower the precision, the thicker the tube or the larger the diameter of the sphere. To use Tolerant Modeling effectively, you need to examine the topology for each part, and, where there is inconsistency in the data, increase the local precision (make the tubes fatter and the spheres bigger) until the geometric data intersects. This can be done with a function such as PK_EDGE_repair, or any of the checking functionality described in Chapter 8, "Checking".
The precision value is stored as a parameter associated with an edge or vertex. It represents the minimum distance (in 3-space) that a point and an entity must be apart in order to be distinct.
|
Note: Your application should consider the use of local precisions a modeling operation, since it can affect both the topology and the geometry of a model. |
Edges and vertices which don't have a local precision set are considered exact by Parasolid, and have a precision of one half of the session precision.
The following subsections describe:
The result of setting precision on an edge depends on whether the edge has already had its precision changed. There are four possible scenarios:
You usually set local precision using PK_EDGE_repair, which can set an appropriate precision for you automatically. Alternatively, you can use PK_EDGE_set_precision to set local precision on an edge. PK_EDGE_ask_precision returns the current precision for an edge.
In Figure 4-5, edge E1 (which has Parasolid session precision) is attached to a number of other edges at vertices V1 and V2.

Figure 4-5 Initial configuration - all edges and vertices are exact
Suppose that local precision is applied to E1 using PK_EDGE_set_precision . Once local precision is set, the following apply (see Figure 4-6 below):
|
Note: It is important to note this difference of geometric representation between edges with and without local precision set. |
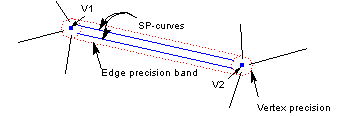
Figure 4-6 Final configuration after precision has been set
For more information about nominal geometry, see Chapter 5, "Nominal Geometry".
Sometimes, it is not possible to compute a single SP-curve from the original curve and the relevant face surface. This is usually due to G1 discontinuities in the surface parameter space, where it is necessary to split the curve and introduce extra vertices on the edge. In such cases, the edge is split a number of times, once for every surface singularity or discontinuity on the original curve. SP-curves are then computed for every relevant fin on the new edges.
Figure 4-7 shows a simple ring edge passing through the poles of a sphere. There are two curves, split at the parameter singularities, which both have local precision set.
|
Note: If you use a function such as PK_EDGE_repair to set local precision, then edges are split for you automatically. |

Figure 4-7 Involving edge splitting
To set local precision correctly, the edge is split into two and SP-curves attached to the relevant fins. Any edges created by this means are returned in a list.
The fins of edge E1 have coincident and reversed SP-curves attached (single segment linear SP-curves in this example, though more generally they would be quadratic B-splines).
If you want to set the local precision of an edge to a different value, the precision of the edge is simply set to the supplied value, and the existing SP-curves are not replaced, even if the precision value supplied is numerically smaller. The precision of any vertices of the edge is set to the supplied value if this is greater than the value already stored there, otherwise, they are left alone. Figure 4-8 shows the effect of resetting edge precision for the edge shown in Figure 4-6.

Figure 4-8 Resetting edge precision to (a) a smaller value (b) a larger value
You can use PK_EDGE_reset_precision to remove local precision from an edge, so that it is once more represented geometrically by an unbounded 3-space curve. In order to recreate this curve, Parasolid removes the SP-curves attached to the underlying edge, and computes the position of the new curve by finding the intersection of the underlying faces for each surface. This is illustrated in Figure 4-9.
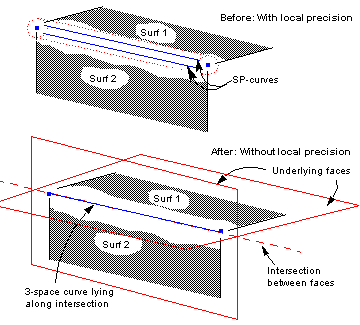
Figure 4-9 Removing local precision from an edge
This operation may not always be successful if the adjacent surfaces are tangent or nearly tangent.
|
|
When local precision is applied to a vertex, the precision value represents the radius of a sphere of uncertainty around the point of the vertex. The lower the precision, the larger the precision value, and the larger the sphere of uncertainty.
Vertex precision is usually set as a by-product of setting edge precision, either by calling PK_EDGE_set_precision or by other modeling operations. Your application should not normally need to set an individual precision for a vertex. However, if necessary, you can use PK_VERTEX_set_precision to set a vertex precision, provided that it is not:
PK_VERTEX_ask_precision returns the current precision of any vertex.
| <<< Model Structure | Chapters | Nominal Geometry >>> |