Adaptive Offset
Topics include:
- Non-G1 Discontinuities
- Local Area of High Curvature
- Geometric Singularities
- Illegal Parameterization
At the heart of many Local Operations commands is the need to offset a surface. In all cases LOPs first attempts an exact mathematical offset when offsetting any surface type. An exact surface offset O(u,v) is defined as
O(u,v) = S(u,v) + d * N(u,v)
where S(u,v) is the progenitor surface, d is the offset distance and N(u,v) is the normal to the progenitor surface. In the case of analytical surfaces, the correct analytical offset surface is obtained. For example, spheres offset to spheres.
Under certain conditions, correct offset surfaces cannot be obtained due to deficiencies in the progenitor surface. These deficiencies include local areas of high curvature, illegal parameterization, geometric singularities and non-g1 discontinuities. These problems can be present in the progenitor surface despite design intent.
In order to offset such surfaces, LOPS provides Adaptive Offsetting. This is a mechanism in which the surface is "corrected" before the offset (in order to obtain quality mathematical characteristics) so that the offset can be obtained.
Non-G1 Discontinuities
Non-G1 discontinuities cause self-intersections or gaps within the exact mathematical offset of the progenitor. To be able to offset non-G1 discontinuous surfaces, a local smoothing across the violating iso-param line is performed. The algorithm fails if the angle between the tangents is larger than a given angle tolerance or if the smoothing moves the surfaces locally by more than the greater of SPAresfit and 10% of the offset distance.
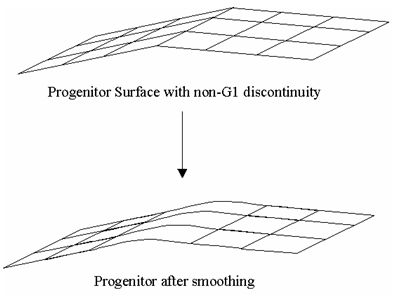
Figure. Progenitor Surface
Local Area of High Curvature
Local Areas of high curvature cause self intersections with the exact mathematical offset of the progenitor. In order to provide a well-behaved smooth offset surface, LOPS enacts a smoothing algorithm on the progenitor in order to obtain an offset surface. Smoothing is only performed if the smoothed version of the progenitor does not deviate by more than 5% of the offset distance to the original.
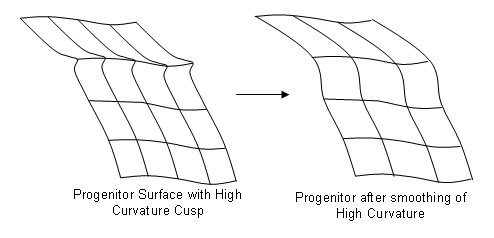
Figure. Smoothing of High Curvature Cusp
Geometric Singularities
A geometric singularity arises at a single point on a surface when the normal is said to be "multi-valued". That is, at one point on the surface, depending on the u,v parameter value given, a field of vectors can be obtained.
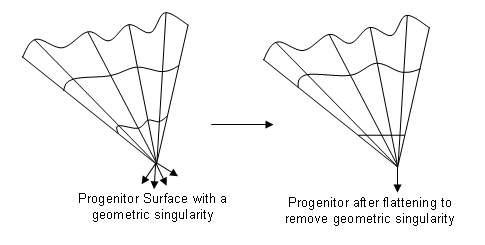
Figure. Flattening to Remove Singularity
LOPS flattens the area around the geometric singularity in order to provide proper normals.
Illegal Parameterization
An illegal parameterization in ACIS occurs when the du and dv vectors of a surface are parallel or anti-parallel. In order to obtain a proper offset surface, the progenitor surface is re-parameterized.
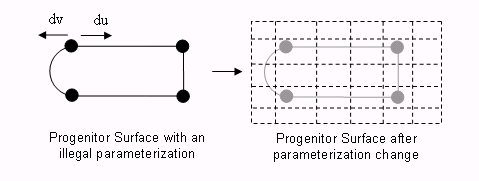
Figure. Progenitor Surface after Parameterization Change
Related topics:
Types of Local Operations
Topology
Body Repair
Blended Faces
Remove Faces
Defeaturing
Limitations
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.