Euler Operations

Contents

• 32.1 Introduction
  • 32.1.1 Terminology
    • 32.1.1.1 Edges
    • 32.1.1.2 Vertices
• 32.2 Functionality provided by Parasolid
  • 32.2.1 Summary of functionality
  • 32.2.2 Specific Euler operations
    • 32.2.2.1 PK_EDGE_euler_slit
    • 32.2.2.2 PK_FACE_euler_unslit
    • 32.2.2.3 PK_EDGE_euler_split
    • 32.2.2.4 PK_VERTEX_euler_merge_edges
    • 32.2.2.5 PK_LOOP_euler_make_edge
    • 32.2.2.6 PK_VERTEX_euler_delete
    • 32.2.2.7 PK_VERTEX_euler_split
    • 32.2.2.8 PK_EDGE_euler_merge_vertices
    • 32.2.2.9 PK_EDGE_euler_open_zip
    • 32.2.2.10 PK_EDGE_euler_close_zip
    • 32.2.2.11 PK_FACE_euler_make_loop
    • 32.2.2.12 PK_LOOP_euler_delete_isolated
    • 32.2.2.13 PK_LOOP_euler_delete_make_edge
    • 32.2.2.14 PK_EDGE_euler_delete_make_loop
    • 32.2.2.15 PK_LOOP_euler_make_edge_face
    • 32.2.2.16 PK_EDGE_euler_delete_with_face
    • 32.2.2.17 PK_LOOP_euler_make_edge_loop
    • 32.2.2.18 PK_EDGE_euler_delete_with_loop
    • 32.2.2.19 PK_FACE_euler_make_ring_face
    • 32.2.2.20 PK_EDGE_euler_delete_ring_face
    • 32.2.2.21 PK_FACE_euler_make_ring_loop
    • 32.2.2.22 PK_EDGE_euler_delete_ring_loop
    • 32.2.2.23 PK_LOOP_euler_transfer
    • 32.2.2.24 PK_FIN_euler_glue

[back to top]

32.1 Introduction

Euler operations are low-level functions that modify a small area of topology. Used in conjunction with functions to attach and detach geometry, these functions allow you to implement your own modeling operations, such as local operations and feature creation.

Euler operations always return a body with valid topological data-structures. However, the functions do not alter geometry - new topology created by an operation has no geometry attached, and any topology deleted by an operation has its geometry deleted first. This means that the resulting body is normally invalid, and you must attach suitable geometry to make the model valid yourself.

The fact that Euler operations are likely to produce invalid bodies makes these functions significantly different to most other PK functions. With the exception of functions to attach and detach geometry, other PK functions always return a valid body provided that it is valid when it is passed to the function.

The Euler operations are differentiated from other PK functions by including the word ‘euler’ in the function name, e.g. PK_EDGE_euler_split.

32.1.1 Terminology

The following terms are used in the Euler functionality in Parasolid.

32.1.1.1 Edges

Edges are classified as follows:

32.1.1.2 Vertices

The number of oriented edges at a vertex is as described in PK_VERTEX_ask_oriented_edges. A vertex with no oriented edges is called isolated.

A vertex is manifold if either:

• it is connected to one loop, which is isolated, or
• it is not connected to any isolated loops, all its edges are manifold, and its edges form a single face-connected set (i.e. the b-rep is locally manifold at the vertex).

[back to top]

32.2 Functionality provided by Parasolid

This section explains the functionality provided by the Euler operations in Parasolid.

• Section 32.2.1 provides a summary of the Euler operations available, for easy reference.
• Section 32.2.2 illustrates each Euler operation in turn.

32.2.1 Summary of functionality

The following table summarizes the Euler functionality that Parasolid offers:

32.2.2 Specific Euler operations

Each Euler operation is illustrated in this section. For more information, refer to the reference documentation for a specific function.

32.2.2.1 PK_EDGE_euler_slit

This function slits an edge lengthwise, creating a new slit face. The on_left argument specifies whether the new face lies on the left or right side of the given edge.

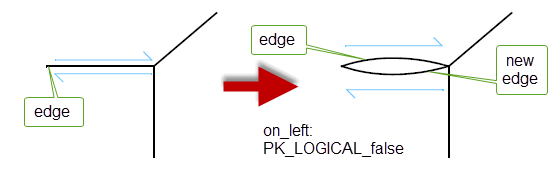
Figure 32-1 Slitting an edge lengthwise

32.2.2.2 PK_FACE_euler_unslit

This function deletes a slit face. The given face must have either one loop and two edges or two loops each with one ring edge.

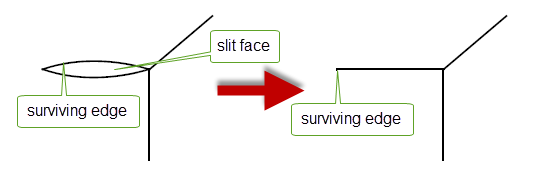
Figure 32-2 Deleting a slit face

32.2.2.3 PK_EDGE_euler_split

This function splits an edge by adding a vertex. The forward argument determines whether the new vertex is the forward or backward vertex of the edge.

Figure 32-3 Splitting an edge

32.2.2.4 PK_VERTEX_euler_merge_edges

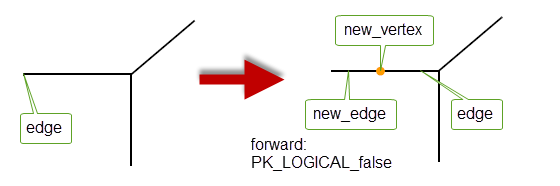
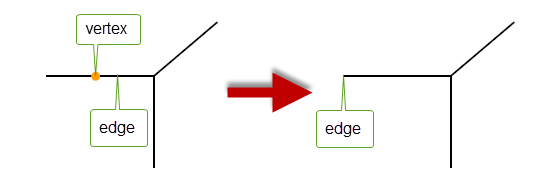
This function deletes a vertex from an edge.

Figure 32-4 Merging two edges

32.2.2.5 PK_LOOP_euler_make_edge

This function adds a trailing edge and vertex to a vertex in the specified loop . The vertex used is the forward vertex of the supplied fin . The direction of new_edge is towards new_vertex .

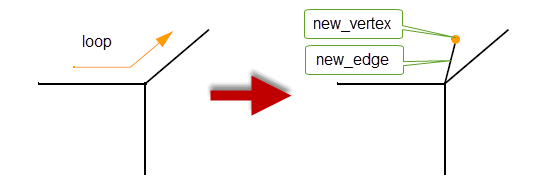
Figure 32-5 Adding a trailing edge to a fin

32.2.2.6 PK_VERTEX_euler_delete

This function deletes a vertex and its single attached edge.

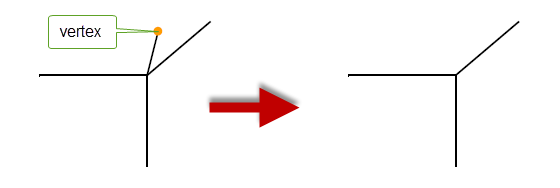
Figure 32-6 Deleting a vertex and its edge

32.2.2.7 PK_VERTEX_euler_split

This function splits a vertex, adding an intervening edge. The vertex must be a common forward vertex of the two fins supplied to the function.

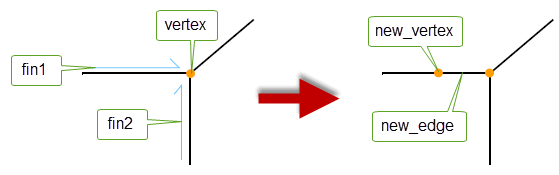
Figure 32-7 Replacing a vertex with an edge

32.2.2.8 PK_EDGE_euler_merge_vertices

This function merges two vertices, deleting the intervening edge.

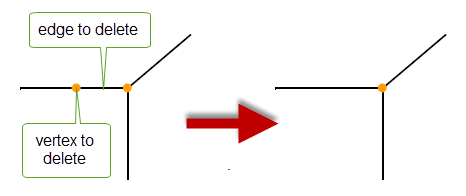
Figure 32-8 Replacing an edge with a vertex

32.2.2.9 PK_EDGE_euler_open_zip

This function splits an edge lengthwise, replacing it with two edges joined at one end. The vertex at which to split the edge is identified as the forward vertex of the supplied fin.

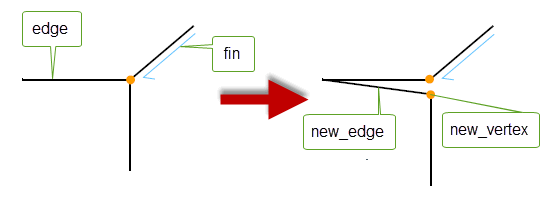
Figure 32-9 Splitting an edge into two lengthwise

32.2.2.10 PK_EDGE_euler_close_zip

This function ‘zips’ two edges together by merging the vertices at one end, deleting edge2 . There must be more than one edge at each of the vertices to be merged.

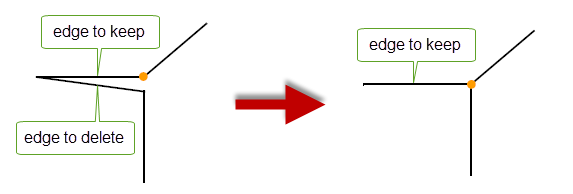
Figure 32-10 Merging two edges lengthwise

32.2.2.11 PK_FACE_euler_make_loop

This function adds an isolated vertex and loop to a face.

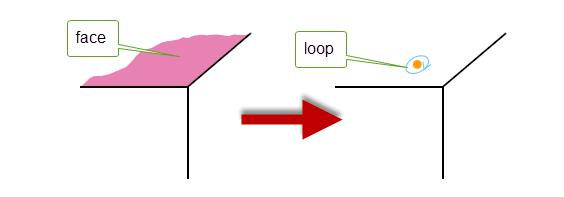
Figure 32-11 Adding a loop and isolated vertex to a face

32.2.2.12 PK_LOOP_euler_delete_isolated

This function deletes an isolated vertex and loop from a face.

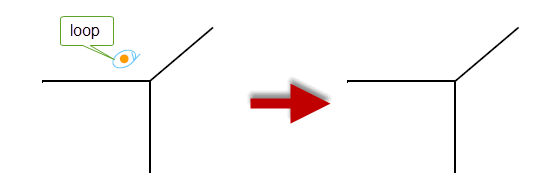
Figure 32-12 Deleting a loop and isolated vertex from a face

32.2.2.13 PK_LOOP_euler_delete_make_edge

This function merges two loops in the same face into one by joining their vertices with an edge. Loop2 is deleted.

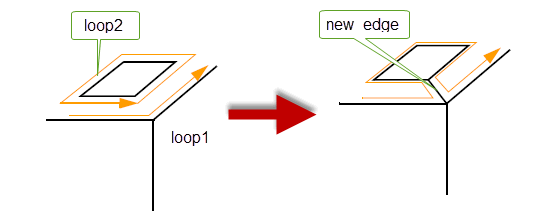
Figure 32-13 Adding a connecting edge to merge two loops

32.2.2.14 PK_EDGE_euler_delete_make_loop

This function deletes an edge from a loop splitting it into two loops. The logical forward determines which loop is the new one.

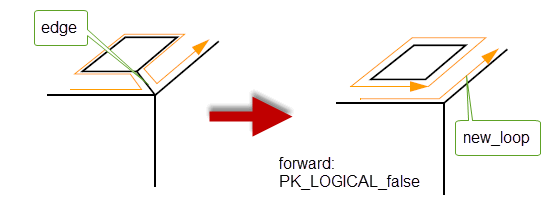
Figure 32-14 Deleting an edge to create two loops in a face

32.2.2.15 PK_LOOP_euler_make_edge_face

This function joins two vertices in the same loop, creating a new face. The new face is on the right of the new edge. The vertices are identified as the forward vertices of the supplied fins.

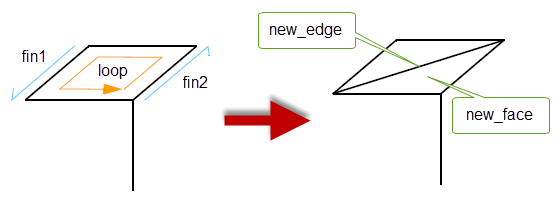
Figure 32-15 Joining two vertices in a loop

32.2.2.16 PK_EDGE_euler_delete_with_face

This function deletes an edge and merges two faces and loops into one. The on_left argument determines which face survives.

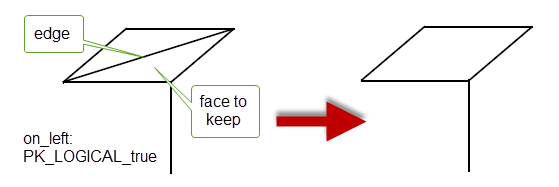
Figure 32-16 Merging two faces and loops

32.2.2.17 PK_LOOP_euler_make_edge_loop

This function is similar to PK_LOOP_euler_make_edge_face, but instead of splitting the face in two, it creates a new loop in the face, increasing its genus.

32.2.2.18 PK_EDGE_euler_delete_with_loop

This function is similar to PK_EDGE_euler_delete_with_face, except that it deletes an edge which has different loops in the same face on each side of it. It merges the loops into one, decreasing the genus of the face.

32.2.2.19 PK_FACE_euler_make_ring_face

This function splits a face by adding a new ring edge. The new face is always on the right of the edge.

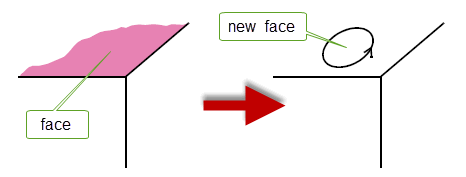
Figure 32-17 Splitting a face by adding a ring edge

32.2.2.20 PK_EDGE_euler_delete_ring_face

This function deletes a ring edge and a face.

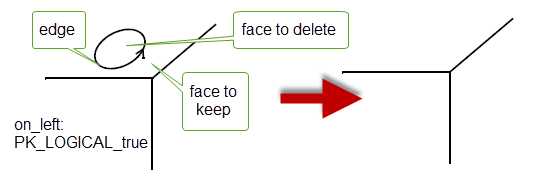
Figure 32-18 Deleting a ring edge and face

32.2.2.21 PK_FACE_euler_make_ring_loop

This function is similar to PK_FACE_euler_make_ring_face, except that instead of splitting the face in two, it creates a new loop in the face, thus increasing its genus.

32.2.2.22 PK_EDGE_euler_delete_ring_loop

This function is similar to PK_EDGE_euler_delete_with_face, except that it deletes a ring edge which has different loops from the same face on each side, thus decreasing the genus of the face.

32.2.2.23 PK_LOOP_euler_transfer

This function transfers a loop from one face to another. The two faces must have the same front and back shells.

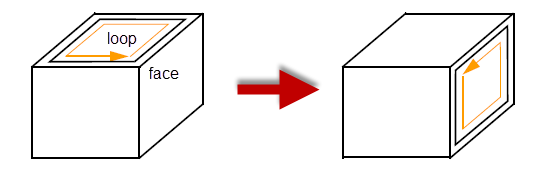
Figure 32-19 Transferring a loop to a different face

32.2.2.24 PK_FIN_euler_glue

This function glues two edges together by gluing fins together from two edges in the order in which they are passed to the function. The edge of the first fin passed to the function survives; the other edge is deleted.

[back to top]