Modeling Support

<<< Enquiry and Output Functions

Chapters

Simplifying Models >>>

Contents

• 39.1 Introduction
• 39.2 Standard representations
  • 39.2.1 Trimmed surfaces
  • 39.2.2 Concept of SP-curves
  • 39.2.3 Form of the SP-curve
• 39.3 Intersections
• 39.4 Transformations
  • 39.4.1 Creating transformations
  • 39.4.2 Applying transformations
• 39.5 Closest approach
  • 39.5.1 Supported entities
  • 39.5.2 Solution parametrization
  • 39.5.3 Functionality
  • 39.5.4 Optional controls
  • 39.5.5 Finding the parameter of a point on a curve/surface
• 39.6 Mid-surface generation
  • 39.6.1 Creation
  • 39.6.2 Trimming
  • 39.6.3 Tracking information
• 39.7 Splitting topology
• 39.8 Creating outline curves
  • 39.8.1 Returning topological entities
  • 39.8.2 Differentiating between several outlines
  • 39.8.3 Specifying options

[back to top]

39.1 Introduction

This chapter describes the support that Parasolid provides for modeling operations outside of Parasolid itself. This support is particularly useful when exporting data for use in other application. The following topics are covered:

• Standard representations, which are ways of outputting geometric information in a standard way, for use in other applications. See Section 39.2.
• The principles behind trimmed surfaces (Section 39.2.1) and SP-curves (Section 39.2.2).
• Intersection functions. See Section 39.3.
• Transformation functions. See Section 39.4.
• Closest Approach functionality. See Section 39.5.
• The generation of mid-surfaces. See Section 39.6.
• Splitting topology. See Section 39.7.
• Creating outline curves. See Section 39.8.

See also Chapter 40, "Simplifying Models".

[back to top]

39.2 Standard representations

Standard Representations are ways of outputting geometric information in a standard way, for use in other applications. The information returned is intended only for output.

PK_FACE_output_surf_trimmed provides a means of outputting a trimmed surface representation of a face. This is the part of the surface which represents the bounded surface region of the face.

A trimmed surface represents a bounded region on a parametrized surface. It does this by representing the region's boundary curves in the parameter space of the surface. Hence such a representation of a face consists of representing its edge loops (excluding any wire or bi-wire edges) in the parameter space of the surface.

The curves used to trim the surface in parameter space are represented by a curve entity called an SP-curve (surface parameter (space) curve). SP-curves are defined with respect to the surface's parameterization. For the trimmed surface representation, the SP-curves are used to approximate the edges that bound the face.

There are various surface and SP-curve options in use with the outputting of a trimmed surface representation of a face, these options control the following:

Surface Related Options

The surface whose parameter space is to be used can either be the surface attached to the face, or a B-spline representation of that face.

When the surface to use is a B-spline approximation further options that can be set are:

SP-curve Options

These options are available for SP-curves which are to be constructed and they cover:

Output Related Options

These options relate to the quantity of data to be returned, they are:

[back to top]

39.2.1 Trimmed surfaces

A trimmed surface is essentially a subset of a complete surface. It is described by giving the whole surface along with a set of curves that describe the boundary of that part of the whole surface that it occupies, it is helpful to view these curves as curves along which the surface was trimmed in order to leave the area of interest.

The convention that Parasolid applies when deciding which side of the cut is the area that is to be retained is:

• When holding the surface with its normal upward and cutting from the start of the curve to its end, the area on the left of the cut is the area retained.

Because Parasolid is cutting in the surface the description of the trimming curves is best expressed in terms of where to go in the surface. For this reason the trimming curves are curves in the parameter space of the surface.

For example, consider the top of the following cube where the surface is an infinite plane, the outer boundary is a rectangle in parameter space and the hole is a circle in parameter space:

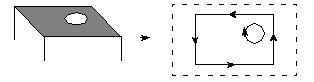
Figure 39-1 Trimming curves keeping the face on the left

As the trimming curves are in parameter space their shape need not correspond (directly) to that of the edges they represent. For example, consider the top of the following spun solid and its representation:

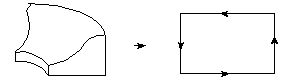
Figure 39-2 Representation of a spun solid

The shape of the SP-curves representing the boundaries of a face corresponds to how those boundaries would look if you painted constant parameter lines on the face, then took the face off, and stretched and ironed it flat so that all the constant parameter lines came out flat and evenly spaced.

For example:

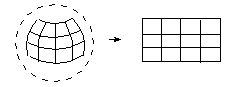
Figure 39-3 Flattening a face without a parametric singularity

There are occasions when ironing out and pasting flat with an even spacing result isn't possible without doing an infinite amount of stretching. This happens when the parametrization is bunched up to a point in one direction, at a parametric singularity. An example of this is at the N-pole of a sphere:

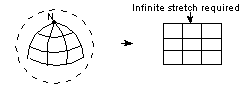
Figure 39-4 Flattening a face with a parametric singularity that requires an infinite stretch

In such cases, the trimming curves describing the boundaries may leave gaps as in:

Figure 39-5 Representation of a face with a parametric singularity that leaves a gap in the representation

Such descriptions with gaps in the boundaries are not always desirable. Options, PK_FACE_trim_confine_closed_c and PK_FACE_trim_confine_periph_c, when using PK_FACE_output_surf_trimmed are designed to make the trimming curves join up in the parameter space by adding extra trimming curves to fill in the 'infinite stretch' tear as illustrated in the following illustration:

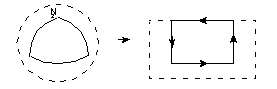
Figure 39-6 Closing the gap in the representation of a face with a parametric singularity

The same effect, as described in Figure 39-6 results when using the degeneracies option PK_FACE_trim_degen_yes_c. This option also represents the isolated parametric degeneracies.

Gaps can also appear in the boundary description in parameter space through the way periodicities are treated. Surfaces with periodicities can be viewed as flat surfaces glued along a seam line. The viewpoint requires the trimmed surface output to first cut the (sur)face along the seam and then proceed to iron it out flat. This process, however, cuts and opens out boundaries as well as the surface.

Figure 39-7 Cutting and opening boundaries as well as the surface (option PK_FACE_trim_confine_yes_c)

This view of periodic surfaces is optional when using the options PK_FACE_trim_confine_yes_c in PK_FACE_output_surf_trimmed. The alternative is to follow the boundaries as they cross the seam, in which case they are not confined to a single period of the parameter space, by using the option PK_FACE_trim_confine_no_c.

Figure 39-8 Following the boundaries as they cross the seamline (option PK_FACE_trim_confine_no_c)

When it is necessary to close the loops, use either of the options PK_FACE_trim_confine_closed_c or PK_FACE_trim_confine_periph_c in PK_FACE_output_surf_trimmed. Here the outputting a trimmed surface function essentially views the seam-line cuts as a face boundary that it had earlier been convenient to ignore. In the previous example the following view is taken.

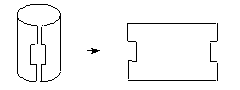
Figure 39-9 Using the option PK_FACE_trim_confine_closed_c or PK_FACE_trim_confine_periph_c to close the loops

Further to this theme of cutting surfaces along invisible seams, the following illustration shows that the result of cutting the face on the illustrated seam would result in two individual pieces:

Figure 39-10 Cutting a surface along an invisible seam, producing two trimmed surfaces

Here PK_FACE_output_surf_trimmed is forced to produce two trimmed surfaces when it is asked to cut the face and produce closed, joined up loops. In effect, our viewpoint implied that the original face was actually two faces glued together along the ignored seam.

The word 'trimmed' in trimmed surface implies that something has been removed from the whole surface. In considering faces there is one kind of boundary that effectively trims nothing. This is the natural boundary of the surface, i.e. that part of the surface that marks out the limits of its definition.

An example of such a boundary is the rectangle of bounding constant parameter lines, B-curves of a B-surface. Spheres, on the other hand, have no such boundary.

If this natural boundary coincides with one of the face boundaries then, as it effectively trims nothing, it can readily be accepted that it be omitted from the trimmed surface PK_FACE_trim_confine_closed_c is selected. Its omission is independent of whether the face has holes or not. For example:

Figure 39-11 Omitting the natural boundary when using the option PK_FACE_trim_confine_closed_c

Gaps in SP-curve Loops

To summarize, the following factors can lead to occurrences when the SP-curve loops are not closed:

• SP-curves are present only on the fins of tolerance edges;
• Tolerant edges have tolerant vertices;
• Faces with only accurate edges may have tolerant vertices;
• Tolerant vertices are there to hide gaps in edge/fin geometry.

Tolerances could be said to be present in Parasolid to reflect the extent to which geometries don't meet. For example, edge tolerances reflect the extent to which surfaces don't meet at a common boundary, and vertex tolerances reflect the size of gaps between edge geometries meeting.

When the gaps represent gaps between edge/fin geometries at a tolerant vertex, the size of the gaps should be less than twice the tolerance of the vertex.

Otherwise accurate faces may have tolerant vertices where the tolerant edge of a neighboring face intersects its boundary. While it may be expected that the accurate edges of the face meet there, this is not always possible. A simple example of this would be a cube with the top face replaced by two planar sheets, one of which is a micron above the other, and which share a common tolerant edge. All edges on the cube are accurate except for the mid-line across the top of the cube. Figure 39-12 shows the side view of the cube.

Figure 39-12 Two planar sheets sharing a common tolerant edge

The top two accurate edges do not intersect, and typically have a gap at the vertex of about one micron - these are the gaps that Parasolid is trying to hide from you, and deal with, through the use of tolerances.

[back to top]

39.2.2 Concept of SP-curves

A parametrizable surface is defined in terms of an evaluator function which given two parametric values, u and v, maps to a single point in space. Typically this function is only defined on a certain range of values in u and v.

f(u, v) -> (x, y, z) u e [a, b], v e [c, d]

We can consider this vector valued function as three scalar valued functions, with the same arguments.

f(u, v) -> (f1(u, v), f2(u, v), f3(u, v))

Consider a function which maps from a single parametric value t, to a pair of values, u and v.

g(t) -> (u, v) t e [l, m]

Similarly to the surface function, the function g, which maps to u,v space can be considered as two scalar functions.

g(t) -> (g1(t), g2(t))

By combining the two functions we can have a mapping from a single parameter value to a single point in space. Consider now, all the values of t in a particular range, or interval. Each value maps onto a point in space, and so we have created a parametric curve.

f(g(t)) -> (x, y, z) t e [l, m]

In the scalar format, for completeness.

f(g(t)) -> (f1(g1(t), g2(t)), f2(g1(t), g2(t)), f3(g1(t), g2(t)))

Because of the way that this curve has been constructed, we know that all the points of the curve lie on the surface. The 2-dimensional function g, which maps t into u,v space is called a Surface Parameter (space) curve, or SP-curve.

An SP-curve therefore represents a 3-space curve as a curve in the parameter space of the surface.

[back to top]

39.2.3 Form of the SP-curve

In Parasolid, SP-curves are 2d B-spline curves, which are allowed to be rational. The chapter on the mathematical forms has details on B-spline curves in 3d. 2d B-spline curves are very similar. It should be understood that whilst the B-spline vertices in other cases are points in 3d space, the 2d B-spline vertices of SP-curves represent points in the parameter space of the basis surface.

An SP-curve must be G1 continuous, and if periodic, it must meet itself with G1 continuity, surface degeneracies may only appear at the start or end of an SP-curve. An SP-curve may pass through a periodic parameter space boundary, but must lie within the parameter range defined by PK_SURF_ask_params on limited surfaces. On limited surfaces, it is permissible for the B-spline vertices to lie out of parameter range if the B-spline curve so defined lies within the range.

The SP-curve is parametrized according to the underlying knot vector.

The SP-curve entity exists for:

• the purpose of outputting trimmed surface representations, using PK_FACE_output_surf_trimmed;
• import of application trimmed surface data into Parasolid.

[back to top]

39.3 Intersections

The following intersection functionality is available:

All functions, except PK_FACE_intersect_curve, take an options structure which for performance purposes allows you to specify areas of interest in the body by stipulating:

box

A 3-space box of interest

• all intersections inside the specified box are returned, but ones outside of it may not be
• applies to all functions except PK_FACE_intersect_curve

uvbox_1 and uvbox_2

Parameter boxes for the two entities

• the intersection curves returned are not trimmed to lie within the boundaries of the parameter box(es)
• applies to PK_FACE_intersect_face and PK_FACE_intersect_surf

common_surf

The surface which contains both of the curves

• applies to PK_CURVE_intersect_curve

[back to top]

39.4 Transformations

The Parasolid PK interface supports homogenous coordinate transformations. These allow translation, scale (equal and non-uniform), rotation, shear and reflection transformations to be specified. These transformations can then be combined to give more general transformations.

Transformations can then be applied to individual geometrical entities or to whole bodies.

[back to top]

39.4.1 Creating transformations

Many of the basic transformations are available directly via:

• PK_TRANSF_create_equal_scale
• PK_TRANSF_create_reflection
• PK_TRANSF_create_rotation
• PK_TRANSF_create_translation

In addition to these functions, PK_TRANSF_create allows you to create any transformation directly. For example, a non-uniform scaling of 2 in X, 3 in Y and 4 in Z can be generated from the PK_TRANSF_create function with matrix:

( 2 0 0 0 )
( 0 3 0 0 )
( 0 0 4 0 )
( 0 0 0 1 )

as input. The documentation of the standard form, PK_TRANSF_sf_t, explains the mathematics underlying this matrix. Parasolid currently does not allow perspective terms in transformations used in modeling operations. This means that the first 3 elements of the 4th column of the matrix must be zero.

Transformations can be combined by PK_TRANSF_transform.

[back to top]

39.4.2 Applying transformations

Transformations can be applied to points, curves, surfaces and sheet or solid bodies.

Transforming geometry

PK_GEOM_transform takes as input a point, curve or surface, a transformation and a tolerance. It generates a new point, curve or surface being the transformation of the supplied geometry. This means that, for example, surface of faces in a body can be supplied as input without affecting the integrity of the body.

The tolerance argument comes into play if Parasolid cannot exactly transform the geometry and gives the deviation of the resultant geometry from the mathematical ideal. Sometimes no exact transformation can be achieved in the geometry class that is changed.

For example, in surfaces:

• planes can always be transformed to planes
• spheres can always be exactly transformed but may result in B-surfaces
• B-surfaces can always be exactly transformed
• offset surfaces usually transform to approximate B-surfaces

Transforming bodies

PK_BODY_transform_2 takes a sheet or solid body, a transformation and a tolerance for geometry which may have to be approximated.

The body is transformed. Face surfaces and edge curves may have to be approximated in order to achieve the desired result. Intersection curves are recalculated between transformed face surfaces unless the intersection and face surfaces can be transformed exactly.

It can happen that edges and vertices become tolerant as a result of this operation. For example, a smooth edge between faces often transforms to a tolerant smooth edge. Some topology changes, such as the elimination of edges made too short by transformation, are supported.

[back to top]

39.5 Closest approach

The closest approach functionality returns the global minimum distance, or all distances that are the local minima of distance, between:

• a position vector and an entity, returning:
• the global minimum distance between the position vector and the entity; or a list of the local minimum distances between them
• solution points on the entity at which the minimum distances are achieved
• two entities, returning:
• the global minimum distance between the two entities; or a list of the local minimum distances between them
• pairs of solution points, one on each entity, between which the minimum distances are achieved

[back to top]

39.5.1 Supported entities

The following entity types are supported:

• Geometrical - point; curve; surface.
• Topological - vertex; edge; face; body.

If an entity is topological and a solution is found to lie on a sub-topology, then this sub-topology is identified, e.g. an edge or vertex of a face, or a face of a body.

For entity - entity enquiries only the following are allowed:

• geometrical - geometrical
• topological - topological

Topological - geometrical enquiries are not allowed.

[back to top]

39.5.2 Solution parametrization

When a solution is linked to a surface or a curve, the corresponding surface or curve parameters is determined. Preference is given to returning the surface parameters. The parameters returned depend upon the entity and sub-topology on which the solution lies, see the following table.

The following figure and table illustrates what sub-topology is identified and what parametrization is used when the distance is enquired between a point and a body, face, or edge. The table contains the expected outcome for enquiries between the points and the topology of the solid cube.

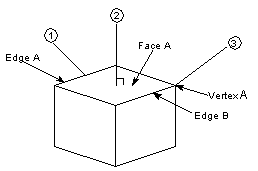
Figure 39-13 Identifying sub-topology

All the closest approach solutions in the table are unique, because for each enquiry there is only 1 solution point on the entity. If the distance was enquired from a point in the center of the cube to the cube, the solution would not be unique as all the faces would be the same distance from the point. For such a case only one solution is returned if only the global minimum is requested, and no indication of the existence of the other solutions is made. Where all local minima are required, all 6 minima, one in the center of each face are returned.

[back to top]

39.5.3 Functionality

[back to top]

39.5.4 Optional controls

All the above functions take an options structure containing some or all of the following options which allow you to specify additional information:

Supplying an estimate

Figure 39-14 Estimates

Restriction

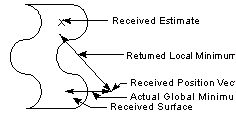
Estimates are not allowed for computations involving bodies, e.g. a face cannot be given an estimate for a face - body computation.

[back to top]

39.5.5 Finding the parameter of a point on a curve/surface

PK_CURVE_parametrise_vector finds the parameter of a point on a curve and PK_SURF_parameterise_vector finds it on a surface.

[back to top]

39.6 Mid-surface generation

Within Parasolid Mid-Surface Generation is the creation and trimming of neutral sheets.

Neutral sheets are intended for use when performing finite element analysis of thin-walled parts by representing a solid model containing thin sections as a collection of sheet bodies which can then be discretized and analyzed.

The process of creating neutral sheets may be thought of as the opposite of creating a solid body by thickening a collection of sheets. A neutral sheet may have any number of faces but these must all share the same surface.

This functionality is in two stages:

• the creation of neutral sheets (sheet bodies), either by using PK_FACE_make_neutral_sheet or by the application creating its own sheet bodies; and
• the trimming of the resulting sheet bodies, using PK_BODY_trim_neutral_sheets, to ensure that the neutral sheets are the correct size and shape and that there are edges on each sheet where two (or more) sheets meet.

[back to top]

39.6.1 Creation

PK_FACE_make_neutral_sheet takes 2 faces, which may be from any body, and a position parameter. The surfaces of the faces are used to create another surface (the neutral surface) which is between them and whose position depends on the value of the position parameter. For example, if the position parameter is 0, then the resulting surface is halfway between the surfaces on the given faces. The neutral surface is then attached to a single faced sheet which is then returned.

Face set pairs

The required neutral sheet idealization of the solid body is specified as a series of face set pairs - one pair for each sheet. Each face set contains the faces on the solid on one side of the neutral sheet, the pair of sets therefore contains a set for each side of the sheet. The relationships between neutral sheets are derived from the face set pairs.

For a face set to be valid it must comply with the following condition:

• Let 'p' be a point in the interior of a face, and let the corresponding point 'p1' on the neutral surface be the one found by projecting 'p' along the normal to the neutral surface. The alignment of 'p' is now defined to be the sign of the dot product of the face normal at 'p' with the normal to the neutral sheet at 'p1'. All the points in the interior of a face should have the same non-zero alignment, this is termed the alignment of the face. Points on the edges of a face may have a zero alignment.

All the faces in the first set of a pair must have a positive alignment and the faces in the second set must have a negative alignment.

For example, in the following illustration (a section of a swept body):

• the pair for the shown neutral surface would be ({f1, f2, f4}, {f6});
• the pair cannot contain f5 since there are points in this face with different alignments;
• it should not contain f3 since its alignment is 0;
• similarly, the pair cannot be ({ f1, f6}), ( {f2, f4}) since f1 and f6 do not have the same alignment; and
• the direction of the face normal on the neutral sheet is the same as that on the faces f1, f2 and f4.

Figure 39-15 A simple face set

A slightly more complicated example is shown in Figure 39-16 - suppose that the pairs are ({f1}, {f2}), ({f4}, {f6}) and ({f3, f7}, {f8}). It now does not make sense for face f5 to belong to this last pair due to the pairing of f4 and f6. The resulting neutral sheets are shown by the dashed lines.

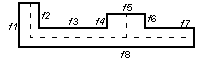
Figure 39-16 A body with three face set pairs

Classification of faces

Once the pairs have been specified for a body, each face in the solid body may be classified as one of:

• a pair face (one which is a member of a face set);
• a side face (one which is adjacent to faces from different sets in a face set pair);
• neither (a) nor (b).

This restricts to a certain extent the type of body which may be used. For example, a face cannot be both a pair face and a side face and neither may a single face belong to more that one pair.

In Figure 39-15 f5 is a side face, but f3 is not a side face since it does not connect faces in the pair with opposing alignments, therefore f3 is regarded as unclassified.

[back to top]

39.6.2 Trimming

Trimming is done by using the information encoded in the face set pairs to scribe edges onto the neutral sheets. These edges define either the limits of the neutral sheet or where two neutral sheets meet each other. Once all the edges have been created, any unwanted faces on the sheet are deleted.

There are 3 reasons for an edge to be created on the neutral sheet:

• two (or more) neutral sheets meet, an edge is created on each sheet along the common curve of intersection;
• at the exterior boundary of the neutral sheet this is either where the neutral sheet intersects the surface of a side face or where it meets another neutral sheet; and
• the target body changes thickness abruptly. This occurs where there is an unclassified face. The edge next to the unclassified face is projected along the normal to the neutral surface onto the neutral sheet.

A simple case is shown in Figure 39-17 (a) shows a simple swept profile. There are 3 face set pairs in this example, the corresponding untrimmed neutral sheets are shown in (b), and the neutral sheets after trimming are shown in (c).

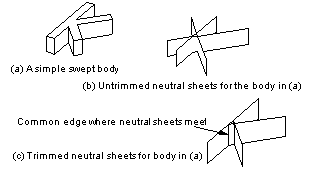
Figure 39-17 A simple swept body

In Figure 39-18 (a) shows another swept body, this time with a boss added. There are two face set pairs in this example, one for the horizontal plate with the boss and one for the upright. The resulting trimmed neutral sheets are shown in (b). Notice that the edge around the boss has been projected onto the corresponding neutral sheet.

Figure 39-18 Swept body with a boss added

A final example is shown in Figure 39-19 in which there are two face set pairs, one for the base plate and one for the tab. Notice that the neutral sheet of the base plate has an edge in the middle where two sheets meet.

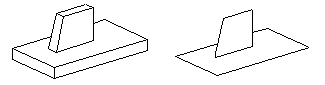
Figure 39-19 Neutral sheets for a solid plate with a tab (RH illustration)

[back to top]

39.6.3 Tracking information

Each face on a neutral sheet has usually arisen from the projection of two faces on the target body (one on each side). For example, in Figure 39-18 the top side of the circular face is the projection of the whole of the circular face on the top of the boss, the underside is part of the projection of the rectangular face on the underside of the target body. Similarly, the surrounding face is part of the projection of the rectangular face around the boss and the face on the underside.

Currently, the trimming function gathers and returns this information. For each side of every face on each neutral sheet it returns a list of faces on the target which project onto this face on the neutral sheet. There is usually one target face for each side. However, sometimes there may be 2 on one side, or there may be none.

[back to top]

39.7 Splitting topology

The following functions are used to split topological entities:

You can use these functions to create additional edges or faces in a model. For example, Parasolid does not split topology at periodic boundaries by default - a cylindrical face is not given a "seam". You can call PK_FACE_split_at_param to create a seam, as shown in Figure 39-20.

Figure 39-20 Splitting a periodic face in order to produce a seam

PK_EDGE_split_at_param receives and returns the following arguments:

PK_EDGE_split_at_param accepts both tolerant and accurate edges. In order for the edge to be split successfully, the following must all be true:

• param must be inside the range of edge
• param must not evaluate to a point coincident with any vertex on edge
• edge must have attached geometry

PK_FACE_split_at_param receives and returns the following arguments:

If the face is split successfully, then new edges are created. This in turn may lead to the creation of new faces. If new faces are created, the original face lies on the right of one of the new edges. All new edges go in the direction of param_dir .

[back to top]

39.8 Creating outline curves

PK_BODY_make_curves_outline is used to create outlines from one or more solid or sheet bodies. An outline consists of an ordered set of connected curves, as shown in Figure 39-21. These can either be projected onto a specified plane, or remain as 3-dimensional curves to retain their 3D information.

Figure 39-21 Creating outline curves for a body

The outlines created must consist of one or more closed loops, each with a non-empty interior. For example, you cannot create an outline of a sheet body if any part of it is edge-on in the specified view direction.

PK_BODY_make_curves_outline receives and returns the following arguments:

The returned curves , intervals , topols , outlines , and curve_tolerances are all of length n_curves .

Any new curves that are created as a result of the function call are attached as construction geometry to the original bodies.

[back to top]

39.8.1 Returning topological entities

As well as the outline curves themselves, PK_BODY_make_curves_outline can also return, in topols , the topological entities from the original bodies that were used to create each curve. The entity that is returned for each curve depends on how the curve was derived:

• If a curve in the outline was derived from an edge in the original body, that edge is returned.
• If a curve in the outline was derived from a silhouette curve in the original body, the face on which the silhouette lies is returned.

This is illustrated in Figure 39-22, which shows an outline consisting of 4 curves.

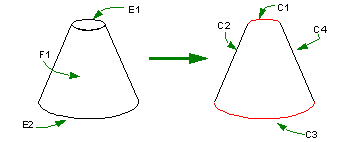
Figure 39-22 Topological entities used to create outline curves

The topological entities that are returned for each curve in the outline are shown below. Note that the face F1 is returned for both C2 and C4, since these curves are created from the silhouette of F1.

[back to top]

39.8.2 Differentiating between several outlines

The curves returned by PK_BODY_make_curves_outline often often make up more than one outline, as shown in Figure 39-23. This may happen when you create outlines of several overlapping bodies, as shown in the figure, or when you create outlines of a body containing holes. When several outlines are returned, use the value of outlines to find which curves make up each outline.

Figure 39-23 Returning several outlines from PK_BODY_make_curves_outline

Suppose, for example, that three outlines were returned, consisting of 2, 7, and 2 curves respectively (as in Figure 39-23). In this case, the value of outlines would be

(0 0 1 1 1 1 1 1 1 2 2 )

This indicates that the first 4 curves returned form one outline, the next 5 form another outline, and the last 6 form a third outline.

[back to top]

39.8.3 Specifying options

You can set a number of options when creating outline curves, using the associated PK_BODY_make_curves_outline_o_t options structure. The options you can set are as follows:

[back to top]