 |
Enquiry and Output Functions |
| <<< Wire Modeling | Chapters | Modeling Support >>> |
The object of this chapter is to list and where necessary explain briefly what each enquiry and output function does so that you can decide which are most appropriate in a particular situation.
For a full description of each function, refer to the relevant Parasolid Programming Reference Manual.
| Function | Description |
|---|---|
|
Is the given fin travelling in the same direction as its owning edge? |
|
Geometric Output Functions produce information on Geometric Entities. The data which is returned is often little more than outputting the information which is stored with the entity. Other relevant sections include "General enquiries", in this chapter and "Standard representations" in Chapter 39, "Modeling Support".
Information about Mass and related properties.
| Function | Description |
|---|---|
This function calculates the following geometric properties of relevant topological entities or list of entities:
If a list is given, all the entities must be of the same type. However, bodies can have a different mass density.
When a list of faces or sheet bodies is given, the function treats them as a single solid entity, but the mass is not returned. No checking is done on whether the faces or sheet bodies form a solid boundary, if they do not, the returned results are likely to be meaningless.
An accuracy parameter is provided which can be used to speed up the operation when maximum accuracy is not essential.
A token can also be provided to instruct Parasolid to estimate the degree of inaccuracy of the values returned.
This function contains an option for an alternative method of calculating mass properties of dimension 2 and 3. These are calculated by generating a facet mesh for each face referenced and then combining the contributions for each facet, this provides verification of the main parameter algorithm. A chordal tolerance, the equivalent to the
curve_chord_tol
and
surface_plane_tol
as used by PK_TOPOL_facet can be applied.
The functions in this section are concerned with the connections between entities within the data structure. Some give information on what those connections are. For information about functions which return information about individual entities, see the sections on "Topological enquiries", "Geometric output", and "General enquiries", also in this chapter.
| Function | Description |
|---|---|
|
Functions that return connectivity data between the given entity and its associated body. For each of these functions, the data is not returned in any predictable order with the exception of PK_BODY_ask_faces, which returns the faces in a standard order, only for solids that were created using the primitive creation functions. |
|
|
Laminar edges are those edges which bound a single face, i.e. they have exactly one fin. |
|
|
Functions that return connectivity data between the given entity and its associated curve. |
|
|
Functions that return connectivity data between the given entity and its associated edge. |
|
|
Returns the set of groups of which the given entity is a member |
|
|
Functions that return connectivity data between the given entity and its associated face. |
|
|
Functions that return connectivity data between the given entity and its associated fin. |
|
|
Functions that return connectivity data between the given entity and its associated loop. |
|
|
Returns the set of geometric entities in the part which are not attached to the parts topology |
|
|
Removes geometric entities from a parts construction geometry |
|
|
Functions that return connectivity data between the given entity and its associated partition. |
|
|
Functions that return connectivity data between the given entity and its associated shell. |
|
|
Functions that return connectivity data between the given entity and its associated vertex. |
|
For solids which were created using the primitive creation functions:
the ordering of these faces is always the same. For these solids it is as follows:
These only have a single face.
The ordering of the faces in cones depends on whether either of the radii is zero. If the lower radius is non-zero, the planar face containing the point supplied (to PK_BODY_create_solid_cone) is the base face. If the upper radius is non-zero, the other planar face is the top face.
The faces are ordered as follows:
The ordering of the block faces is related to the base face, and the first side face. The side faces are counted anticlockwise around the axis direction and are named first, second, third and fourth side faces,
When the axis is along the Z axis the first side face is the face in the -Y direction. At other orientations, one of the side faces is chosen to be first.
If the axis is along the Z axis, the ordering becomes:
Where -Y indicates the face which is parallel to X-Z plane, and extreme in the -Y direction.
The ordering of the prism faces is related to the base face, and the first side face. The side faces counting anticlockwise along the axis direction are named the first side face, second side face, etc.
The ordering for an n-sided prism is as follows:
Parasolid offers facilities to perform parameter space enquiries on general curves and surfaces. This section describes the parametrisation for surfaces and curves, and lists those functions which use the parametric information.
Curves have a representation of the form R(t), where R is a vector valued function of a parameter t. Surfaces have a representation of the form R(u, v), where R is a vector valued function of parameters u and v. All curves and surfaces which can exist in a model are representable in this form, with the exception of SP-curves. The parameters t, u, and v may take a range of values, which varies according to the type of curve or surface.
The parameter ranges, and other properties of the parametrisation, can be found from two PK functions, PK_CURVE_ask_interval and PK_SURF_ask_uvbox. The vector valued functions R(t), R(u, v) can be considered as mappings from the parameter space, to three-space. PK_CURVE_eval (PK_CURVE_eval_with_tangent) and PK_SURF_eval (PK_SURF_eval_with_normal) perform these mappings and the inverse mappings are performed by PK_CURVE_parameterise_vector and PK_SURF_parameterise_vector.
The parametrisation of a curve or surface is invariant under translation and rotation, but not under reflection or a scaling transformation. For instance a curve is represented by F(t) is transformed by T. The parametrisation of the resulting curve is G(t). If the transformation T is a translation or rotation then
In this chapter, the following conventions apply:
| Function | Description |
|---|---|
|
Returns interval indicating the parametric bounds of the given curve |
|
A straight line has a parametric representation of the form:
The range for t is (-infinity, +infinity).

Figure 38-1 Curve parametrisation - straight line
The reference point P and direction D can be obtained from PK_LINE_ask. The parameter t represents the signed distance of the point R(t) on the line from the reference point P.
A circle has a parametric representation of the form:
where C is the center of the circle, r is the circle radius, X and Y are axes in the circle plane.

Figure 38-2 Curve parametrisation - circle
The range for t is [0, 2pi). The parametrisation is periodic, so that PK_CURVE_eval can take any value of t and returns a point on the circle.
The circle center C, the axis A, the ref_direction X, and radius r can be obtained from PK_CIRCLE_ask.
The Y axis is given by the vector cross product of A and X.
Alternatively, the Y axis can be obtained by evaluating R(pi/2) using PK_CURVE_eval, and applying the formula
The parameter t represents the angle around the circle, measured in radians from the X axis. It runs clockwise when viewed along the axis A.
An ellipse has a parametric representation of the form:
C is the center of the ellipse, a is the major radius, X is the major axis, b is the minor radius, Y is the minor axis.

Figure 38-3 Curve parametrisation - ellipse
The range for t is [0, 2pi); the parametrisation is periodic, so PK_CURVE_eval works for any value of t, but PK_CURVE_parameterise_vector always returns a value in the above range.
The ellipse center C, the axis A, the ref_direction X and the radii a and b can be obtained from PK_ELLIPSE_ask. The ellipse parametrisation is equivalent to the parametrisation of a circle with radius a, and the same center as the ellipse. The point R(t) on the ellipse can be projected onto the circle by projecting it parallel to the Y axis and away from the X axis. The parameter t represents the angle around the circle, measured from the X axis, made by the projection of R(t). The following diagram illustrates this.

Figure 38-4 Curve parametrisation - curve compared with an ellipse
B-curves (including B-splines which are represented internally as Bezier) have their own parametrisation.
For details, see Chapter 26, "The Mathematical Form of B-Geometry".
An intersection curve does not have an explicit parametric form. A parametrisation is supported for it, however, which is based on a polyline approximation of the curve.
The parametrisation has the following properties:
| Function | Description |
|---|---|
A plane has a parametric representation of the form:

Figure 38-5 Surface parametrisation - plane
where P is a point on the plane. X and Y are axes in the plane.
The range for u is (-infinity, +infinity). The range for v is (-infinity, +infinity).
The reference point P, reference direction X and plane normal N can be obtained from PK_PLANE_ask.
The Y axis is the vector product of the plane normal N and the X axis: Y = N X X
Alternatively, the Y axis can be obtained by evaluating R(0, 1) using PK_SURF_eval, and applying the formula
The parameters u and v both represent distances: the distance of the point R(u, v) from the reference point P projected onto the X and Y axes respectively.
A cylinder has a parametric representation of the form:

Figure 38-6 Surface parametrisation - cylinder
The range for u is [0, 2pi); the parametrisation is periodic, so PK_SURF_eval works for any value of u, but PK_SURF_parameterise_vector always returns a value in the above range. The range for v is (-infinity, +infinity).
The reference point P, cylinder axis A, reference direction X and radius r can be obtained from PK_CYL_ask.
The Y axis is the vector cross product of the cylinder axis A and the X axis: Y = A X X.
Alternatively, the Y axis can be obtained by evaluating R(pi/2, 0) using PK_SURF_eval, and applying the formula
The parameter u represents the angle around the cylinder, measured in radians, from the X axis. It runs clockwise when viewed along the A axis. The parameter v represents the distance from R(u, v) to the reference point P, projected onto the axis.
A cone in Parasolid is only half of a mathematical cone. By convention, the cone axis points in the direction of increasing radius. A cone has a parametric representation of the form:
P is a point on the cone axis, r is the cone radius at the point P. A is the cone axis (unit vector). X and Y are unit vectors such that A, X and Y form an orthonormal set, i.e. Y = A x X. 'a' is the cone half angle.

Figure 38-7 Surface parametrisation - cone
The range for u is [0,2pi); the parametrisation is periodic, so PK_SURF_eval works for any value of u, but PK_SURF_parameterise_vector always returns a value in the above range.
The range for v is [-r cot(a), +infinity).
The reference point P, cone axis A, reference direction X and radius r at P and half angle a can be obtained from PK_CONE_ask.
The Y axis is the vector product of the X axis and the cone axis A: Y = X X A.
Alternatively, the Y axis can be obtained by evaluating R(pi/2,1) using PK_SURF_eval, and applying the formula
The parameter u represents the angle around the cone, measured from the X axis. It runs clockwise when viewed along the A axis. The parameter v represents the distance from R(u, v) to the reference point P, projected onto the axis. It runs away from the cone apex.
A torus has a parametric representation of the form:

Figure 38-8 Surface parametrisation - torus
C is center of the torus. A is the torus axis (unit vector), a is the major radius, b is the minor radius.
X and Y are unit vectors such that A, X and Y form an orthonormal set.
In Parasolid, there are three types of torus:
The limiting case a=b is allowed; it is called an 'osculating apple', but there is no 'lemon' surface corresponding to this case.
The limiting case a=0 cannot be represented as a torus; this is a sphere.
The range for u is [0, 2pi); the parametrisation is periodic, so PK_SURF_eval works for any value of u, but PK_SURF_parameterise_vector always returns a value in the above range.
The range for v varies according to the type of torus:
| Torus type | V range |
|---|---|
|
The range is [-pi, pi); the parametrisation is periodic, so PK_SURF_eval works for any value of v, but PK_SURF_parameterise_vector always return a value in the above range. |
|
The v parametrisation for the doughnut is periodic, for the lemon and apple it is not.
The torus center C, axis A, reference direction X, major radius a and minor radius b can be obtained from PK_TORUS_ask.
The Y axis is the vector product of the torus axis A and the X axis: Y = A X X. Alternatively, the Y axis can be obtained by evaluating R(p/2, 0) using PK_SURF_eval, and applying the formula
The parameter u represents the angle around the A axis, measured from the X axis. It runs clockwise when viewed along the A axis. The parameter v represents the angle around the torus spine, measured from the circle with center C, axis A and radius a + b. It runs clockwise when viewed along the spine.
A sphere has a parametric representation of the form:
C is center of the sphere, r is the sphere radius. A, X and Y form an orthonormal axis set.
The range for u is [0,2pi); the parametrisation is periodic, so PK_SURF_eval works for any value of u, but PK_SURF_parameterise_vector always returns a value in the above range. The range for v is [-pi/2,+pi/2].
The sphere center C, axis A, ref_direction X and radius r can be obtained from PK_SPHERE_ask. The Y axis is the vector product of the sphere axis A and the X axis: Y = A X X. Alternatively, the Y axis can be obtained by evaluating R(pi/2, 0) using PK_SURF_eval and applying the formula.

Figure 38-9 Surface parametrisation - sphere
The parameter u represents longitude; i.e. the angle around the axis, measured from the X axis. It runs clockwise when viewed along the axis. The parameter v represents the latitude; i.e. the angle subtended at the equatorial plane.
A rolling ball blend has a parametric representation of the form:
C( u ) is the spine curve, r is the blend radius. X(u) and Y( u ) are unit vectors such that dC(u)/du, X( u ) and Y( u ) form an orthogonal set. a( u ) is the angle subtended by points on the boundary curves at the spine. X, Y and a are expressed as functions of u, as their values change with u.
The spine of the rolling ball blend is the center line of the blend; i.e. the path along which the center of the ball moves. The range for u is the range for the spine curve and can be output through the PK_BLENDSF_ask function. The range for v is [0,1]. The parameter u represents the progress along the length of the blend. The parameter v runs along a circular arc, with its center on the spine. It takes the value 0 on one boundary, 1 on the other. It is proportional to the angle around the circular arc. If the spine curve is extended by a modeling operation, the parametrisation may also be extended.

Figure 38-10 Surface parametrisation - rolling ball blend
A swept surface has a parametric representation of the form:
C(u) is the section curve, D is the sweep direction (unit vector).
The range for u is the range for the section curve.
The range for v is (-infinity, +infinity).
The section curve and the sweep direction are obtained from PK_SWEPT_ask. The u parameter corresponds to the section curve parameter.
The v parameter represents distance: the distance of the current point from the corresponding point on the section curve.
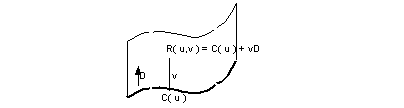
Figure 38-11 Surface parametrisation - swept surface
A spun surface has a parametric representation of the form:
C(u) is the profile curve, Z(u) is the projection of C(u) onto the spin axis. A is the spin axis direction (unit vector)
|
Note:
Z(u) =
P + ( (
C( u ) -
P ) .
A )
A where
P is a reference point on the axis. |
The range for u is the range for the profile curve.
The profile curve C, axis direction A and a reference point P on the axis can be obtained from PK_SPUN_ask

Figure 38-12 Surface parametrisation - spun surface
The u parameter corresponds to the profile curve parameter.
The v parameter represents the angle about the axis, measured from the initial position of the profile curve.
The parameter runs clockwise when viewed along the A axis.
B-surfaces (including B-splines which are represented internally as Bezier) have their own parametrisation.
For details, see Chapter 26, "The Mathematical Form of B-Geometry".
With these parametric geometry evaluation functions it is not necessary for the given parameter to lie within the range specified:
The following functions are handed versions of the functions described in "Evaluation of parametric geometry". These functions give the application control over the direction in which the evaluations are calculated.
| Function | Handed version of |
|---|---|
These functions behave identically to their non-handed equivalents, except at a discontinuity or periodic seam, where the evaluation is approached from the direction indicated by extra handed arguments. Each of these extra arguments can take the following values:
| Value | Description |
|---|---|
|
A left-handed evaluation is approached from below the parameter value |
|
|
A right-handed evaluation is approached from above the parameter value |
The three PK_CURVE functions each take a single additional argument,
hand_direction
, which controls whether evaluation is approached from below (left) or from above (right).
The three PK_SURF functions each take two additional arguments,
u_hand_dir
and
v_hand_dir
. The combination of values for these two arguments, together with the position of the parameter pair, determines the direction from which evaluation is approached, as shown in Figure 38-13.

Figure 38-13 Handed evaluation of parameter pairs on a surface
PK_CURVE_find_vector_interval calculates a parametric interval, given a curve and pair of points lying on it. This is useful when converting Parasolid applications from the old KI interface into the PK interface.
PK_GEOM_is_coincident compares two geometric entities to see if they occupy the same positions in space. Curves running in opposite directions are considered coincident, and so are analytic curves (such as circles) and b-curve if they are identical. The function detects whether the entire surface or curve is coincident with another surface or curve; it does not detect overlaps.
Enquiry functions provide information about entities. They typically have to perform some calculations, and do more than simply output the information which is stored with the entity. Other sections which should be read on this subject are "Geometric output" and "Parametric enquiries" in this chapter, and "Standard representations" in Chapter 39, "Modeling Support".
| Function | Description |
|---|---|
|
To complete a non-axis aligned box bounding a portion of the curve/surface |
|
Two functions that compute non-axis aligned boxes for curves and surfaces. Figure 38-14 illustrates the non-aligned boxing of a B-curve (shown in bold). In this computation there are three non-aligned boxes shown; boxing the whole curve; one third of the curve; then one ninth of the curve. This demonstrates how the non-aligned boxes rapidly diminish in size as the curve is subdivided.

Figure 38-14 Non-aligned boxing vs. aligned boxing
| Function | Description |
|---|---|
This function determines whether a given face is parametrically rectangular. If the face is rectangular the u and v parameters returned lie in the parameter range of the surface given by PK_SURF_ask_uvbox unless the corresponding parameter is periodic. When the parameter is periodic the first parameter of the face lies in the range and the difference between the two parameters does not exceed the period, i.e. the face straddles the boundary of a periodic parameter.
| Function | Description |
|---|---|
|
To find the uvbox which bounds the given face in the parameter space of the face's surface |
Calling PK_SURF_ask_uvbox returns information about the range of values that the parameters u and v can have. A particular face on a surface may be restricted to a smaller range of values. PK_FACE_find_uvbox returns ranges in u and v such that for every point on the face, there is a u, v pair in this range which maps to that point.

The shaded lines represent two possible parameter boxes. The larger box is the one that would include the u,v pairs as returned by PK_SURF_parameterise_vector. The smaller box is the one which is actually returned by PK_FACE_find_uvbox.
| Function | Description |
|---|---|
|
To find a uvbox which bounds the given fin in the parameter space of the fin's owning face's surface |
| Function | Description |
|---|---|
|
To compute the parameter interval of the curve, to which the edge/fin corresponds |
|
In addition, these functions return the unique topological entity of lowest dimensionality belonging to the entity which coincides or contains the point.
| Function | Description |
|---|---|
|
Tests whether two vectors are equal within the current session precision. |
The method you should use to determine whether a face is periodic or not is as follows:
For cylindrical surfaces (or cylindrical like swept surfaces, spun surfaces, or b-surfaces) the face is periodic if there is at least one winding loop (PK_LOOP_ask_type returns PK_LOOP_type_winding_c).
For spherical and toroidal surfaces (or similar spun surfaces or b-surfaces), the face is periodic if there are either no loops, or no loops are outer loops (PK_LOOP_ask_type returns PK_LOOP_type_outer_c).
For conical surfaces (or similar spun surfaces or b-surfaces) the face is periodic if either of the following is true:
You can use PK_FACE_is_coincident to determine whether or not two faces are coincident within a given tolerance. This function receives and returns the following arguments:
| Received | Description |
|---|---|
|
A tolerance within which the faces should be considered coincident |
|
| Returned | Description |
|
A point at which |
For
face1
and
face2
to be considered coincident, both the the following must be true:
If either of these is not true, then the two faces are not coincident.
These restrictions can sometimes mean that faces will not be considered coincident, even when you might expect that they would. For example, consider Figure 38-16, which shows two very similar faces, labeled A and B. The only difference between these faces is that B contains a gap that is smaller than the specified tolerance. However, despite its small size, this gap means that the loops in A and B no longer correspond, and so PK_FACE_is_coincident would not find these faces to be coincident.
PK_FACE_is_coincident may not detect coincidence between faces whose edges are all shorter than the specified tolerance.
Although PK_FACE_is_coincident may fail to find coincidence, it is guaranteed not to find coincidence where there is none.

Figure 38-16 Faces with dissimilar loops are not considered coincident
The information returned in
result
can be one of the following:
| <<< Wire Modeling | Chapters | Modeling Support >>> |