 |
Advanced Surfacing |
| <<< The Mathematical Form of B-Geometry | Chapters | Creation of Extruded Bodies >>> |
Parasolid supports the generation of bodies with freeform geometry by providing functions that perform the following operations:
The resulting body may be either a sheet or a solid, depending on the precise nature of the operation and the bodies used.
The profile is supplied as a single wire or sheet body. If the profile is a wire body then the resulting body is a sheet, if the profile is a sheet body then the result is a solid.
Where the profile is supplied as a wire, the wire body must be oriented (PK_EDGE_propagate_orientation may be used to achieve this). The resulting sheet is constructed so that the outward normal is aligned with the cross product of a tangent in the direction of the profile orientation, and the tangent along the path (taken in that order).
Where the profile is supplied as a sheet, the sheet body may have multiple laminar boundaries, but should not be disjoint. Sweeps of profiles with multiple laminar boundaries along closed paths result in solids with internal voids, as shown in Figure 27-1.

Figure 27-1 Performing a sweep using a sheet profile with two laminar boundaries
None of the profile's geometry or topology appears in the resulting solid. It is the application's responsibility to delete the profile when it is no longer required.
The path is supplied as a wire body. The wire must be manifold and should be oriented (using PK_EDGE_propagate_orientation). The sweep direction follows the direction of the wire. The path wire should not contain any tolerant edges or vertices. The path need not be smooth. Non-G1 continuous corners in the path produce mitred corners in the resulting swept body.
If the path is a closed wire, then the start vertex should be specified in the
path_start
argument. If the path is open then a start vertex need not be supplied, in which case the sweep starts from the first vertex of the oriented path wire. If a start vertex is specified, it may be at any point on the path wire, but should correspond to the position of the profile. If the start vertex is at a sharp corner in the path, then orientation of the profile to the path is taken from the edge following the start vertex on the oriented path wire, where such an edge exists. The path wire must contain at least one vertex.

Figure 27-2 Mitred corners (right) produced from non-G1 continuous corners in the path (left)
None of the path's geometry or topology appears in the resulting solid. It is the application's responsibility to delete the path when it is no longer required.
|
Note: Different start vertices can produce very different results using the same path and profile. |
The alignment options control the orientation of the profile as it moves along the path. The application can choose to either keep the orientation constant, or vary the orientation along the sweep to follow the shape of the path.
The control is made through the
alignment
field of the structure passed to the received
options
argument. This field should be set to either of the following values:
| Option | Orientation |
|---|---|

If the
alignment
option is specified as normal, Parasolid adjusts its frame of reference at any G2 discontinuity in the sweep path to maintain continuity of the resulting surfaces.
The twist option controls the rotation of the profile as it moves along the path. This can be controlled by supplying one of the following:
The twist is performed by applying a rotational transformation to the profile as it moves along the path. Twist cannot be applied along a non-smooth path.

The scale options controls the variation in the size of the profile as it moves along the path. This can be controlled by supplying one of the following:
The scale is performed by applying a scaling transformation to the profile as it moves along the path. Scale cannot be applied along a non-smooth path.

In specifying these laws you must remember that all sweeps are carried out making transformations, including scale and twist, on the profile about the appropriate location on the path.
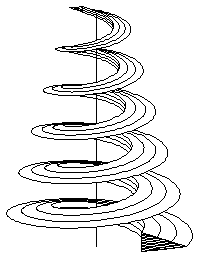
Figure 27-6 Sweep with scale and twist
The topology form options control how faces should divide up the resulting body. The choices are to produce:
The control is made via the
topology_form
field of the structure passed to the received
options
argument. This field should be set to one of the following values:
| Value | Description |
|---|---|
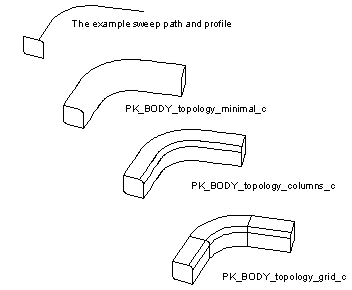
Figure 27-7 Sweeping topology form
The simplify options allow the application to control whether the surfaces of the resultant body should all be B-surfaces or whether they should be simplified to analytics where possible. Simplification is performed on the entire surface of each face and does not alter the topology of the resultant body.
The control is made through the
simplify
field of the structure passed to the received
options
argument. This field should be set to one of the following values:
| Value | Description |
|---|---|
The resultant bodies produced by PK_BODY_make_swept_body have nominal curves enabled.
Edges running parallel to the profile have nominal curves on them derived from the profile geometries. The nominal curves are copies of the (nominal) curves of the profile edges, transformed along the path.
Lateral edges, i.e. edges running in the direction of the sweep, have nominal geometry derived from the surfaces of their adjacent faces. In general they are B-curves, though analytic curves may be produced when the
simplify
option is set to PK_BODY_simplify_yes_c.
When a sweep results in a body that intersects itself, Parasolid attempts to repair the body to produce a valid solid. This may involve splitting faces; however, the tracking information returned reflects the final state of the body. Locally self-intersecting surfaces and clashes between adjacent faces are not repaired. Figure 27-8 shows two examples of bodies that intersect themselves, that have been successfully repaired by the sweep operation.

Figure 27-8 Repairs to self-intersecting faces created during sweep operations
You can use the
fair
option in PK_BODY_make_swept_body_o_t to improve the method of the sweep along the path. This takes the following values:
| Value | Description |
|---|---|
|
Do not twist the orientation of the profile along regions of the path that either: |
This is illustrated in Figure 27-9.

Figure 27-9 Removing undesirable twisting in sweep operations
Lofting creates a sheet or solid body by fitting surfaces through a series of profiles, and is performed by PK_BODY_make_lofted_body.
You can additionally constrain the geometry of a loft across profiles, by specifying any of the following:
A series of options controls the derivative conditions, and how adjacent profiles containing different numbers of edges are matched.
The profiles are supplied as an array of wire, sheet or minimal bodies. If either of the end profiles are wires then the resulting body is a sheet, otherwise the result is a solid.
The profiles supplied must be either all open or all closed. Mixing open and closed profiles is not permitted. Minimum body profiles are considered to be open or closed depending on the closure of the other supplied profiles.
Where the profiles are supplied as wires:
The resulting sheet is constructed so that the outward normal is aligned with the cross product of a tangent in the direction of the profile orientation, and the loft direction (taken in that order). All the profiles should have the same orientation in order to avoid twist in the result.
Where the profiles are supplied as sheets:
Sheets and minimum bodies can only be used as start or end profiles. Intermediate profiles must be wire bodies.
A start vertex must be supplied for each profile. The start vertices for the profiles should be aligned to avoid twist in the result, as shown in Figure 27-10.
None of the profiles' geometry or topology appears in the resulting solid. It is the application's responsibility to delete the profiles when they are no longer required.

Parasolid provides several different methods of controlling the derivative conditions to be applied to the start and end profiles of a loft. These are specified using structures and fields in the
end_conditions
structure of PK_BODY_make_lofted_body_o_t. The
end_conditions
structure contains the following options:
| Option | Description |
|---|---|
|
If PK_PARAM_periodic_yes_c, the loft returns periodically to the start profile. If the start profile is a sheet then the result is a solid body. Otherwise the result is a sheet. |
|
|
A structure that specifies a derivative condition for the start profile in the loft. See Section 27.3.4, "Specifying derivative conditions" for a description of the fields available in this structure. |
|
|
A structure that specifies a derivative condition for the end profile in the loft. See Section 27.3.4, "Specifying derivative conditions" for a description of the fields available in this structure. If the loft is periodic, these constraints are ignored. |

Figure 27-11 Derivative conditions for the start and end profiles in a loft
In addition to the start and end profiles in a loft (as described in Section 27.3.2), you can specify derivative conditions to control the shape of the loft at any other profile. This is done using the following options to specify derivative conditions for any combination of other profiles in a loft:
| Option | Description |
|---|---|
|
The number of profiles that you want to specify derivative conditions for. This is the number of elements in both the |
|
|
An array of derivative conditions for the profiles indexed in |
|
|
An array of integers. Each integer refers to a profile in the loft. See "Specifying intermediate profiles" |
The
intermediate_derivs
option contains an array of derivative conditions for the profiles you want to constrain. Each element in the array describes a curvature and clamp type to apply to the loft at a given profile. This is specified using a structure in the same way as derivative conditions for the start and end profiles in a loft. See Section 27.3.4, "Specifying derivative conditions" for more information.
Derivative conditions specified in
intermediate_derivs
are mapped onto profiles in the loft using the
intermediate_profiles
array. This is an array of integers that specifies which profile each derivative condition should be applied to.
The start and end profiles must not be referred to in the
intermediate_profiles
array. It must therefore contain integers between
where
n_profiles
is the number of profiles, as specified in the call to PK_BODY_make_lofted_body.
Figure 27-12illustrates how derivative conditions can be specified for some of the intermediate profiles in a loft containing 6 profiles.

Figure 27-12 Specifying derivative conditions for intermediate profiles in a loft
You specify derivative conditions for a loft operation using a PK_BODY_loft_deriv_conds_t structure. Derivative conditions can be applied to any of the following:
These fields are also used to specify derivative conditions for any intermediate profile in a loft.
| Option | Description |
|---|---|
|
If PK_BODY_loft_unconstrained_c, no constraints are applied to the curvature across the profile or guide wire. This is the default. If PK_BODY_loft_natural_c, natural (zero) curvature is applied across the profile. This may not be used with vector, face, or planar clamps. You cannot use natural curvature on any of the following: When natural curvature is used on either end of a non-periodic loft, no other derivative conditions may be specified for that profile. |
|
|
The type of clamp to be supplied. This can be one of vector, face, planar, or none. |
|
|
With a vector clamp, a tangent vector is applied to vertices of the profile or guide wire to constrain the tangents across that profile or guide wire. You can supply separate pairs of tangent vectors and vertices for each vertex you want to constrain, or you can supply a single tangent vector to be applied across the whole profile or guide wire. Both the magnitude and direction of the tangent vectors is matched. |
|
|
With a face clamp, the tangents across the profile or guide wire are constrained to match faces that meet the profile or guide wire. You should supply pairs of clamp faces and profile or guide edges for the edges you want to constrain. You can specify the magnitude for the cross boundary derivative, paired with any vertex from an edge with a face clamp, as shown in Figure 27-13. |
|
|
With a planar clamp, the start or end of the loft is clamped parallel to a specified plane. The magnitude of the cross boundary derivative can also be specified. See Figure 27-14 for an example of planar clamping. |

Figure 27-13 Partial face clamps with different cross boundary derivative magnitudes
|
Note: If you are using guide wires, then the use of certain derivative conditions is restricted. See "Lofting with guide wires" for full details. |
Lofting to a degenerate profile is considered as having a loft profile which occupies a single point in space. A degenerate point profile is specified as a minimal body.
Three types of end conditions are applicable at a degenerate loft profile:
In the latter case, the order in which the vectors are supplied is significant: the first tangent vector in the clamp is associated with the start vertex of the adjacent profile, and the remaining tangent vectors are applied in order along the adjacent profile. Mismatching these can cause the loft to twist.

Figure 27-14 Lofting degenerate profiles
Where all the profiles in the loft have the same number of edges, and hence the same number of vertices, the vertices are mapped one-to-one across the profiles. All start vertices are matched with each other, then subsequent vertices on each profile are matched in order (i.e. nth vertices are matched).
Where the profiles have different numbers of edges, the application needs to provide information on how to match the profiles. This is done in one of two ways:
If a mapping between vertices is provided, constraints must be followed:
Figure 27-15 gives some examples of vertex mappings that are not possible in Parasolid.

Figure 27-15 Illegal vertex mapping
The topology form options control how faces should divide up the resulting body. The choices are to produce:
The control is made via the
topology_form
field of the structure passed to the received
options
argument. This field should be set to one of the following values:
| Value | Description |
|---|---|
|
Note: Using guide wires (see Section 27.3.10, "Lofting with guide wires") does not change the number of faces in the resulting body, no matter which topology form option is used. |

Figure 27-16 Lofting topology form
The simplify options allow the application to control whether the surfaces of the resultant body should all be B-surfaces or whether they should be simplified to analytics where possible. Simplification is performed on the entire surface of each face and does not alter the topology of the resultant body.
The control is made through the
simplify
field of the structure passed to the received
options
argument. This field should be set to one of the following values:
| Value | Description |
|---|---|
The resultant bodies produced by PK_BODY_make_lofted_body have nominal curves enabled.
Edges running parallel to the profile(s) have nominal curves on them derived from the profile geometries. The nominal curves are copies of the (nominal) curves of the edges of the corresponding profile.
Lateral edges, i.e. edges running in the direction of the loft, have nominal geometry derived from the surfaces of their adjacent faces. In general they are B-curves, though analytic curves may be produced when the
simplify
option is set to PK_BODY_simplify_yes_c.
By specifying guide wires for a loft operation, you can constrain the loft geometry across profiles, resulting in a lofted body that follows the shape described by the guide wires at relevant points. Figure 27-17 shows the effect of specifying a guide wire during a lofting operation. In the example, both end profiles are wires, thereby producing a sheet as the result. The guide wire specified is a half circle that intersects both profiles at a point one third from the left of each profile. The resulting body follows the guide wire along the line of the guide wire itself, and follows the shape of the loft operation at the ends of the profiles. In between, it transitions smoothly to result in the body shown in the right hand part of the figure.
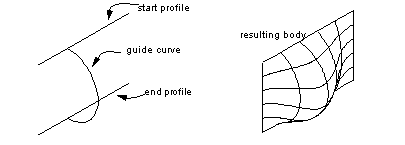
Figure 27-17 Use of a simple guide wire during a lofting operation
Guide wires must be G1-continuous and are interpolated by the loft as iso-parameter curves along the loft direction. Each guide wire has a region of influence that covers the whole length of the loft and whose bound is the boundary of the corresponding smooth section of profiles or (in cases where more than one guide wire is specified) adjacent guide wires, whichever is reached first.
Each guide wire is assumed to intersect every profile once only at corresponding vertices, subject to the largest vertex tolerance there. Guide wires must be oriented and bound by their intersections with the start and end profiles.
If any one of a set of matched profile vertices lies on a guide wire, then they must all lie on the same guide wire. This is illustrated in Figure 27-18. On the left hand side of the figure three profiles are shown, A, B, and C, in which the highlighted vertices form a set of matching profile vertices. The guide curve shown correctly passes through each of these vertices. The right hand side of Figure 27-18 shows the same three profiles, but for two profiles (B and C) the guide curve passes through vertices that are not in the set of matching vertices. The loft operation described in the right hand side of the figure could not be performed.

Figure 27-18 Correct and incorrect use of guide wires with matching profile vertices
Guide wires restrict the use of certain clamped derivative conditions. Because guide wires are interpolated by the loft operation, the loft derivatives along the guide wires are completely determined. Any clamped end condition must therefore satisfy both the tangency and the derivative magnitude imposed by the guide wires. This means that the following clamp operations are not allowed at any profile vertex that has a match on a guide wire:
Edges of the lofted body that are coincident with the guide wire(s) have nominal curves on them that are derived from the guide wire geometries. These nominal curves are copies of the (nominal) curves of the edges of the corresponding guide wire.
Control of guide wires is made through the
n_guide_wires
and
guide_wires
fields passed to the received
options
argument in PK_BODY_make_lofted_body:
| Option | Description |
|---|---|
|
An integer specifying the number of guide curves being used. |
|
In addition to loft profiles (as described in Section 27.3.2 and Section 27.3.3), you can specify derivative conditions to control the shape of the lofted body along any guide wire specified, as shown in Figure 27-19.

Figure 27-19 Applying derivative conditions to guide wires
Derivative conditions are applied to guide wires using the following options to PK_BODY_make_lofted_body:
| Option | Description |
|---|---|
|
The number of guide wires that you want to specify derivative conditions for. This is the number of elements in both the |
|
|
An array of derivative conditions for the guide wires indexed in |
|
|
An array of integers. Each integer refers to a guide wire in the loft, where 0 refers to the first guide wire specified in the |
These options are analogous to the options used to specify derivative conditions for intermediate profiles, as described in Section 27.3.3.
|
Note: When supplying derivative conditions for guide wires, the following clamp operations are not allowed at any guide vertex that has a match on a profile: |
You can extend surfaces of any class (except foreign geometry surfaces) using PK_SURF_extend. This function take as its arguments a surface to modify and an options structure that specifies the type of extension required. It returns a status flag that indicates the outcome of the operation.
You can extend a surface in any of four ways:
|
Note: Rational B-surfaces are only implicitly extended. |

Figure 27-20 Extending a surface (a) to a specified point (b) to a specified box
Each type is specified using fields in the options structure, as described in the table below. The default values for these fields are set such that no extension is performed to a surface supplied to PK_SURF_extend.
For each of the
x
_ratio
options, a ratio of 1.0 extends the relevant boundary by 100%. The effect of extending different boundaries by different amounts is shown in Figure 27-21.

Figure 27-21 Extending a surface by ratio
The effect of setting
allow_partial_extension
is shown in Figure 27-22. In the example shown, extending the specified surface to the point shown would result in a self-intersection, thereby creating an invalid surface.
allow_partial_extension
is PK_LOGICAL_false, then no extension is performed.
allow_partial_extension
is PK_LOGICAL_true, then the surface is extended as far as the point of self-intersection, as indicated in the illustration.
Figure 27-22 Partially extending a surface that would otherwise be invalid
PK_SURF_extend returns a status flag to indicate the result of the operation. This can take the following values:
Spirals, helices, and tapered helices are all created using the same basic principles. For each shape, a point or a curve is swept several times about an axis in a circular motion. The distance of the point or curve from the axis, together with its distance along the axis, determine the nature of the final shape, allowing shapes such as those shown in Figure 27-23. All these shapes can be referred to as a general helix.

Figure 27-23 Examples of general helical curves and surfaces
All general helices have the following common properties, illustrated in Figure 27-24:

Figure 27-24 Anatomy of a general helix
You can create a general helix using the following functions:
| Function | Description |
|---|---|
|
Sweep a point about an axis, so as to produce a helical curve |
|
|
Sweep a curve about an axis, so as to produce a helical surface |
Both of these functions take a very similar set of arguments:
| Argument | Description |
|---|---|
|
A reference point for a helical curve. The helix need not include the point itself. |
|
|
A curve from which a section is used to create a helical surface |
|
|
The section of |
|
|
|
|
The number of turns that the helix makes, expressed as an interval. The supplied
For tapered helices, |
|
|
The helical pitch of the helix. If this is 0, then a spiral is created. |
|
|
The spiral pitch of the helix. If this is 0, then the helix does not taper. If this is a negative number, then the helix tapers inwards; if positive, the helix tapers outwards. For helices that taper inwards, the spiral pitch must be consistent with the number of turns requested, so as to ensure that the helix does not cross the axis. See Section 27.5.4, "Controlling inward taper" for details. |
|
|
Note: Arguments marked with * apply only to PK_POINT_make_helical_curve. Arguments marked with ** apply only to PK_CURVE_make_helical_surf. |
The
point
supplied to PK_POINT_make_helical_curve and PK_CURVE_make_helical_surf is a reference point that is used to determine the path of the resulting helix. In particular, it does
not necessarily represent a start point or end point for the helix - indeed, the resulting helix need not pass through
point
at all.
You use the
turns
interval to express how the helix should be formed "around"
point
:
point
is always taken to lie at 0 in
turns
, allowing you to create helices such as those described below:
| Turns | Helix created |
|---|---|
|
starts at -X and ends at X, with point in the middle of the path |
|
|
starts at x and ends at X, so that point is not contained in the helix at all. |
The effect that different values of
turns
have on helices created from the same reference point is illustrated in Figure 27-25.

Figure 27-25 Using
turns
to create different helices for a single reference point
Two combinations of values make a general helix taper inwards, as opposed to outwards:
turns
interval, combined with a negative
spiral_pitch
.
turns
interval, combined with a positive
spiral_pitch
.In either case, the helix can only taper inwards as far as the axis itself: any attempt to create a helix that tapers further than this results in the error PK_ERROR_bad_parameter.
To ensure that an inward-tapering helix is valid, the following must both be true:
turn
spiral_pitch
The following table shows a range of valid and invalid spirals. The invalid spirals would raise the error PK_ERROR_bad_parameter.
| Valid spirals | Invalid spirals |
|---|---|
| <<< The Mathematical Form of B-Geometry | Chapters | Creation of Extruded Bodies >>> |