Smooth Edge Sequencing
The API api_smooth_edge_seq and Scheme extension blend:get-smooth-edges have been provided to predict the extent of the blend sequence in the form of the list of edges, covered by the blend faces made by a ball rolling freely on the support faces. It uses the following algorithm to calculate prediction.
Given a seed edge, ACIS considers all non-smooth edges (that is, edges for which the normals of the adjacent faces are not parallel) smoothly connected (that is, the tangent directions of the two edges at the common vertex are parallel) at the start and at the end vertices of this edge. The sequence is constructed by adding new edges to the beginning and the end of the collected list of edges, based on the examination of the current head and tail vertices.
The different situations of edges meeting at the vertex are discussed below (in all the diagrams, the red edge shows the last edge in the smoothly-connected list and the green edge is being considered for adding to the list).
Situation 1
There are only two smoothly connected non-smooth edges of the same convexity coming to a vertex. Smooth-edge sequence will propagate over such a vertex to the adjacent edge. In such a case, the vertex will be removed by ACIS and the resulting blend face will have no indications that the original edges had a vertex at this location.
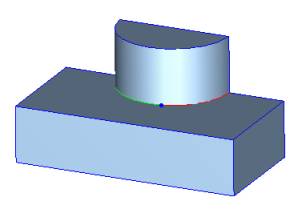
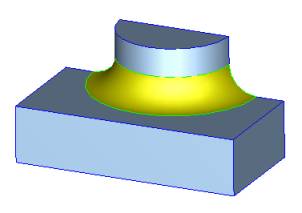
Situation 2
There are only two smoothly connected non-smooth edges of different convexity coming to a vertex. This means that, at the common vertex, the adjacent surface normals are parallel, indicating that the two edges are smooth at the vertex but become convex and concave going away from the vertex (that is, the vertex was introduced to mark convexity change along the intersection of the two surfaces). Smooth-edge sequence stops at such a vertex.
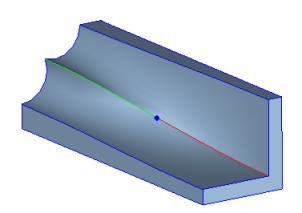
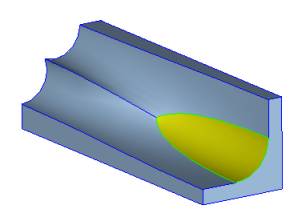
Situation 3
The two non-smooth edges coming to a vertex are not smoothly connected. This can only happen if at least one of the adjacent faces has a G1 discontinuous surface and there is no edge at the crease (such body cannot be constructed in ACIS but may be exported from other modelers). Such situation is not supported.
Situation 4
There are more than two edges coming to a vertex. Two non-smooth edges of the same convexity are smoothly connected and the remaining edges are smooth ("slant edges"). Smooth-edge sequence will propagate over such a vertex to the adjacent edge. The resulting blend faces will be smoothly connected across the isoparametric cross-edges, starting at the positions where the spring curves intersect the lateral edges.
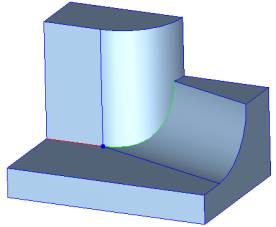
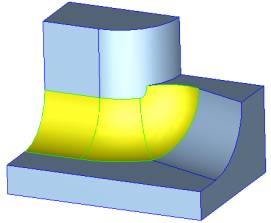
Situation 5
There are more than two edges coming to a vertex. Two non-smooth edges of the same convexity are smoothly connected and some of the remaining edges are non-smooth. Smooth-edge sequence will stop at such a vertex. If the blend needs to extend beyond such a vertex, the remaining edges have to be selected separately (for example user can call api_smooth_edge_seq again with a different seed edge). The resulting blend faces will be mitered between the points where the spring curve(s) intersect the non-smooth unblended edge(s).
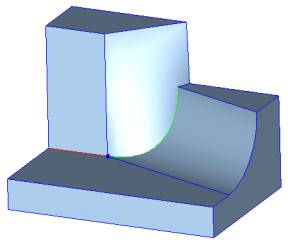
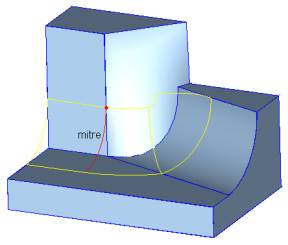
Situation 6
Several edges are coming to a vertex and none of them is smoothly connected to the current blended edge. Smooth-edge sequence will stop at such a vertex. If the blend needs to extend further, the remaining edges have to be selected separately.
Limitations
The limitations api_smooth_edge_seq are closely related to the limitations of the edge-based blending approach as a whole: one-to-one correspondence between blended edges and blend faces often cannot be established.
Evident examples of the failure of edge-based blending paradigm, where the use of edges as the indication of the blend extent becomes meaningless are:
- Blend supports are different from the faces adjacent to the blended edges.
- Slant lateral edges cause the extent of the blend faces to be substantially different from that of the blended edges: some edges may not have corresponding blend faces, while some blend faces may cover multiple edges.
- Geometry of the support surfaces is considerable different along the blend edge and the blend spring curve.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.