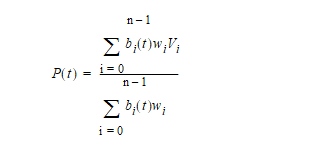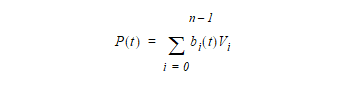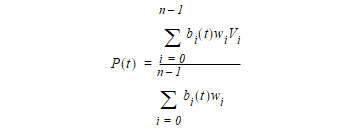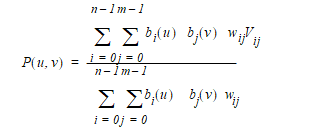Schema Definitions

5.1 Underlying types

union CURVE_OWNER_u

     struct EDGE_s                *edge;

     struct HALFEDGE_s            *halfedge;

     struct BODY_s                *body;

     struct ASSEMBLY_s            *assembly;

     struct WORLD_s               *world;

};

typedef union CURVE_OWNER_u CURVE_OWNER;

union SURFACE_OWNER_u

     struct FACE_s                *face;

     struct BODY_s                *body;

     struct ASSEMBLY_s            *assembly;

     struct WORLD_s               *world;

};

typedef union SURFACE_OWNER_u SURFACE_OWNER;

union ATTRIB_FEAT_u

     struct ATTRIBUTE_s           *attribute;

     struct FEATURE_s             *feature;

     struct MEMBER_OF_FEATURE_s   *member_of_feature;

};

typedef union ATTRIB_FEAT_u ATTRIB_FEAT;

[back to top]

5.2 Geometry

union CURVE_u

     struct LINE_s                *line;

     struct CIRCLE_s              *circle;

     struct ELLIPSE_s             *ellipse;

     struct INTERSECTION_s        *intersection;

     struct TRIMMED_CURVE_s       *trimmed_curve;

     struct PE_CURVE_s            *pe_curve;

     struct B_CURVE_s             *b_curve;

     struct SP_CURVE_s            *sp_curve;

     struct POLYLINE_s            *polyline;

};

typedef union CURVE_u      CURVE;

union SURFACE_u

     struct PLANE_s               *plane;

     struct CYLINDER_s            *cylinder;

     struct CONE_s                *cone;

     struct SPHERE_s              *sphere;

     struct TORUS_s               *torus;

     struct BLENDED_EDGE_s        *blended_edge;

     struct BLEND_BOUND_s         *blend_bound;

     struct OFFSET_SURF_s         *offset_surf;

     struct SWEPT_SURF_s          *swept_surf;

     struct SPUN_SURF_s           *spun_surf;

     struct PE_SURF_s             *pe_surf;

     struct B_SURFACE_s           *b_surface;

     struct MESH_s                *mesh;

};

typedef union SURFACE_u    SURFACE;

union GEOMETRY_u

     struct LATTICE_s             *lattice;

     union SURFACE_u               surface;

     union CURVE_u                 curve;

     struct POINT_s               *point;

     struct TRANSFORM_s           *transform;

};

typedef union GEOMETRY_u GEOMETRY;

5.2.1 Curves

In the following field tables, ‘pointer0’ means a reference to another node which may be null. ‘pointer’ means a non-null reference.

All curve nodes share the following common fields:

Field Name	Data Type	Description
`node_id`	int	Integer value unique to curve in part
`attributes_features`	pointer0	Attributes and featuresassociated with any curve
`owner`	pointer0	topological owner
`next`	pointer0	next curve in geometry chain
`previous`	pointer0	previous curve in geometry chain
`geometric_owner`	pointer0	geometric owner node
`sense`	char	sense of curve “+” or “-” (see end of Geometry section)

struct ANY_CURVE_s              //Any Curve

    int                           node_id;              // $d

    union  ATTRIB_FEAT_u          attributes_features;  // $p

    union  CURVE_OWNER_u          owner;                // $p

    union  CURVE_u                next;                 // $p

    union  CURVE_u                previous;             // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;      // $p

    char                          sense;                // $c

};

typedef struct ANY_CURVE_s *ANY_CURVE;

5.2.1.1 Line

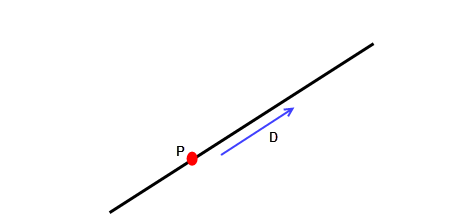
A straight line has a parametric representation of the form:

R(t) = P + t D

Where:

P is a point on the line
D is its direction

Field Name	Data Types	Description
`pvec`	vector	point on the line
`direction`	vector	direction of the line (a unit vector)

struct LINE_s == ANY_CURVE_s      //Straight line

    int                           node_id;              // $d

    union  ATTRIB_FEAT_u          attributes_features;  // $p

    union  CURVE_OWNER_u          owner;                // $p

    union  CURVE_u                next;                 // $p

    union  CURVE_u                previous;             // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;      // $p

    char                          sense;                // $c

    vector                        pvec;                 // $v

    vector                        direction;            // $v

};

typedef struct LINE_s       *LINE;

5.2.1.2 Circle

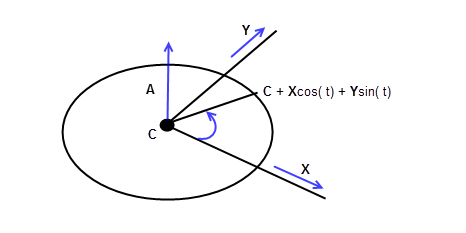
A circle has a parametric representation of the form:

R(t) = C + r X cos(t) + r Y sin(t)

Where:

C is the centre of the circle
r is the radius of the circle
X and Y are the axes in the plane of the circle

Field Name	Data Type	Description
`centre`	vector	Centre of circle
`normal`	vector	Normal to the plane containing the circle (a unit vector)
`x_axis`	vector	X axis in the plane of the circle (a unit vector)
`radius`	double	Radius of circle

The Y axis in the definition above is the vector cross product of the normal and x_axis .

struct CIRCLE_s == ANY_CURVE_s    //Circle

    int                           node_id;              // $d

    union  ATTRIB_FEAT_u          attributes_features;  // $p

    union  CURVE_OWNER_u          owner;                // $p

    union  CURVE_u                next;                 // $p

    union  CURVE_u                previous;             // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;      // $p

    char                          sense;                // $c

    vector                        centre;               // $v

    vector                        normal;               // $v

    vector                        x_axis;               // $v

    double                        radius;               // $f

};

typedef struct CIRCLE_s    *CIRCLE;

5.2.1.3 Ellipse

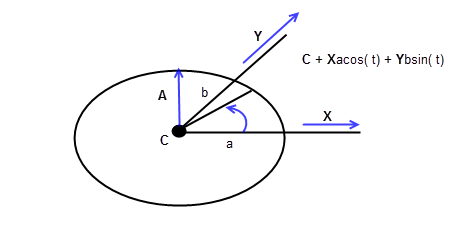
An ellipse has a parametric representation of the form:

R(t) = C + a X cos(t) + b Y sin(t)

Where:

C is the centre of the ellipse
X is the major axis
a is the major radius
Y and b are the minor axis and minor radius respectively

Field Name	Data Type	Description
`centre`	Vector	Centre of ellipse
`normal`	Vector	Normal to the plane containing the ellipse (a unit vector)
`x_axis`	Vector	major axis in the plane of the ellipse (a unit vector)
`major_radius`	Double	major radius
`minor_radius`	Double	minor radius

The minor axis (Y) in the definition above is the vector cross product of the normal and x_axis .

struct ELLIPSE_s == ANY_CURVE_s   //Ellipse

    int                           node_id;              // $d

    union  ATTRIB_FEAT_u          attributes_features;  // $p

    union  CURVE_OWNER_u          owner;                // $p

    union  CURVE_u                next;                 // $p

    union  CURVE_u                previous;             // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;      // $p

    vector                        centre;               // $v

    char                          sense;                // $c

    vector                        normal;               // $v

    vector                        x_axis;               // $v

    double                        major_radius;         // $f

    double                        minor_radius;         // $f

};

typedef struct ELLIPSE_s   *ELLIPSE;

5.2.1.4 B_CURVE (B-spline curve)

XT supports B-spline curves in full NURBS format. The mathematical description of these curves is:

Non Uniform Rational B-splines as (NURBS), and

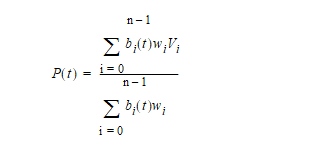
the more simple Non Uniform B-spline

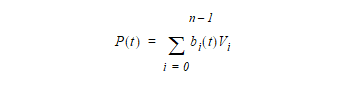
Where:

n = number of vertices (n_vertices in the PK standard form)

V0 ...Vn-1 are the B-spline vertices

w0 ...wn-1 are the weights

bi (t),i = 0...n-1 are the B-spline basis functions

KNOT VECTORS

The parameter t above is global. The user supplies an ordered set of values of t at specific points. The points are called knots and the set of values of t is called the knot vector. Each successive value in the set shall be greater than or equal to its predecessor. Where two or more such values are the same to angular resolution we say that the knots are coincident, or that the knot has multiplicity greater than 1. In this case it is best to think of the knot set as containing a null or zero length span. The principal use of coincident knots is to allow the curve to have less continuity at that point than is formally required for a spline. A curve with a knot of multiplicity equal to its degree can have a discontinuity of first derivative and hence of tangent direction. This is the highest permitted multiplicity except at the first or last knot where it can go as high as (degree+1).

In order to avoid problems associated, for example with rounding errors in the knot set, XT stores an array of distinct values and an array of integer multiplicities. This is reflected in the standard form used by the PK for input and output of B-curve data.

Most algorithms in the literature, and the following discussion refer to the expanded knot set in which a knot of multiplicity n appears explicitly n times.

THE NUMBER OF KNOTS AND VERTICES

The knot set determines a set of basis functions which are bell shaped, and non zero over a span of (degree+1) intervals. One basis function starts at each knot, and each one finishes (degree+1) knots higher. The control vectors are the coefficients applied to these basis functions in a linear sum to obtain positions on the curve. Thus it can be seen that we require the number of knots n_knots = n_vertices + degree + 1 .

THE VALID RANGE OF THE B-CURVE

So if the knot set is numbered {t0 to tn_knots-1 } it can be seen then that it is only after tdegree that sufficient (degree+1) basis functions are present for the curve to be fully defined, and that the B-curve ceases to be fully defined after tn_knots - 1 - degree.

The first degree knots and the last degree knots are known as the imaginary knots because their parameter values are outside the defined range of the B-curve.

PERIODIC B-CURVES

When the end of a B-curve meets its start sufficiently smoothly XT allows it to be defined to have periodic parameterisation. That is to say that if the valid range were from tdegree to tn_knots - 1 - degree then the difference between these values is called the period and the curve can continue to be evaluated with the same point reoccurring every period.

The minimal smoothness requirement for periodic curves in XT is tangent continuity to angular resolution, but we strongly recommend Cdegree-1, or continuity in the (degree-1)th derivative. This in turn is best achieved by repeating the first degree vertices at the end, and by matching knot intervals so that counting from the start of the defined range, tdegree, the first degree intervals between knots match the last degree intervals, and similarly matching the last degree knot intervals before the end of the defined range to the first degree intervals.

CLOSED B-CURVES

A periodic B-curve shall also be closed, but it is permitted to have a closed B-curve that is not periodic.

In this case the rules for continuity are relaxed so that only C0 or positional continuity is required between the start and end. Such closed non-periodic curves are not able to be attached to topology.

RATIONAL B-CURVE

In the rational form of the curve, each vertex is associated with a weight, which increases or decreases the effect of the vertex without changing the curve hull. To ensure that the convex hull property is retained, the curve equation is divided by a denominator which makes the coefficients of the vertices sum to one.

Where w0 ... wn-1 are weights.

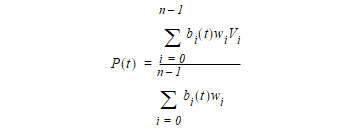
Each weight may take any positive value, and the larger the value, the greater the effect of the associated vertex. However, it is the relative sizes of the weights which is important, as may be seen from the fact that in the equation given above, all the weights may be multiplied by a constant without changing the equation.

In XT the weights are stored with the vertices by treating these as having an extra dimension. In the usual case of a curve in 3-d cartesian space this means that vertex_dim is 4, the x, y, z values are multiplied through by the corresponding weight and the 4th value is the weight itself.

struct B_CURVE_s == ANY_CURVE_s   //B curve

    int                           node_id;              // $d

    union  ATTRIB_FEAT_u          attributes_features;  // $p

    union  CURVE_OWNER_u          owner;                // $p

    union  CURVE_u                next;                 // $p

    union  CURVE_u                previous;             // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;      // $p

    char                          sense;                // $c

    struct NURBS_CURVE_s         *nurbs;                // $p

    struct CURVE_DATA_s          *data;                 // $p

};

typedef struct B_CURVE_s     *B_CURVE;

The data stored in the XT data for a NURBS_CURVE is

Field Name	Data Type	Description
`degree`	Short	degree of the curve
`n_vertices`	Int	number of control vertices (“poles”)
`vertex_dim`	Short	dimension of control vertices
`n_knot`	Int	number of distinct knots
`knot_type`	Byte	form of knot vector
`periodic`	Logical	true if curve is periodic
`closed`	Logical	true if curve is closed
`rational`	Logical	true if curve is rational
`curve_form`	Byte	shape of curve, if special
`bspline_vertices`	Pointer	control vertices node
`knot_mult`	Pointer	knot multiplicities node
`knot`	Pointer	knots node

The knot_type enum is used to describe whether or not the knot vector has a certain regular spacing or other common property:

typedef enum

    SCH_unset = 1,             //Unknown

    SCH_non_uniform = 2,       //Known to be not special

    SCH_uniform = 3,           //Uniform knot set

    SCH_quasi_uniform = 4,     //Uniform apart from bezier ends

    SCH_piecewise_bezier = 5,  //Internal multiplicity of

                                 order-1

    SCH_bezier_ends = 6        //Bezier ends, no other property

    SCH_knot_type_t;

A uniform knot set is one where all the knots are of multiplicity one and are equally spaced. A curve has bezier ends if the first and last knots both have multiplicity ‘order’.

The curve_form enum describes the geometric shape of the curve. The parameterisation of the curve is not relevant.

typedef enum

    SCH_unset          = 1,     //Form is not known

    SCH_arbitrary      = 2,     //Known to be of no particular

                                  shape

    SCH_polyline       = 3,

    SCH_circular_arc   = 4,

    SCH_elliptic_arc   = 5,

    SCH_parabolic_arc  = 6,

    SCH_hyperbolic_arc = 7

    SCH_curve_form_t;

struct NURBS_CURVE_s             //NURBS curve

    short                          degree;              // $n

    int                            n_vertices;          // $d

    short                          vertex_dim;          // $n

    int                            n_knots;             // $d

    SCH_knot_type_t                knot_type;           // $u

    logical                        periodic;            // $l

    logical                        closed;              // $l

    logical                        rational;            // $l

    SCH_curve_form_t               curve_form;          // $u

    struct BSPLINE_VERTICES_s     *bspline_vertices;    // $p

    struct KNOT_MULT_s            *knot_mult;           // $p

    struct KNOT_SET_s             *knots;               // $p

};

typedef struct NURBS_CURVE_s *NURBS_CURVE;

The bspline vertices node is simply an array of doubles; vertex_dim doubles together define one control vertex. Thus the length of the array is n_vertices * vertex_dim .

struct BSPLINE_VERTICES_s        // B-spline vertices

    double                 vertices[ 1 ];               // $f[]

};

typedef struct BSPLINE_VERTICES_s *BSPLINE_VERTICES;

The knot vector of the NURBS_CURVE is stored as an array of distinct knots and an array describing the multiplicity of each distinct knot. Hence the two nodes:

struct KNOT_SET_s                //Knot set

    double                 knots[ 1 ];                  // $f[]

};

typedef struct KNOT_SET_s *KNOT_SET;

and

struct KNOT_MULT_s               //Knot multiplicities

    short                  mult[ 1 ];                   // $n[]

};

typedef struct KNOT_MULT_s *KNOT_MULT;

The data stored in the XT data for a CURVE_DATA node is:

typedef enum

    SCH_unset                     = 1,  //check has not been

                                         performed

    SCH_no_self_intersections     = 2,  //passed checks

    SCH_self_intersects           = 3,  //fails checks

    SCH_checked_ok_in_old_version = 4  //see below

    SCH_self_int_t;

struct CURVE_DATA_s  //curve_data

    SCH_self_int_t               self_int;              // $u

    Struct HELIX_CU_FORM_s      *analytic_form          // $p

};

typedef struct CURVE_DATA_s *CURVE_DATA;

The self-intersection enum describes whether or not the geometry has been checked for self-intersections, and whether such self-intersections were found to exist:

The SCH_checked_ok_in_old_version enum indicates that the self-intersection check has been performed by a Parasolid version 5 or earlier but not since.

If the analytic_form field is not null, it will point to a HELIX_CU_FORM node, which indicates that the curve has a helical shape, as follows:

struct HELIX_CU_FORM_s

    vector                      axis_pt                 // $v

    vector                      axis_dir                // $v

    vector                      point                   // $v

    char                        hand                    // $c

    interval                    turns                   // $i

    double                      pitch                   // $f

    double                      tol                     // $f

};

typedef struct HELIX_CU_FORM_s *HELIX_CU_FORM;

The axis_pt and axis_dir fields define the axis of the helix. The hand field is ‘+’ for a right-handed and ‘-’ for a left-handed helix. A representative point on the helix is at turn position zero. The turns field gives the extent of the helix relative to the point. For instance, an interval [0 10] indicates a start position at the point and an end 10 turns along the axis. Pitch is the distance travelled along the axis in one turn. Tol is the accuracy to which the owning B-curve fits this specification.

5.2.1.5 Intersection

An intersection curve is one of the branches of a surface / surface intersection. XT represents these curves exactly; the information held in an intersection curve node is sufficient to identify the particular intersection branch involved, to identify the behaviour of the curve at its ends, and to evaluate precisely at any point in the curve. Specifically, the data is:

The two surfaces involved in the intersection.
The two ends of the intersection curve. These are referred to as the ‘limits’ of the curve. They identify the particular branch involved.
An ordered array of points along the curve. This array is referred to as the ‘chart’ of the curve. It defines the parameterisation of the curve, which increases as the array index increases.

The natural tangent to the curve at any point (i.e. in the increasing parameter direction) is given by the vector cross-product of the surface normals at that point, taking into account the senses of the surfaces.

Singular points where the cross-product of the surface normals is zero, or where one of the surfaces is degenerate, are called terminators. Intersection curves do not contain terminators in their interior. At terminators, the tangent to the curve is defined by the limit of the curve tangent as the curve parameter approaches the terminating value.

Field Name	Data Type	Description
`surface`	pointer array [2]	surfaces of intersection curve
`chart`	Pointer	array of hvecs on the curve - see below
`start`	Pointer	start limit of the curve
`end`	Pointer	end limit of the curve
intersection_data	Pointer	optional structure for storing additional information associated with an intersection curve

struct INTERSECTION_s == ANY_CURVE_s // Intersection

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  CURVE_OWNER_u          owner;               // $p

    union  CURVE_u                next;                // $p

    union  CURVE_u                previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    union  SURFACE_u             surface[ 2 ];         // $p[2]

    struct CHART_s               *chart;               // $p

    struct LIMIT_s               *start;               // $p

    struct LIMIT_s               *end;                 // $p

nolog struct INTERSECTION_DATA *intersection_data      // $p

};

typedef struct INTERSECTION_s *INTERSECTION;

A point on an intersection curve is stored in a data structure called an hvec (hepta-vec , or 7-vector ):

typedef struct hvec_s         // hepta_vec

    vector          Pvec;               //position

    double          u[2];               //surface parameters

    double          v[2];

    vector          Tangent;            //curve tangent

    double          t;                  //curve parameter

    } hvec;

Where:

pvec is a point common to both surfaces.
u[] and v[] are the u and v parameters of the pvec on each of the surfaces.
tangent is the tangent to the curve at pvec . This will be equal to the (normalized) vector cross product of the surface normals at pvec , when this cross product is non-zero. These surface normals take account of the surface sense fields.
t is the parameter of the pvec on the curve

Note: Only the


pvec

part of an


hvec

is actually transmitted.

The chart data structure essentially describes a piecewise-linear (chordal) approximation to the true curve. As well as containing the ordered array of hvec’s defining this approximation, it contains extra information pertaining to the accuracy of the approximation:

struct CHART_s          //Chart

    double              base_parameter;                // $f

    double              base_scale;                    // $f

    int                 chart_count;                   // $d

    double              chordal_error;                 // $f

    double              angular_error;                 // $f

    double              parameter_error[2];            // $f[2]

    hvec                hvec[ 1 ];                     // $h[]

};

typedef struct CHART_s *CHART;

Where:

base_parameter is the parameter of the first hvec in the chart.
base_scale determines the scale of the parameterization (see below).
chart_count is the length of the hvec array.
chordal_error is an estimate of the maximum deviation of the curve from the piecewise-linear approximation given by the hvec array. It may be null.
angular_error is the maximum angle between the tangents of two sequential hvecs . It may be null.
parameter_error[] is always [null, null].
hvec[] is the ordered array of hvec’s.

The limits of the intersection curve are stored in the following data structure:

struct LIMIT_s          // Limit

    char                type;                          // $c

char  term_use;//$c

    hvec                hvec[ 1 ];                     // $h[]

};

typdef struct LIMIT_s *LIMIT;

The ‘type’ field may take one of the following values

    const char SCH_help           =´H´;      // help hvec

    const char SCH_terminator     =´T´;      // terminator

    const char SCH_limit          =´L´;      // arbitrary limit

    const char SCH_boundary       =´B´;      // spine boundary

The ‘term_use’ field takes one of the following values

const char SCH_unset_char = ´?´ //generic uninvestigated value

const char SCH_first =´F´       //first item

const char SCH_second =´S´      //second item

The length of the hvec array depends on the type of the limit.

a SCH_help limit is an arbitrary point on a closed intersection curve. There will be one hvec in the hvec array, locating the curve.
a SCH_terminator limit is a point where one of the surface normals is degenerate, or where their cross-product is zero. Typically, there will be more than one branch of intersection between the two surfaces at these singularities. There will be two values in the hvec array. The first will be the exact position of the singularity, and the second will be a point on the curve a small distance away from the terminator. This ‘branch point’ identifies which branch relates to the curve in question. The branch point is the one which appears in the chart, at the corresponding end - so the singularity lies just outside the parameter range of the chart.
a SCH_limit limit is an artificial boundary of an intersection curve on an otherwise potentially infinite branch. The single hvec describes the end of the curve.
a SCH_boundary limit is used to describe the end of a degenerate rolling-ball blend. It is not relevant to intersection curves.

The parameterisation of the curve is given as follows. If the chart points are Pi , i = 0 to n , with parameters ti , and natural tangent vectors Ti , then define

Ci = | Pi+1 - Pi |

cos(ai) = Ti.(Pi+1 - Pi)/Ci

cos(bi) = Ti.(Pi - Pi-1)/Ci-1

Then at any chart point Pi the angles ai and bi are the deviations between the tangent at the chart point and the next and previous chords respectively.

Let f0 = base_scale

fi = (cos(bi) / cos(ai)) fi-1

Then t0 = base_parameter

ti = ti-1 + Ci-1 fi-1

The factors fi are chosen so that the parameterisation is C1 . The parameter of a point between two chart points is given by projecting the point onto the chord between the previous and next chart points.

The point on the intersection curve corresponding to a given parameter is defined as follows:

For a parameter equal to that of a chart point, it is the position of the chart point.
For a parameter interior to the chart, it is the local point of intersection of three surfaces: the two surfaces of the intersection, and a plane defined by the chart. If the parameter t lies between chart parameters ti , ti+1 , then the chord point corresponding to t lies at

(ti+1 - t) / (ti+1 - ti) Pi + (t - ti) / (ti+1 - ti) Pi+1

The plane lies through this point and is orthogonal to the chord (Pi+1, Pi ).

For a parameter between a branch chart point and a terminator, it is the local point of intersection of three surfaces: one of the intersection surfaces and two planes. Surface[0] is used unless

it is singular at the terminator and surface[1] is not
or it has the node type BLEND_BOUND_nt
or ‘term_use’ specifies to use surface[1]

The first plane contains the chord between the branch and the terminator, and the normal of the chosen intersection surface at the terminator or the curve tangent at the branch chart point if the surface normal cannot be defined. The second plane is the plane orthogonal to the chord between the branch and terminator points through the chord point as calculated above.

The intersection_data node is an optional structure for storing surface uv parameters from hvecs that are associated with an intersection curve.

Note: The


intersection_data

must match the hvecs

struct INTERSECTION_DATA_s          //Intersection data

    SCH_intersection_uv_type_t uv_type; // $u

    double values [1]; // $f[]

};

typedef struct INTERSECTION_DATA_s*INTERSECTION_DATA;

               inline double      *SCH_INTERSECTION_DATA_values(INTERSECTION_DATA self)

   return self -> values;

SCH_define_init_fn_m(INTERSECTION_DATA_s, self,

                     self -> uv_type = SCH_intersection_uv_none;

                     double*values   = SCH_INTERSECTION_DATA_values(self);

                         for (int i = 0; i< n_variable; ++i)

                         values [i] = null;

The intersection_data node contains an enum value and a variable length double array. The enum value specifies the uv values stored in the values array and is set based on the following:

typedef enum

    SCH_intersection_uv_none      = 1,

    SCH_intersection_uv_first     = 2,

    SCH_intersection_uv_second    = 3,

    SCH_intersection_uv_both      = 4,

    SCH_intersection_uv_type_t;

char *SCH_intersection_uv_type_sprintf

The uv values are converted to the number of parameters which are stored for each chart hvec as follows:

If SCH_intersection_uv_none , the number of parameters is 0
If SCH_intersection_uv_first or SCH_intersection_uv_second , the number of parameters is 2
If SCH_intersection_uv_both , the number of parameters is 4

The variable length double array contains these parameters, and the start and end limits. The values for the start and end limits can be found in the variable length arrays in the LIMIT start, and LIMIT end fields of the INTERSECTION node.

The number of values in the double array is calculated as:

(The number of chart points + The number of terminator limits) * (The number of parameters per hvec)

For each terminator present in the array the number of values will increase by 0, 2, or 4 depending on the intersection_uv_type field. For example, if both the start and the end limits are terminators and the intersection_uv_type is set to SCH_intersection_uv_both the value will increase by 8.

The order of values in the array is as follows:

If the start limit is a terminator:

If the intersection_uv_type is...	The order of values in array is...
`SCH_intersection_uv_first` or`SCH_intersection_uv_both`	intersection node ->start->hvec[0].u[0] intersection node ->start->hvec[0].v[0]
`SCH_intersection_uv_second` or `SCH_intersection_uv_both`	intersection node ->start ->hvec[0].u[1] intersection node ->start ->hvec[0].v[1]

If the intersection_uv_type is...

The order of values in array is...

SCH_intersection_uv_first orSCH_intersection_uv_both

intersection node ->start->hvec[0].u[0]

intersection node ->start->hvec[0].v[0]

SCH_intersection_uv_second or SCH_intersection_uv_both

intersection node ->start ->hvec[0].u[1]

intersection node ->start ->hvec[0].v[1]

For each hvec in the chart:

If the intersection_uv_type is...	The order of values in array is...
`SCH_intersection_uv_first` or`SCH_intersection_uv_both`	intersection node->chart ->hvec[i].u[0] intersection node->chart ->hvec[i].v[0]
`SCH_intersection_uv_second` or `SCH_intersection_uv_both`	intersection node->chart ->hvec[i].u[1] intersection node->chart ->hvec[i].v[1]

If the intersection_uv_type is...

The order of values in array is...

SCH_intersection_uv_first orSCH_intersection_uv_both

intersection node->chart ->hvec[i].u[0]

intersection node->chart ->hvec[i].v[0]

SCH_intersection_uv_second or SCH_intersection_uv_both

intersection node->chart ->hvec[i].u[1]

intersection node->chart ->hvec[i].v[1]

chart hvecs are wrapped in a loop where i = 0 to the (number of chart hvecs -1).

If end limit is a terminator:

If the intersection_uv_type is...	The order of values in array is...
`SCH_intersection_uv_first` or`SCH_intersection_uv_both`	intersection node->end ->hvec[0].u[0] intersection node->end ->hvec[0].v[0]
`SCH_intersection_uv_second` or `SCH_intersection_uv_both`	intersection node->end ->hvec[0].u[1] intersection node->end ->hvec[0].v[1]

If the intersection_uv_type is...

The order of values in array is...

SCH_intersection_uv_first orSCH_intersection_uv_both

intersection node->end ->hvec[0].u[0]

intersection node->end ->hvec[0].v[0]

SCH_intersection_uv_second or SCH_intersection_uv_both

intersection node->end ->hvec[0].u[1]

intersection node->end ->hvec[0].v[1]

5.2.1.6 Trimmed_curve

A trimmed curve is a bounded region of another curve, referred to as its basis curve. It is defined by the basis curve and two points and their corresponding parameters. Trimmed curves are most commonly attached to fins (fins) of tolerant edges in order to specify which portion of the underlying basis curve corresponds to the tolerant edge. They are necessary since the tolerant vertices of the edge do not necessarily lie exactly on the basis curve; the ‘point’ fields of the trimmed curve lie exactly on the basis curve, and within tolerance of the relevant vertex.

The rules governing the parameter fields and points are:

point_1 and point_2 correspond to parm_1 and parm_2 respectively.
If the basis curve has positive sense, parm_2 > parm_1 .
If the basis curve has negative sense, parm_2 < parm_1 .

In addition,

For open basis curves.

Both parm_1 and parm_2 shall be in the parameter range of the basis curve.
point_1 and point_2 shall not be equal.

For periodic basis curves

parm_1 shall lie in the base range of the basis curve.
If the whole basis curve is required then parm_1 and parm_2 should be a period apart and point_1 = point_2 . Equality of parm_1 and parm_2 is not permitted.
parm_1 and parm_2 shall not be more than a period apart.

For closed but non-periodic basis curves

Both parm_1 and parm_2 shall be in the parameter range of the basis curve.
If the whole of the basis curve is required, parm_1 and parm_2 shall lie close enough to each end of the valid parameter range in order that point_1 and point_2 are coincident to XT tolerance (1.0e-8 by default).

The sense of a trimmed curve is positive.

Field name	Data type	Description
`basis curve`	pointer	basis curve
`point_1`	vector	start of trimmed portion
`point_2`	vector	end of trimmed portion
`parm_1`	double	parameter on basis curve corresponding to point_1
`parm_2`	double	parameter on basis curve corresponding to point_2

struct TRIMMED_CURVE_s == ANY_CURVE_s  //Trimmed Curve

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  CURVE_OWNER_u          owner;               // $p

    union  CURVE_u                next;                // $p

    union  CURVE_u                previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    union  CURVE_u                basis_curve;         // $p

    vector                        point_1;             // $v

    vector                        point_2;             // $v

    double                        parm_1;              // $f

    double                        parm_2;              // $f

};

typedef struct TRIMMED_CURVE_s *TRIMMED_CURVE;

5.2.1.7 PE_CURVE (Foreign geometry curve)

Foreign geometry in XT is a type used for representing customers’ in-house proprietary data. It is also known as PE (parametrically evaluated) geometry. It can also be used internally for representing geometry connected with this data (for example, offsets of foreign surfaces). These two types of foreign geometry usage are referred to as ‘external’ and ‘internal’ PE data respectively. Internal PE-curves are not used at present.

Applications not using foreign geometry will never encounter either external or internal PE data structures at Parasolid V9 or beyond.

Field name	Data type	Description
`type`	char	whether internal or external
`data`	pointer	internal or external data
`tf`	pointer(0)	transform applied to geometry
`internal geom`	pointer array	reference to other related geometry

union PE_DATA_u  //PE_data_u

struct EXT_PE_DATA_s  *external;  //$p

struct INT_PE_DATA_s  *internal;  //$p

};

typedef union PE_DATA_u PE_DATA;

The PE internal geometry union defined below is used by internal foreign geometry only.

union PE_INT_GEOM_u

union SURFACE_u  surface;  //$p

union CURVE_u  curve;      //$p

};

typedef union PE_INT_GEOM_u PE_INT_GEOM;

struct PE_CURVE_s == ANY_CURVE_s  //PE_curve

int  node_id;                               /$d

union ATTRIB_FEAT_u  attributes_features;   //$p

union CURVE_OWNER_u  owner;                 //$p

union CURVE_u  next;                        //$p

union CURVE_u  previous;                    //$p

struct GEOMETRIC_OWNER_s  *geometric_owner; //$p

char  sense;                                //$c

char  type;                                 //$c

union PE_DATA_u  data;                      //$p

struct TRANSFORM_s  *tf;                    //$p

union PE_INT_GEOM_u  internal_geom[ 1 ];    //$p[]

};

typedef struct PE_CURVE_s *PE_CURVE;

The type of the foreign geometry (whether internal or external) is identified in the PE-curve node by means of the char ‘type’ field, taking one of the values:

const char SCH_external = ´E´; //external PE geometry

const char SCH_interna = ´I´; //internal PE geometry

The PE_data union is used in a PE curve or surface node to identify the internal or external evaluator corresponding to the geometry, and also holds an array of real and/or integer parameters to be passed to the evaluator. The data stored corresponds exactly to that passed to the XT routine PK_FSURF_create when the geometry is created.

struct EXT_PE_DATA_s //ext_PE_data

struct KEY_s  *key;                    //$p

struct REAL_VALUES_s  *real_array;     //$p

struct INT_VALUES_s  *int_array;       //$p

};

typedef struct EXT_PE_DATA_s *EXT_PE_DATA;

struct INT_PE_DATA_s // int_PE_data

int  geom_type;                        //$d

struct REAL_VALUES_s  *real_array;     //$p

struct INT_VALUES_s  *int_array;       //$p

};

typedef struct INT_PE_DATA_s *INT_PE_DATA;

The only internal pe type in use at the moment is the offset PE-surface, for which the geom_type is 2.

5.2.1.8 SP_CURVE

An SP-curve is the 3D curve resulting from embedding a 2D curve in the parameter space of a surface.

The 2D curve shall be a 2D B-curve; that is it shall either be a rational B-curve with a vertex dimensionality of 3, or a non-rational B-curve with a vertex dimensionality of 2.

Field name	Data type	Description
`surface`	pointer	surface
`b_curve`	pointer	2D B-curve
`original`	pointer(0)	not used
`tolerance_to_original`	double	not used

struct SP_CURVE_s == ANY_CURVE_s //SP curve

    int                           node_id;                // $d

    union  ATTRIB_FEAT_u          attributes_features;    // $p

    union  CURVE_OWNER_u          owner;                  // $p

    union  CURVE_u                next;                   // $p

    union  CURVE_u                previous;               // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;        // $p

    char                          sense;                  // $c

    union  SURFACE_u              surface;                // $p

    struct B_CURVE_s             *b_curve;                // $p

    union  CURVE_u                 original;              // $p

    double                        tolerance_to_original;  // $f

};

typedef struct SP_CURVE_s *SP_CURVE;

5.2.1.9 Polyline

A polyline describes a connected chain of linear segments. It takes the following additional field:

Field name	Data type	Description
`data`	pointer	contains the data information of the polyline.

struct POLYLINE_s == ANY_CURVE_s  //Polyline

  int                        node_id;             //$d

  union ATTRIB_FEAT_u        attributes_features; //$p

  union CURVE_OWNER_u        owner;               //$p

  union CURVE_u              next;                //$p

  union CURVE_u              previous;            //$p

  struct GEOMETRIC_OWNER_s  *geometric_owner;     //$p

  char                       sense;               //$c

  struct POLYLINE_DATA_s    *data;                //$p

};

typedef struct POLYLINE_s *POLYLINE;

The data stored in the XT data for a POLYLINE is as follows:

struct POLYLINE_DATA_s  //Polyline data

  int       n_pvecs;              //$d

  logical   closed;               //$I

  double    base_parm;            //$f

  struct    POINT_VALUES_s*pvec;  //$p

};

typedef struct POLYLINE_DATA_s*POLYLINE_DATA;

Where:

Field name	Data type	Description
`n_pvecs`	integer	number of point vectors
closed	logical	true if polyline is closed
base_parm	double	the parameter of the first pvec in the polyline
pvec	pointer	point vectors that describe the shape of the polyline

5.2.2 Surfaces

All surface nodes share the following common fields:

Field name	Data type	Description
`node_id`	int	integer value unique to surface in part
`attributes_features`	pointer0	attributes and features associated with surface
`owner`	pointer	topological owner
`next`	pointer0	next surface in geometry chain
`previous`	pointer0	previous surface in geometry chain
`geometric_owner`	pointer0	geometric owner node
`sense`	char	sense of surface: ‘+’ or ‘-’(see end of Geometry section)

struct ANY_SURF_s     //Any Surface

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

};

typedef struct ANY_SURF_s *ANY_SURF;

5.2.2.1 Plane

A plane has a parametric representation of the form

R(u, v) = P + uX + vY

Where:

P is a point on the plane

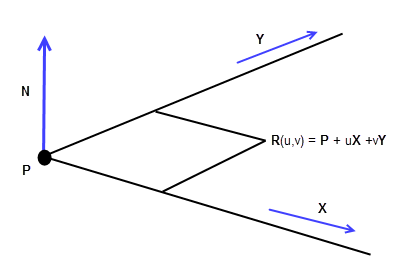
X and Y are axes in the plane

Field name	Data type	Description
`pvec`	vector	point on the plane
`normal`	vector	normal to the plane (a unit vector)
`x_axis`	vector	X axis of the plane (a unit vector)

The Y axis in the definition above is the vector cross product of the normal and x_axis .

struct PLANE_s == ANY_SURF_s      //Plane

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    vector                        pvec;                // $v

    vector                        normal;              // $v

    vector                        x_axis;              // $v

};

typedef struct PLANE_s *PLANE;

5.2.2.2 Cylinder

A cylinder has a parametric representation of the form:

R(u,v) = P + rXcos(u) + rYsin(u) + vA

Where:

P is a point on the cylinder axis.
r is the cylinder radius.
A is the cylinder axis.
X and Y are unit vectors such that A , X and Y form an orthonormal set.

Field name	Data type	Description
`pvec`	vector	point on the cylinder axis
`axis`	vector	direction of the cylinder axis (a unit vector)
`radius`	double	radius of cylinder
`x_axis`	vector	X axis of the cylinder (a unit vector)

The Y axis in the definition above is the vector cross product of the axis and x_axis .

struct CYLINDER_s == ANY_SURF_s   //Cylinder

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    vector                        pvec;                // $v

    vector                        axis;                // $v

    double                        radius;              // $f

    vector                        x_axis;              // $v

};

typedef struct CYLINDER_s *CYLINDER;

5.2.2.3 Cone

A cone in XT is only half of a mathematical cone. By convention, the cone axis points away from the half of the cone in use. A cone has a parametric representation of the form:

R(u, v) = P - vA + (Xcos(u) + Ysin(u))(r + vtan(a))

Where:

P is a point on the cone axis.
r is the cone radius at the point P.
A is the cone axis.
X and Y are unit vectors such that A , X and Y form an orthonormal set, i.e. Y = A x X .
a is the cone half angle.

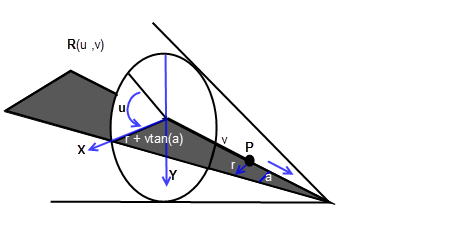
Note: At the PK interface, the cone axis is in the opposite direction to that stored in the XT data.

Field name	Data type	Description
`pvec`	vector	point on the cone axis
`axis`	vector	direction of the cone axis (a unit vector)
`radius`	double	radius of the cone at its pvec
`sin_half_angle`	double	sine of the cone’s half angle
`cos_half_angle`	double	cosine of the cone’s half angle
`x_axis`	vector	X axis of the cone (a unit vector)

The Y axis in the definition above is the vector cross product of the axis and x_axis .

struct CONE_s == ANY_SURF_s       //Cone

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    vector                        pvec;                // $v

    vector                        axis;                // $v

    double                        radius;              // $f

    double                        sin_half_angle;      // $f

    double                        cos_half_angle;      // $f

    vector                        x_axis;              // $v

};

typedef struct CONE_s *CONE;

5.2.2.4 Sphere

A sphere has a parametric representation of the form:

R(u, v) = C + (Xcos(u) + Ysin(u)) rcos(v) + rAsin(v)

Where:

C is centre of the sphere.
r is the sphere radius.

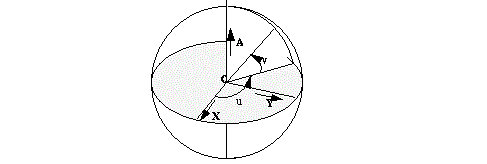
A , X and Y form an orthonormal axis set.

Field name	Data type	Description
`centre`	vector	centre of the sphere
`radius`	double	radius of the sphere
`axis`	vector	A axis of the sphere (a unit vector)
`x_axis`	vector	X axis of the sphere (a unit vector)

The Y axis of the sphere is the vector cross product of its A and X axes.

struct SPHERE_s == ANY_SURF_s     //Sphere

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    vector                        centre;              // $v

    double                        radius;              // $f

    vector                        axis;                // $v

    vector                        x_axis;              // $v

};

typedef struct SPHERE_s *SPHERE;

5.2.2.5 Torus

A torus has a parametric representation of the form

R(u, v) = C + (X cos(u) + Y sin(u))(a + b cos(v)) + b A sin(v)

Where:

C is centre of the torus.
A is the torus axis.
a is the major radius.
b is the minor radius.
X and Y are unit vectors such that A , X and Y form an orthonormal set.

In XT, there are three types of torus:

Doughnut - the torus is not self-intersecting (a > b )

Apple - the outer part of a self-intersecting torus (a <= b, a > 0 )

Lemon - the inner part of a self-intersecting torus (a < 0, |a| < b )

The limiting case a = b is allowed; it is called an ‘osculating apple’, but there is no ‘lemon’ surface corresponding to this case.

The limiting case a = 0 cannot be represented as a torus; this must be represented as a sphere.

Field name	Data type	Description
`centre`	vector	centre of the torus
`axis`	vector	axis of the torus (a unit vector)
`major_radius`	double	major radius
`minor_radius`	double	minor radius
`x_axis`	vector	X axis of the torus (a unit vector)

The Y axis in the definition above is the vector cross product of the axis of the torus and the x_axis .

struct TORUS_s == ANY_SURF_s      //Torus

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    vector                        centre;              // $v

    vector                        axis;                // $v

    double                        major_radius;        // $f

    double                        minor_radius;        // $f

    vector                        x_axis;              // $v

};

typedef struct TORUS_s *TORUS;

5.2.2.6 Blended_edge (Rolling ball blend)

XT supports exact rolling ball blends. They have a parametric representation of the form

R(u, v) = C(u) + rX(u)cos(v a(u)) + rY(u)sin(va(u))

Where:

C(u) is the spine curve
r is the blend radius
X(u) and Y(u) are unit vectors such that C’(u). X(u) = C’(u). Y(u) = 0
a(u) is the angle subtended by points on the boundary curves at the spine

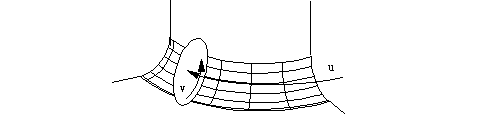
X and Y are expressed as functions of u , as their values change with u .

The spine of the rolling ball blend is the center line of the blend; i.e. the path along which the center of the ball moves.

Field name	Data type	Description
`type`	char	type of blend: ‘R’ or ‘E’
`surface`	pointer[2]	supporting surfaces (adjacent to original edge)
`spine`	pointer	spine of blend
`range`	double[2]	offsets to be applied to surfaces
`thumb_weight`	double[2]	always [1,1]
`boundary`	pointer0[2]	always [0, 0]
`start`	pointer0	Start LIMIT in certain degenerate cases
`end`	pointer0	End LIMIT in certain degenerate cases

struct BLENDED_EDGE_s == ANY_SURF_s  //Blended edge

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    char                          blend_type;          // $c

    union  SURFACE_u              surface[2];          // $p[2]

    union  CURVE_u                spine;               // $p

    double                        range[2];            // $f[2]

    double                        thumb_weight[2];     // $f[2]

    union  SURFACE_u              boundary[2];         // $p[2]

    struct LIMIT_s               *start;               // $p

    struct LIMIT_s               *end;                 // $p

};

typedef struct BLENDED_EDGE_s *BLENDED_EDGE;

The parameterisation of the blend is as follows. The u parameter is inherited from the spine, the constant u lines being circles perpendicular to the spine curve. The v parameter is zero at the blend boundary on the first surface, and one on the blend boundary on the second surface; unless the sense of the spine curve is negative, in which case it is the other way round. The v parameter is proportional to the angle around the circle.

XT data can contain blends of the following types:

    const char SCH_rolling_ball = ´R´;   // rolling ball blend

    const char SCH_cliff_edge =   ´E´;   // cliff edge blend

For rolling ball blends, the spine curve will be the intersection of the two surfaces obtained by offsetting the supporting surfaces by an amount given by the respective entry in range[] . Note that the offsets to be applied may be positive or negative, and that the sense of the surface is significant; i.e. the offset vector is the natural unit surface normal, times the range, times -1 if the sense is negative.

For cliff edge blends, one of the surfaces will be a blended_edge with a range of [0,0]; its spine will be the cliff edge curve, and its supporting surfaces will be the surfaces of the faces adjacent to the cliff edge. Its type will be R .

The limit fields will only be non-null if the spine curve is periodic but the edge curve being blended has terminators - for example if the spine is elliptical but the blend degenerates. In this case the two LIMIT nodes, of type ‘L’, determine the extent of the spine.

5.2.2.7 Blend_bound (Blend boundary surface)

A blend_bound surface is a construction surface, used to define the boundary curve where a blend becomes tangential to its supporting surface. It is an implicit surface defined internally so that it intersects one of the supporting surfaces along the boundary curve. It is orthogonal to the blend and the supporting surface along this boundary curve. The supporting surface corresponding to the blend_bound is

Blend_bound -> blend.blended_edge -> surface[1-blend_bound->boundary]

Blend boundary surfaces have no parameterisation, but are defined by the distance function

f(X) = f0 (X + r1 * grad_f1 (X)) - r0

Where:

f0 is the surface distance function of the supporting surface corresponding to the blend_bound
r0 is the blend radius corresponding to that supporting surface
f1 is the surface distance function of the other supporting surface of the blend
r1 is the blend radius corresponding to the other supporting surface

Blend boundary surfaces are most commonly referenced by the intersection curve representing the boundary curve of the blend.

The data stored in the XT data for a blend_bound is only that necessary to identify the relevant blend and supporting surface:

Field name	Data type	Description
`boundary`	short	index into supporting surface array
`blend`	pointer	corresponding blend surface

struct BLEND_BOUND_s == ANY_SURF_s  //Blend boundary

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    short                         boundary;            // $n

    union  SURFACE_u              blend;               // $p

};

typedef struct BLEND_BOUND_s *BLEND_BOUND;

The supporting surface corresponding to the blend_bound is

Blend_bound -> blend.blended_edge -> surface[1-blend_bound->boundary]

5.2.2.8 Offset_surf

An offset surface is the result of offsetting a surface a certain distance along its normal, taking into account the surface sense. It inherits the parameterisation of this underlying surface.

Field name	Data type	Description
`check`	char	check status
`true_offset`	logical	not used
`surface`	pointer	underlying surface
`offset`	double	signed offset distance
`scale`	double	for internal use only - may be set to null

struct OFFSET_SURF_s == ANY_SURF_s  //Offset surface

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    char                          check;               // $c

    logical                       true_offset;         // $l

    union  SURFACE_u              surface;             // $p

    double                        offset;              // $f

    double                        scale;               // $f

};

typedef struct OFFSET_SURF_s *OFFSET_SURF;

The offset surface is subject to the following restrictions:

The offset distance shall not be within modeller linear resolution of zero
The sense of the offset surface shall be the same as that of the underlying surface
Offset surfaces may not share a common underlying surface

The ‘check’ field may take one of the following values:

    const char SCH_valid      = ´V´;    // valid

    const char SCH_invalid    = ´I´;    // invalid

    const char SCH_unchecked  = ´U´;    // has not been checked

5.2.2.9 B_surface

XT supports B-spline surfaces in full NURBS format.

B-SURFACE DEFINITION

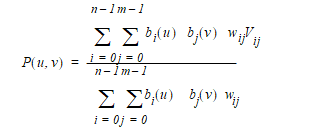
The B-surface definition is best thought of as an extension of the B-curve definition into two parameters, usually called u and v . Two knot sets are required and the number of control vertices is the product of the number that would be required for a curve using each knot vector. The rules for periodicity and closure given above for curves are extended to surfaces in an obvious way.

For attachment to topology a B-surface is required to have G1 continuity. That is to say that the surface normal direction shall be continuous.

XT does not support modelling with surfaces that are self-intersecting or contain cusps. Although they can be created they are not permitted to be attached to topology.

Field name	Data type	Description
`nurbs`	pointer	Geometric definition
`data`	pointer0	Auxiliary information

struct B_SURFACE_s == ANY_SURF_s  //B surface

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    struct NURBS_SURF_s          *nurbs;               // $p

    struct SURFACE_DATA_s        *data;                // $p

};

typedef struct B_SURFACE_s *B_SURFACE;

The data stored in the XT data for a NURBS surface is:

Field name	Data type	Description
`u_periodic`	logical	true if surface is periodic in u parameter
`v_periodic`	logical	true if surface is periodic in v parameter
`u_degree`	short	u degree of the surface
`v_degree`	short	v degree of the surface
`n_u_vertices`	int	number of control vertices (‘poles’) in u direction
`n_v_vertices`	int	number of control vertices (‘poles’) in v direction
`u_knot_type`	byte	form of u knot vector - see “B-curve”
`v_knot_type`	byte	form of v knot vector
`n_u_knots`	int	number of distinct u knots
`n_v_knots`	int	number of distinct v knots
`rational`	logical	true if surface is rational
`u_closed`	logical	true if surface is closed in u
`v_closed`	logical	true if surface is closed in v
`surface_form`	byte	shape of surface, if special
`vertex_dim`	short	dimension of control vertices
`bspline_vertices`	pointer	control vertices (poles) node
`u_knot_mult`	pointer	multiplicities of u knot vector
`v_knot_mult`	pointer	multiplicities of v knot vector
`u_knots`	pointer	u knot vector
`v_knots`	pointer	v knot vector

The surface form enum is defined below.

typedef enum

    SCH_unset              = 1,          //Unknown

    SCH_arbitrary          = 2,          //No particular shape

    SCH_planar             = 3,

    SCH_cylindrical        = 4,

    SCH_conical            = 5,

    SCH_spherical          = 6,

    SCH_toroidal           = 7,

    SCH_surf_of_revolution = 8,

    SCH_ruled              = 9,

    SCH_quadric            = 10,

    SCH_swept              = 11

    SCH_surface_form_t;

struct NURBS_SURF_s               //NURBS surface

    logical                       u_periodic;           // $l

    logical                       v_periodic;           // $l

    short                         u_degree;             // $n

    short                         v_degree;             // $n

    int                           n_u_vertices;         // $d

    int                           n_v_vertices;         // $d

    SCH_knot_type_t               u_knot_type;          // $u

    SCH_knot_type_t               v_knot_type;          // $u

    int                           n_u_knots;            // $d

    int                           n_v_knots;            // $d

    logical                       rational;             // $l

    logical                       u_closed;             // $l

    logical                       v_closed;             // $l

    SCH_surface_form_t            surface_form;         // $u

    short                         vertex_dim;           // $n

    struct BSPLINE_VERTICES_s    *bspline_vertices;     // $p

    struct KNOT_MULT_s           *u_knot_mult;          // $p

    struct KNOT_MULT_s           *v_knot_mult;          // $p

    struct KNOT_SET_s            *u_knots;              // $p

    struct KNOT_SET_s            *v_knots;              // $p

};

typedef struct NURBS_SURF_s *NURBS_SURF;

The bspline_vertices , knot_set and knot_mult nodes and the knot_type enum are described in the documentation for BCURVE.

The ‘surface data’ field in a B-surface node is a structure designed to hold auxiliary or ‘derived’ data about the surface: it is not a necessary part of the definition of the B-surface. It may be null, or the majority of its individual fields may be null. It is recommended that it only be set by Parasolid.

struct SURFACE_DATA_s         //auxiliary surface data

    interval                  original_uint;            // $i

    interval                  original_vint;            // $i

    interval                  extended_uint;            // $i

    interval                  extended_vint;            // $i

    SCH_self_int_t            self_int;                 // $u

    char                      original_u_start;         // $c

    char                      original_u_end;           // $c

    char                      original_v_start;         // $c

    char                      original_v_end;           // $c

    char                      extended_u_start;         // $c

    char                      extended_u_end;           // $c

    char                      extended_v_start;         // $c

    char                      extended_v_end;           // $c

    char                      analytic_form_type;       // $c

    char                      swept_form_type;          // $c

    char                      spun_form_type;           // $c

    char                      blend_form_type;          // $c

    void                     *analytic_form;            // $p

    void                     *swept_form;               // $p

    void                     *spun_form;                // $p

    void                     *blend_form;               // $p

};

typedef struct SURFACE_DATA_s *SURFACE_DATA;

The ‘original_’ and ‘extended_’ parameter intervals and corresponding character fields original_u_start etc. are all connected with XT’s ability to extend B-surfaces when necessary - functionality which is commonly exploited in “local operation” algorithms for example. This is done automatically without the need for user intervention.

In cases where the required extension can be performed by adding rows or columns of control points, then the nurbs data will be modified accordingly - this is referred to as an ‘explicit’ extension. In some rational B-surface cases, explicit extension is not possible - in these cases, the surface will be ‘implicitly’ extended. When a B-surface is implicitly extended, the nurbs data is not changed, but it will be treated as being larger by allowing out-of-range evaluations on the surface. Whenever an explicit or implicit extension takes place, it is reflected in the following fields:

original_u_int and original_v_int are the original valid parameter ranges for a B-surface before it was extended
extended_u_int and extended_v_int are the valid parameter ranges for a B-surface once it has been extended.

The character fields original_u_start etc. all refer to the status of the corresponding parameter boundary of the surface before or after an extension has taken place. For B-surfaces, the character can have one of the following values:

const char SCH_degenerate = ´D´;    //Degenerate edge

const char SCH_periodic   = ´P´;    //Periodic parameterization

const char SCH_bounded    = ´B´;    //Parameterization bounded

const char SCH_closed     = ´C´;    //Closed, but not periodic

The separate fields original_u_start and extended_u_start etc. are necessary because an extension may cause the corresponding parameter boundary to become degenerate.

If the surface_data node is present, then the original_u_int , original_v_int , original_u_start , original_u_end , original_v_start and original_v_end fields should be set to their appropriate values. If the surface has not been extended, the extended_u_int and extended_v_int fields should contain null, and the extended_u_start etc. Fields should contain:

const char SCH_unset_char = '?'; //generic uninvestigated value

As soon as any parameter boundary of the surface is extended, all the fields should be set, regardless of whether the corresponding boundary has been affected by the extension.

The SCH_self_int_t enum is documented in the corresponding curve_data structure under B-curve.

The swept_form_type , spun_form_type and blend_form_type characters and the corresponding pointers swept_form , spun_form and blend_form , are for future use and are not implemented in Parasolid . The character fields should be set to SCH_unset_char (‘?’) and the pointers should be set to null pointer.

If the analytic_form field is not null, it will point to a HELIX_SU_FORM node, which indicates that the surface has a helical shape. In this case the analytic_form_type field will be set to ‘H’.

struct HELIX_SU_FORM_s

    vector                  axis_pt;                     // $v

    vector                  axis_dir;                    // $v

    char                    hand;                        // $c

    interval                turns;                       // $i

    double                  pitch;                       // $f

    double                  gap;                         // $f

    double                  tol;                         // $f

};

typedef struct HELIX_SU_FORM_s *HELIX_SU_FORM;

The axis_pt and axis_dir fields define the axis of the helix. The hand field is ‘+’ for a right-handed and ‘-’ for a left-handed helix. The turns field gives the extent of the helix relative to the profile curve which was used to generate the surface. For instance, an interval [0 10] indicates a start position at the profile curve and an end 10 turns along the axis. Pitch is the distance travelled along the axis in one turn. Tol is the accuracy to which the owning bsurface fits this specification. Gap is for future expansion and will currently be zero. The v parameter increases in the direction of the axis.

5.2.2.10 Swept_surf

A swept surface has a parametric representation of the form:

R(u, v) = C(u) + vD

Where:

C(u) is the section curve.
D is the sweep direction (unit vector).
C shall not be an intersection curve, a trimmed curve, an SP-curve or a PE-curve/foreign curve. It must be analytic or a B-curve.
The swept surface inherits its u parameterisation from the section curve.

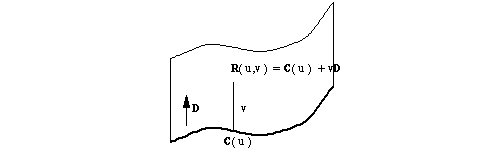
Field name	Data type	Description
`section`	pointer	section curve
`sweep`	vector	swept direction (a unit vector)
`scale`	double	for internal use only - may be set to null

struct SWEPT_SURF_s == ANY_SURF_s  //Swept surface

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    union  CURVE_u                section;             // $p

    vector                        sweep;               // $v

    double                        scale;               // $f

};

typedef struct SWEPT_SURF_s *SWEPT_SURF;

5.2.2.11 Spun_surf

A spun surface has a parametric representation of the form:

R(u, v) = Z(u) + (C(u) - Z(u))cos(v) + A X (C(u) - Z(u)) sin(v)

Where:

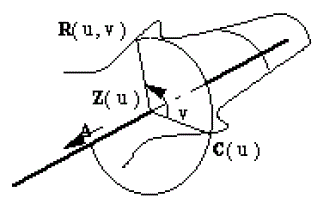
C(u) is the profile curve.
Z(u) is the projection of C(u) onto the spin axis.
A is the spin axis direction (unit vector).
C shall not be an intersection curve,a trimmed curve, an SP-curve or a PE-curve/foreign curve. It must be analytic or a B-curve.

Note:


Z(u) = P + ((C(u) - P). A)A

where P is a reference point on the axis.

Field name	Data type	Description
`profile`	pointer	profile curve
`base`	vector	point on spin axis
`axis`	vector	spin axis direction (a unit vector)
`start`	vector	position of degeneracy at low u (may be null)
`end`	vector	position of degeneracy at low v (may be null)
`start_param`	double	curve parameter at low u degeneracy (may be null)
`end_param`	double	curve parameter at high u degeneracy (may be null)
`x_axis`	vector	unit vector in profile plane if common with spin axis
`scale`	double	for internal use only - may be set to null

struct SPUN_SURF_s == ANY_SURF_s  //Spun surface

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_features; // $p

    union  SURFACE_OWNER_u        owner;               // $p

    union  SURFACE_u              next;                // $p

    union  SURFACE_u              previous;            // $p

    struct GEOMETRIC_OWNER_s     *geometric_owner;     // $p

    char                          sense;               // $c

    union  CURVE_u                profile;             // $p

    vector                        base;                // $v

    vector                        axis;                // $v

    vector                        start;               // $v

    vector                        end;                 // $v

    double                        start_param;         // $f

    double                        end_param;           // $f

    vector                        x_axis;              // $v

    double                        scale;               // $f

};

typedef struct SPUN_SURF_s *SPUN_SURF;

The ‘start’ and ‘end’ vectors correspond to physical degeneracies on the spun surface caused by the profile curve crossing the spin axis at that point. The values start_param and end_param are the corresponding parameters on the curve. These parameter values define the valid range for the u parameter of the surface. If either value is null, then the valid range for u is infinite in that direction. For example, for a straight line profile curve intersecting the spin axis at the parameter t=1 , values of null for start_param and 1 for end_param would define a cone with u parameterisation(-infinity, 1].

If the profile curve lies in a plane containing the spin axis, then x_axis shall be set to a vector perpendicular to the spin axis and in the plane of the profile, pointing from the spin axis to a point on the profile curve in the valid range. If the profile curve is not planar, or its plane does not contain the spin axis, then x_axis should be set to null.

5.2.2.12 PE_surf (Foreign geometry surface)

Foreign (or ‘PE’) geometry in XT is a type used for representing customers’ in-house proprietary data. It can also be used internally for representing geometry connected with this data (for example, offset foreign surfaces). These two types of foreign geometry usage are referred to as ‘external’ and ‘internal’ respectively. The only internal PE-surface is the offset PE-surface.

Applications not using foreign geometry will never encounter either external or internal PE data structures at Parasolid V9 or beyond.

Field name	Data type	Description
`type`	char	whether internal or external
`data`	pointer	internal or external data
`tf`	pointer0	transform applied to geometry
`internal geom`	pointer array	reference to other related geometry

struct PE_SURF_s == ANY_SURF_s  //PE_surface

int  node_id;  //$d

union ATTRIB_FEAT_u               attributes_features;   //$p

union SURFACE_OWNER_u             owner;                 //$p

union SURFACE_u                   next;                  //$p

union SURFACE_u                   previous;              //$p

struct GEOMETRIC_OWNER_s         *geometric_owner;       //$p

char                              sense;                 //$c

char                              type;                  //$c

union PE_DATA_u                   data;                  //$p

struct TRANSFORM_s                tf;                    //$p

union PE_INT_GEOM_u               internal_geom[ 1 ];    //$p[]

};

typedef struct PE_SURF_s *PE_SURF;

The PE_DATA and PE_INT_GEOM unions are defined under ‘PE-curve’.

5.2.3 Mesh Surfaces

Each MESH surface node references a PSM_MESH node containing facet data. Meshes cannot be shared by more than one face of a body.

Field name	Data type	Description
`mesh box`	box	may contain an axis-aligned box bounding the mesh
`transform`	pointer0	transform applied
`rcv_key`	pointer0	key of XMM file containing PSM mesh data. This field is not used.
`rcv_index`	int	unique integer value corresponding to the index of the PSM_MESH in the POINTER_LIS_BLOCK used as the root node in the corresponding XT mesh data file, if used
`psm_imesh`	pointer0	a pointer to the PSM_MESH node when mesh data is embedded in the XT part or partition file
`pff_imesh`	pointer0	a pointer to mesh data in the internal debug format. This is for internal use only.

struct MESH_s == ANY_SURF_s  //Mesh

int                         node_id;              //$d

union  ATTRIB_FEAT_u        attributes_features;  //$p

union  SURFACE_OWNER_u      owner;                //$p

union  SURFACE_u            next;                 //$p

union  SURFACE_u            previous;             //$p

struct GEOMETRIC_OWNER_s   *geometric_owner;      //$p

char                        sense;                //$c

box                         mesh_box;             //$b

struct TRANSFORM_s         *transform;            //$p

union  MESH_KEY_u           rcv_key;              //$p

int                         rcv_index;            //$d

struct PSM_MESH_s          *psm_imesh;            //$p

struct PFF_MESH_s          *pff_imesh;            //$p

};

typedef struct MESH_s *MESH;

The rcv_key field is not used and must always be set to null pointer.

The PSM mesh data may be embedded in the XT part or partition file, or stored in an associated XT mesh data file. The definition of the PSM mesh data is identical in both cases. When PSM mesh data is stored in an associated XT mesh data file the psm_imesh field must be set to null pointer.

5.2.3.1 PSM mesh

Mesh data is stored in a PSM_MESH node, which is referenced by the MESH node.

The mesh data is described using the following fields:

Field Name	Data Type	Description
`precision`	byte	number format used to store the mesh data
`owner`	pointer0	mesh data owner
`position_pool`	pointer	array of positions. See Section 5.2.3.2
`normal_pool`	pointer0	array of directions stored in polar coordinates. See Section 5.2.3.4
`position_indices`	pointer	array of 3N indices into the position pool, where N is the number of facets. See Section 5.2.3.3
`normal_type`	byte	form of mesh normals
`normal_indices`	pointer0	array of 3N indices into the normal pool, where N is the number of facets. See Section 5.2.3.5

typedef enum

SCH_mesh_normal_none       = 1,

SCH_mesh_normal_per_vertex = 2,

SCH_mesh_normal_per_facet  = 3

SCH_mesh_normal_type_t;

typedef enum

SCH_mesh_precision_double  = 1,

SCH_mesh_precision_single  = 2

SCH_mesh_precision_t;

struct PSM_MESH_s  //PSM Mesh

SCH_mesh_precision_t        precision;  //$u

struct MESH_s              *owner;  //$p

struct VECTOR_COMB_s       *position_pool;  //p

struct VECTOR_COMB_s       *normal_pool;  //$p

struct INTEGER_COMB_s      *position_indices;  //$p

SCH_mesh_normal_type_t      normal_type;  //$u

struct INTEGER_COMB_s      *normal_indices;  //$p

};

The owner field is reserved for future use and must be set to null pointer.

The precision field is reserved for future use and must be set to 1, i.e. double precision.

The normal_type defines whether normals are stored, and if so, whether storage is on a per-facet or per-vertex basis. See Section 5.2.3.5, “Normal indices”, for more information.

5.2.3.2 Position pool

The position pool is an indexed point cloud. The vector array is stored using “comb” nodes, each of which consists of a “spine” array containing pointers to “tooth” arrays. Each tooth array contains the vector information. All the teeth have the same length, which is a power of 2. See Section 5.2.7, “Comb nodes” for more information on the VECTOR_COMB node.

5.2.3.3 Position indices

The mesh is defined by each facet specifying 3 positions from the position pool. The indices for these positions are stored in an integer comb, similar to the vector comb. See Section 5.2.7, “Comb nodes” for more information on INTEGER_COMB nodes.

5.2.3.4 Normal pool

The normal pool is an indexed cloud of normals, i.e. unit vectors. These are stored in double-precision spherical polar coordinates.

The normal pool is optional, so need not exist at all.

5.2.3.5 Normal indices

If normals are stored with the mesh they must be stored for each vertex of each facet. The type of normal storage used by the mesh data is specified by the normal_type field.

If no normals are stored, normal indices are not needed and must be set to null pointer.
If the normals are per-facet, then the number of normal indices is the same as the number of position indices, and the normal indices and position indices are parallel arrays.
Normal storage per-vertex is not implemented.

5.2.4 Lattices

Each LATTICE node references a LATTICE_DATA node containing the lattice geometry data.

Field name	Data type	Description
`node_id`	int	integer unique within part
`attribute_feature`	pointer0	attributes and features associated with lattice
`owner`	pointer0	owner
`next`	pointer0	next lattice in geometry chain
`previous`	pointer0	previous lattice in geometry chain
`geometric_owner`	pointer0	geometric owner node
`sense`	char	sense of lattice: ‘+’ or ‘-’ (see Section 5.2.8, “Curve, surface and lattice senses”)
`data`	pointer0	lattice geometry data

struct LATTICE_s                    //Lattice

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u          attributes_feature;  // $p

    union  LATTICE_OWNER_u        owner;               // $p

    struct LATTICE_s             *next;                // $p

    struct LATTICE_s             *previous;            // $p

    struct GEOMETRIC_OWNER_S     *geometric_owner;     // $p

    char                          sense;               // $c

    union  LATTICE_DATA_u         data;                // $p

};

typedef struct LATTICE_s *LATTICE

union LATTICE_OWNER_u

    struct BODY_s                *body;

    struct ASSEMBLY_s            *assembly;

    struct WORLD_s               *world;

};

typedef union LATTICE_OWNER_u LATTICE_OWNER;

union LATTICE_DATA_u

    DS_block_p_t                     any;

    struct LATTICE_DATA_IRREGULAR_s *irregular;

};

typedef union LATTICE_DATA_u LATTICE_DATA;

5.2.4.1 Irregular lattice node

Lattice data is stored in a LATTICE_DATA_IRREGULAR node, which is referenced by the LATTICE node. The lattice data is described using the following fields:

Field name	Data type	Description
`connectivity`	pointer	graph of lattice. See the GRAPH_COMPACT node below for more information.
`positions`	pointer	array of positions
`ball_type`	byte	form of ball radii
`ball_radius`	double	constant radius for balls
`ball_radii`	pointer	array of variable radii for balls
`ball_rod_radii`	pointer	array of variable radii for rods at balls
`ball_blend_type`	byte	type of blend for the balls
`ball_blend_size`	double	constant blend size for balls
`ball_blend_sizes`	pointer	array of variable blend sizes for balls if `ball_blend_type` is anything other than `SCH_ball_blend_none` and `ball_blend_size` is zero.
`rod_term_type`	byte	form of rod terminal radii
`rod_term_radius`	double	constant terminal radius for rods
rod_start_radii	pointer	array of variable radii for start of rod
rod_end_radii	pointer	array of variable radii for ends of rod
rod_mid_type	byte	form of mid radius of rods
rod_mid_radius	double	constant mid radius for rods
rod_mid_radii	pointer	array of mid radii for rods

struct LATTICE_DATA_IRREGULAR_s            //General lattice data

    struct GRAPH_COMPACT_s        *connectivity;       // $p

    struct VECTOR_COMB_s_         *positions;          // $p

    SCH_lattice_ball_type_t        ball_type;          // $u

    double                         ball_radius;        // $f

    struct REAL_COMB_s            *ball_radii;         // $p

    struct REAL_COMB_s            *ball_rod_radii;     // $p

     SCH_lattice_ball_blend_type_t  ball_blend_type;    // $u

    double                         ball_blend_size;    // $f

    struct REAL_COMB_s            *ball_blend_sizes;   // $p

    SCH_lattice_rod_term_type_t    rod_term_type;      // $u

    double                         rod_term_radius;    // $f

    struct REAL_COMB_s            *rod_start_radii;    // $p

    struct REAL_COMB_s            *rod_end_radii;      // $p

    SCH_lattice_rod_mid_type_t     rod_mid_type;       // $u

    double                         rod_mid_radius;     // $f

    struct REAL_COMB_s            *rod_mid_radii;      // $p

};

typedef struct LATTICE_DATA_IRREGULAR_s *LATTICE_DATA_IRREGULAR;

The GRAPH_COMPACT node stores graph data for a lattice and is defined as follows:

typedef struct GRAPH_COMPACT_s  //Graph data

    struct INTEGER_COMB_s       *adjacency_indices;        // $p

    struct INTEGER_COMB_s_      *adjacencies;              // $p

};

typedef struct GRAPH_COMPACT_s *GRAPH_COMPACT;

SCH_define_init_fn_m( GRAPH_COMPACT_S, SELF,

                      self -> adjacency_indices = null;

                      self -> adjacencies       = null;

The ball_type enum defines the type of ball radii

typedef short short enum

    SCH_ball_unset    = 0,

    SCH_ball_const    = 1,

    SCH_ball_variable = 2

    SCH_lattice_ball_type_t;

The ball_blend_type enum defines the type of ball blend

typedef short short enum

    SCH_ball_blend_none = 0,

    SCH_ball_blend_absolute = 1,

    SCH_ball_blend_relative = 2,

    SCH_lattice_ball_blend_type_t;

Therod_term_type enum defines the type of rod terminal radii

typedef short short enum

    SCH_rod_term_unset      = 0,

    SCH_rod_term_const      = 1,

    SCH_rod_term_derived    = 2,

    SCH_rod_term_variable_1 = 3,

    SCH_rod_term_variable_2 = 4

    SCH_lattice_rod_term_type_t;

The rod_mid_type enum defines the type of the rod mid radii

typedef short short enum

    SCH_rod_mid_unset      = 0,

    SCH_rod_mid_none       = 1,

    SCH_rod_mid_const      = 2,

    SCH_rod_mid_variable   = 3

    SCH_lattice_rod_mid_type_t;

The arrays in the LATTICE_DATA_IRREGULAR node are stored using “comb” nodes, each of which consists of a “spine” array containing pointers to “tooth” arrays. Each tooth array contains the vector or real information. See Section 5.2.7, “Comb nodes” for more information.

5.2.5 Point

Field name	Data type	Description
`node_id`	int	integer unique within part
`attributes_features`	pointer0	attributes and features associated with point
`owner`	pointer	owner
`next`	pointer0	next point in chain
`previous`	pointer0	previous point in chain
`pvec`	vector	position of point

union POINT_OWNER_u

    struct VERTEX_s              *vertex;

    struct BODY_s                *body;

    struct ASSEMBLY_s            *assembly;

    struct WORLD_s               *world;

};

struct POINT_s                    //Point

    int                           node_id;             // $d

    union  ATTRIB_FEAT_u

    attributes_features;                               // $p

    union  POINT_OWNER_u          owner;               // $p

    struct POINT_s               *next;                // $p

    struct POINT_s               *previous;            // $p

    vector                        pvec;                // $v

};

typedef struct POINT_s *POINT;

5.2.6 Transform

Field name	Data type	Description
`node_id`	int	integer unique within part
`owner`	pointer	owning instance or world
`next`	pointer0	next transform in chain
`previous`	pointer0	previous pointer in chain
`rotation_matrix`	double[3][3]	rotation component
`translation_vector`	vector	translation component
`scale`	double	scaling factor
`flag`	byte	binary flags indicating non-trivial components
`perspective_vector`	vector	perspective vector (always null vector)
precision	pointer0	additional precision data for the transform

The transform acts as:

x’ = (rotation_matrix . x + translation_vector) * scale

The ‘flag’ field contains various bit flags which identify the components of the transformation:

Field name	Data type	Description
`translation`	00001	set if translation vector non-zero
`rotation`	00010	set if rotation matrix is not the identity
`scaling`	00100	set if scaling component is not 1.0
`reflection`	01000	set if determinant of rotation matrix is negative
`general affine`	10000	set if the rotation_matrix is not a rigid rotation

union TRANSFORM_OWNER_u{

    struct INSTANCE_s          *instance;

    struct WORLD_s             *world;

};

struct TRANSFORM_s               //Transformation

    int                           node_id;                 // $d

    union TRANSFORM_OWNER_u       owner;                   // $p

    struct TRANSFORM_s           *next;                    // $p

    struct TRANSFORM_s           *previous;                // $p

    double                        rotation_matrix[3][3];   // $f[9]

    vector                        translation_vector;      // $v

    double                        scale;                   // $f

    unsigned                      flag;                    // $d

    vector                        perspective_vector;      // $v

struct TRANSFORM_PRECISION_s     *precision;               // $p

};

typedef struct TRANSFORM_s *TRANSFORM;

The TRANSFORM_PRECISION node is an optional structure for storing additional precision information of the transform and is defined as follows:

struct TRANSFORM_PRECISION_s     //Transformation precision

double  rotation_matrix[3][3];    //$f[3*3]

vector  translation_vector;       //$v

};

typedef struct TRANSFORM_PRECISION_s *TRANSFORM_PRECISION;

Note: When consuming Parasolid-native XT, the values in the TRANSFORM_PRECISION structure (when not NULL) should be added to those in the


rotation_matrix

and


translation_vector

values in the parent TRANSFORM structure.

When using the format reference to write XT data, the TRANSFORM_PRECISION structure should not typically be used.

5.2.7 Comb nodes

5.2.7.1 VECTOR_COMB nodes

The VECTOR_COMB node stores an array of double precision vectors.

The vector array is stored using “comb” nodes, each of which consists of a “spine” array containing pointers to “tooth” arrays. Each tooth array contains the vector information. All the teeth have the same length, which is a power of 2.

Field Name	Data Type	Description
`encoding`	byte	Form of the vector coordinates
`n_vectors`	int	Number of vectors stored in the comb
`n_max_vectors`	int	Maximum number of vectors for which space has been allocated in the comb
`shift`	int	Capacity of the tooth, defined as 2`shift`
`teeth`	pointer array	Array of pointers to vector teeth

struct VECTOR_TOOTH_s                         //Vector Tooth

double                      values[1];        //$f[]

};

typedef enum

SCH_vector_simple    = 1,

SCH_vector_spherical = 2

SCH_vector_encoding_t;

struct VECTOR_COMB_s  //Vector Comb

SCH_vector_encoding_t       encoding;        //$u

int                         n_vectors;       //$d

int                         n_max_vectors;   //$d

int                         shift;           //$d

struct VECTOR_TOOTH_s      *teeth[1]     ;  //$p[]

};

The encoding enum determines the number of values used to store the vectors:

simple vectors are stored as triplets of doubles corresponding to Cartesian coordinates;
spherical vectors are stored as pairs of doubles corresponding to (theta, phi) spherical coordinates. This encoding is only used for unit vectors.

5.2.7.2 INTEGER_COMB nodes

Similar to vector comb nodes and is defined as follows:

struct INTEGER_TOOTH_s                            //Integer Tooth

int                         values[1];            //$d[]

};

typedef enum

SCH_no_encoding       = 1

SCH_comb_encoding_t;

struct INTEGER_COMB_s                            //Integer Comb

SCH_comb_encoding_t         encoding;            //$u

int                         n_integers;          //$d

int                         n_max_integers;      //$d

int                         n_bits_per_integer;  //$d

int                         shift;               //$d

struct INTEGER_TOOTH_s     *teeth[1];            //$p[]

};

The encoding enum is reserved for future use. The n_bits_per_integer integer is not used and must be set to 32.

5.2.7.3 REAL_COMB nodes

These are similar to vector nodes and are described as follows:

Field Name	Data Type	Description
`encoding`	byte	Reserved for future use
`length`	int	Number of reals stored in the comb
`max_length`	int	Maximum length
`shift`	int	Capacity of the tooth, defined as 2`shift`
`teeth`	pointer array	Array of pointers to real teeth

struct REAL_TOOTH_s                            //Real Tooth

int                      values[1];            //$d[]

};

typedef enum

SCH_no_encoding       = 1

SCH_comb_encoding_t;

struct REAL_COMB_s                              //Real Comb

    SCH_comb_encoding_t         encoding;       //$u

    int                         length;         //$d

    int                         max_length;     //$d

    int                         shift;          //$d

    struct REAL_TOOTH_s        *teeth[1];       //$p[]

};

typedef struct REAL_COMB_s *REAL_COMB;

5.2.8 Curve, surface and lattice senses

The ‘natural’ tangent to a curve is that in the increasing parameter direction, and the ‘natural’ normal to a surface is in the direction of the cross-product of dP/du and dP/dv. For some purposes these are modified by the curve and surfaces senses, respectively - for example in the definition of blend surfaces, offset surfaces and intersection curves.

At the XT interface, the edge/curve and face/surface sense orientations are regarded as properties of the topology/geometry combination. In the XT format, this orientation information resides in the curves, surfaces and faces as follows:

The edge/curve orientation is stored in the curve->sense field. The face/surface orientation is a combination of sense flags stored in the face->sense and surface->sense fields, so the face/surface orientation is true (i.e. the face normal is parallel to the natural surface normal) if neither, or both, of the face and surface senses are positive.

In the XT Format, the orientation information of lattices is stored in the sense field. If the sense is positive, the interior of the lattice is considered solid, and void if the sense is negative.

5.2.9 Geometric_owner

Where geometry has dependants, the dependants point back to the referencing geometry by means of Geometric Owner nodes. Each geometric node points to a doubly-linked ring of Geometric Owner nodes which identify its referencing geometry. Referenced geometry is as follows:

Intersection: 2 surfaces.
SP-curve: Surface.
Trimmed curve: basis curve.
Blended edge: 2 supporting surfaces, 2 blend_bound surfaces, 1 spine curve.
Blend bound: blend surface.
Offset surface: underlying surface.
Swept surface: section curve.
Spun surface: profile curve.

Note: The 2D B-curve referenced by an SP-curve is not a dependent in this sense, and does not need a geometric owner node.

Field name	Data type	Description
`owner`	pointer	referencing geometry
`next`	pointer	next in ring of geometric owners referring to the same geometry
`previous`	pointer	previous in above ring
`shared_geometry`	pointer	referenced (dependent) geometry

struct GEOMETRIC_OWNER_s      //geometric owner of geometry

    union  GEOMETRY_u              owner;               // $p

    struct GEOMETRIC_OWNER_s      *next;                // $p

    struct GEOMETRIC_OWNER_s      *previous;            // $p

    union  GEOMETRY_u              shared_geometry;     // $p

};

typedef struct GEOMETRIC_OWNER_s *GEOMETRIC_OWNER;

[back to top]

5.3 Topology

In the following tables, ‘ignore’ means this may be set to null (zero) if the XT data is created outside of the Parasolid Kernel. For XT data created by the Parasolid Kernel, this may take any value, but should be ignored.

Unless otherwise stated, all chains of nodes are doubly-linked and null-terminated.

5.3.1 World

Field name	Data type	Description
`assembly`	pointer0	Head of chain of assemblies
`attribute`	pointer0	Ignore
`body`	pointer0	Head of chain of bodies. This chain contains standard and compound bodies but does not contain any child bodies.
`transform`	pointer0	Head of chain of transforms
`lattice`	pointer0	Head of chain of lattices
`surface`	pointer0	Head of chain of surfaces
`curve`	pointer0	Head of chain of curves
`point`	pointer0	Head of chain of points
`mesh`	pointer0	Head of chain of meshes
`polyline`	pointer0	Head of chain of polylines
`alive`	logical	True unless partition is at initial pmark
`attrib_def`	pointer0	Head of chain of attribute definitions
`attdef_list`	pointer0	Shallbe set to null
`highest_id`	int	Highest pmark id in partition
`current_id`	int	Id of current pmark
`index_map_offset`	int	Shallbe set to 0
`index_map`	pointer0	Shall be set to null
`schema_embedding_map`	pointer0	Shallbe set to null
`mesh_offset_data`	pointer0	Data for embedded meshes. If the XT file does not contain embedded meshes, this field must be set to null.

The World node is only used when a partition is transmitted. Because some of the attribute definitions may be referenced by nodes which have been deleted, but which may reappear on rollback, the attribute definitions are chained off the World node rather than simply being referenced by attributes.

The attdef_list field is not used and shall be set to null pointer.

The fields index_map_offset , index_map , and schema_embedding_map are used for Indexed Transmit; applications writing XT data shall set them to 0 and null.

The mesh_offset_data field is used for embedded mesh data.

struct WORLD_s                    //World

    struct ASSEMBLY_s            *assembly;              // $p

    struct ATTRIBUTE_s           *attribute;             // $p

    struct BODY_s                *body;                  // $p

    struct TRANSFORM_s           *transform;             // $p

    struct LATTICE_s             *lattice;               // $p

    union  SURFACE_u              surface;               // $p

    union  CURVE_u                curve;                 // $p

    struct POINT_s               *point;                 // $p

    union SURFACE_u               mesh;                  // $p

    union CURVE_u                 polyline;              // $p

    logical                       alive;                 // $l

    struct  ATTRIB_DEF_s         *attrib_def;            // $p

    struct  POINTER_LIS_BLOCK_s  *attdef_list;           // $p

    int                           highest_id;            // $d

    int                           current_id;            // $d

    int                           index_map_offset:      // $d

    struct INT_VALUES_s           *index_map;            // $p

    struct INT_VALUES_s           *schema_embedding_map; // $p

    struct MESH_OFFSET_DATA_s     *mesh_offset_data;     // $p

};

typedef struct WORLD_s *WORLD;

5.3.2 Assembly

Field name	Data type	Description
`highest_node_id`	int	Highest identifier in assembly
`attributes_features`	pointer0	Head of chain of attributes of/and features in assembly
`attribute_chains`	pointer0	List of attributes, one for each attribute definition used in the assembly
`list`	pointer0	Null
`lattice`	pointer0	Head of construction lattice chain
`surface`	pointer0	Head of construction surface chain
`curve`	pointer0	Head of construction curve chain
`point`	pointer0	Head of construction point chain
`mesh`	pointer0	Head of construction mesh chain
`polyline`	pointer0	Head of construction polyline chain
`key`	pointer0	Ignore
`res_size`	double	Value of ‘size box’ when transmitted (normally 1000)
`res_linear`	double	Value of linear resolution when transmitted (normally 1.0e-8). For more information on linear resolution, see Section 4.2, “General points”.
`ref_instance`	pointer0	Head of chain of instances referencing this assembly
`next`	pointer0	Ignore
`previous`	pointer0	Ignore
`state`	byte	Set to 1
`owner`	pointer0	Ignore
`type`	byte	Always 1
`sub_instance`	pointer0	Head of chain of instances in assembly
`mesh_offset_data`	pointer0	Data for embedded meshes. If the XT file does not contain embedded meshes, this field must be set to null.

The value of the ‘state’ field should be ignored, as should any nodes of type ‘KEY’ referenced by the assembly. If XT data is constructed without the use of the Parasolid Kernel, the state field should be set to 1, and the key to null.

The highest_node_id gives the highest identifier of any node in the assembly. Certain nodes within the assembly (namely instances, transforms, geometry, attributes and groups) have unique identifiers which are non-zero integers.

The mesh_offset_data field is used for embedded mesh data.

typedef enum

    SCH_collective_assembly  = 1,

    SCH_conjunctive_assembly = 2,

    SCH_disjunctive_assembly = 3

    SCH_assembly_type;

typedef enum

    SCH_new_part       = 1,

    SCH_stored_part    = 2,

    SCH_modified_part  = 3,

    SCH_anonymous_part = 4,

    SCH_unloaded_part  = 5

    SCH_part_state;

struct ASSEMBLY_s                 //Assembly

    int                           highest_node_id;      // $d

    union ATTRIB_FEAT_u           attributes_features;  // $p

    struct LIST_s                *attribute_chains;     // $p

    struct LIST_s                *list;                 // $p

    union LATTICE_u               lattice;              // $p

    union SURFACE_u               surface;              // $p

    union CURVE_u                 curve;                // $p

    struct POINT_s               *point;                // $p

    union SURFACE_u               mesh;                 // $p

    union CURVE_u                 polyline;             // $p

    struct KEY_s                 *key;                  // $p

    double                        res_size;             // $f

    double                        res_linear;           // $f

    struct INSTANCE_s            *ref_instance;         // $p

    struct ASSEMBLY_s            *next;                 // $p

    struct ASSEMBLY_s            *previous;             // $p

    SCH_part_state                state;                // $u

    struct WORLD_s               *owner;                // $p

    SCH_assembly_type             type;                 // $u

    struct INSTANCE_s            *sub_instance;         // $p

struct MESH_OFFSET_DATA_s  *mesh_offset_data;  //$p

};

typedef struct ASSEMBLY_s *ASSEMBLY;

struct KEY_s                      //Key

    string[1];                    char                  // $c[]

};

typedef struct KEY_s  *KEY;

5.3.3 Instance

Field name	Data type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of instance and `member_of_feature` instance
`type`	byte	Always 1
`part`	pointer	Part referenced by instance
`transform`	pointer0	Transform of instance
`assembly`	pointer	Assembly in which instance lies
`next_in_part`	pointer0	Next instance in assembly
`prev_in_part`	pointer0	Previous instance in assembly
`next_of_part`	pointer0	Next instance of instance->part
`prev_of_part`	pointer0	Previous instance of instance->part

Note: Only standard bodies can be instanced. Compound or child bodies cannot be instanced.

typedef enum

    SCH_positive_instance = 1,

    SCH_negative_instance = 2

    SCH_instance_type;

union  PART_u

    struct BODY_s          *body;

    struct ASSEMBLY_s      *assembly;

};

typedef union PART_u PART;

struct INSTANCE_s                 //Instance

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    SCH_instance_type             type;                  // $u

    union  PART_u                 part;                  // $p

    struct TRANSFORM_s           *transform;             // $p

    struct ASSEMBLY_s            *assembly;              // $p

    struct INSTANCE_s            *next_in_part;          // $p

    struct INSTANCE_s            *prev_in_part;          // $p

    struct INSTANCE_s            *next_of_part;          // $p

    struct INSTANCE_s            *prev_of_part;          // $p

};

typedef struct INSTANCE_s *INSTANCE;

5.3.4 Body

Field name	Data type	Description
`highest_node_id`	int	Highest identifier in a standard body. For compound bodies, this is the highest identifier, including entities in child bodies. For child bodies, this is the identifier of the child body itself. It is also the highest unique identifier of the entities which were in the child body when it was added to its parent compound body.
`attributes_features`	pointer0	Head of chain of attributes of and features in body. All features in a compound body and its children are chained off this regardless of their contents.
`attribute_chains`	pointer0	List of attributes, one for each attribute definition used in the body. For compound bodies, all attributes within the compound body and its children appear in the `attribute_chains` list for the compound body, except those attributes that are directly attached to the child bodies. These attributes appear in the `attribute_chains` list of their relevant child body.
lattice	pointer0	Head of construction lattice chain.
`surface`	pointer0	Head of construction surface chain. For a child body, these fields are always null.
`curve`	pointer0	Head of construction curve chain. For a child body, these fields are always null.
`point`	pointer0	Head of construction point chain. For a child body, these fields are always null.
`mesh`	pointer0	Head of construction mesh chain. For a child body, these fields are always null
`polyline`	pointer0	Head of construction polyline chain. For a child body, these fields are always null
`key`	pointer0	Ignore
`res_size`	double	Value of ‘size box’ when transmitted (normally 1000)
`res_linear`	double	Value of linear resolution when transmitted (normally 1.0e-8). For more information on linear resolution, see Section 4.2, “General points”.
`ref_instance`	pointer0	Head of chain of instances referencing this assembly
`next`	pointer0	For a child body, this field chains children of the same parent together.
`previous`	pointer0	For a child body, this field chains children of the same parent together.
`state`	byte	Set to 1 (see below)
`owner`	pointer0	For a child, this field references its parent compound body.
`body_type`	byte	Body type. If children of a compound body have the same `body_type` , then this will also be the `body_type` of the compound body. Otherwise, the `body_type` of the compound will be general.
`nom_geom_state`	byte	Set to 1 (for future use)
`shell`	pointer0	For general bodies: null. For solid bodies: the first shell in one of the solid regions. For other bodies: the first shell in one of the regions.This field is obsolete, and should be ignored by applications reading XT data. When writing XT data, it shall be set as above.
`boundary_surface`	pointer0	Head of chain of surfaces attached directly or indirectly to faces or edges or fins. For a child body, these fields are always null
`boundary_curve`	pointer0	Head of chain of curves attached directly or indirectly to edges or faces or fins. For a child body, these fields are always null
`boundary_point`	pointer0	Head of chain of points attached to vertices. For a child body, these fields are always null
`boundary_mesh`	pointer0	Head of chain of meshes attached directly or indirectly to faces or edges or fins. For a child body, these fields are always null
`boundary_polyline`	pointer0	Head of chain of polylines attached directly or indirectly to edges or faces or fins. For a child body, these fields are always null
`region`	pointer0	Head of chain of regions in body; this is the infinite region. For a compound body, this is the head of chain of regions comprising of all the regions of all the child bodies. The regions of each child body are contiguous in this chain and the order of the regions corresponds to the order of the children. For a child body, this field points to the first region of the child. For an empty compound body (i.e. one without any children), this field is null.
`edge`	pointer0	Head of chain of all non-wireframe edges in body. For a compound body, this is the head of a chain of all non-wireframe edges in all the children.For a child body, this field is null.
`vertex`	pointer0	Head of chain of all vertices in body. For a compound body, this is the head of a chain of all vertices in all the children.For a child body, this field is null.
`index_map_offset`	int	Shallbe set to 0
`index_map`	pointer0	Shall be set to null
`node_id_index_map`	pointer0	Shallbe set to null
`schema_embedding_map`	pointer0	Shallbe set to null
`child`	pointer0	For a compound body, this is the first child body. the children are chained using the `next` and `previous` pointers. For a standard or child body, this is null.
`lowest_node_id`	int	For a standard or compound body, this field is zero. For a child body, this is the lowest node id of the entities in the child body.
`mesh_offset_data`	pointer0	Data for embedded meshes. If the XT file does not contain embedded meshes, this field must be set to null.

The value of the ‘state’ field should be ignored, as should any nodes of type ‘KEY’ referenced by the body. If XT data is constructed without using the Parasolid Kernel, the state field should be set to 1, and the key to null.

The highest_node_id gives the highest identifier of any node in this body. Most nodes in a body which are visible at the PK interface have identifier, which are non-zero integers unique to that node within the body. Applications writing XT data shall ensure that identifiers are present and distinct. The details of which nodes have node ids are given in an appendix.

The fields index_map_offset , index_map, node_id_index_map , and schema_embedding_map are used for Indexed Transmit; applications writing XT data shall ensure that these fields are set to 0 and null.

The mesh_offset_data field is used for embedded mesh data.

typedef enum

    SCH_solid_body     = 1,

    SCH_wire_body      = 2,

    SCH_sheet_body     = 3,

    SCH_general_body   = 6

    SCH_body_type;

typedef short short enum

    SCH_nom_geom_off = 1,              --- Entirely off

    SCH_nom_geom_on  = 2,              --- Entirely on

    SCH_nom_geom_state_t;

struct BODY_s                     //Body

    int                           highest_node_id;       // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    struct LIST_s                *attribute_chains;      // $p

    union  LATTICE_u             *lattice;               // $p

    union  SURFACE_u              surface;               // $p

    union  CURVE_u                curve;                 // $p

    struct POINT_s               *point;                 // $p

    union SURFACE_u               mesh;                  // $p

    union CURVE_u                 polyline;              // $p

    struct KEY_s                 *key;                   // $p

    double                        res_size;              // $f

    double                        res_linear;            // $f

    struct INSTANCE_s            *ref_instance;          // $p

    struct BODY_s                *next;                  // $p

    struct BODY_s                *previous;              // $p

    SCH_part_state                state;                 // $u

    union BODY_OWNER_u            owner;                 // $p

    SCH_body_type                 body_type;             // $u

    SCH_nom_geom_state_t          nom_geom_state;        // $u

    struct SHELL_s               *shell;                 // $p

    union  SURFACE_u              boundary_surface;      // $p

    union  CURVE_u                boundary_curve;        // $p

    struct POINT_s               *boundary_point;        // $p

    union SURFACE_u               boundary_mesh;         // $p

    union CURVE_u                 boundary_polyline;     // $p

    struct REGION_s              *region;                // $p

    struct EDGE_s                *edge;                  // $p

    struct VERTEX_s              *vertex;                // $p

    int                           index_map_offset;      // $d

    struct INT_VALUES_s          *index_map;             // $p

    struct INT_VALUES_s          *node_id_index_map;     // $p

    struct INT_VALUES_s          *schema_embedding_map;  // $p

struct BODY_s   *child;  //$p

int   lowest_node_id;  //$d

struct MESH_OFFSET_data_s  *mesh_offset_data;  //$p

};

typedef struct BODY_s *BODY;

union BODY_OWNER_u

struct WORLD_s  *world;

struct BODY_s  *body;

};

5.3.4.1 Attaching geometry to topology

The faces which reference a surface are chained together, surface->owner is the head of this chain. Similarly the edges which reference the same curve are chained together. Fins do not share curves.

Geometry in parts may be chained into one of the three boundary geometry chains, or one of the three construction geometry chains. A geometric node will fall into one of the following cases:

Geometry	Owner	Whether chained
Attached to face	face	In boundary_surface chain
Attached to edge or fin	pointer0	In boundary_curve chain
Attached to vertex	pointer	In boundary_point chain
Indirectly attached to face or edge or fin	pointer0	In boundary_surface chain or boundary_curve chain
Construction geometry	pointer0	In lattice, surface, curve or point chain
2D B-curve in SP-curve	pointer0	Not chained
type	char	Region type - solid (‘S’) or void (‘V’)

Here ‘indirectly attached’ means geometry which is a dependent of a dependent of (... etc) of geometry attached to an edge, face or fin.

Geometry in a construction chain may reference geometry in a boundary chain, but not vice-versa.

5.3.5 Region

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of region and member of features of region
`body`	pointer	Body of region. For a region in a child body, this field references the parent compound body.
`next`	pointer0	Next region in body
`prev`	pointer0	Previous region in body
`shell`	pointer0	Head of singly-linked chain of shells in region
`type`	char	Region type - solid (‘S’) or void (‘V’)
`owner`	pointer0	For a region in a child body, this field references the child body. Otherwise, the field is null.

struct REGION_s                   //Region

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    struct BODY_s                *body;                  // $p

    struct REGION_s              *next;                  // $p

    struct REGION_s              *previous;              // $p

    struct SHELL_s               *shell;                 // $p

    char                          type;                  // $c

struct BODY_s  *owner:  //$p

};

typedef struct REGION_s *REGION;

5.3.6 Shell

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of shell
`body`	pointer0	For standard bodies: For shells in wire and sheet bodies, and for shells bounding a solid region of a solid body, this is set to the body of the shell. For shells in general bodies, or void shells in solid bodies, it is null. For shells in child bodies, this field is set to the parent compound body if the child has type wire or sheet, or if it has type solid and the shell belongs to a solid region. Otherwise, this field is null. This field is obsolete, and should be ignored by applications reading XT data. When writing XT data, it shall be set as above.
`next`	pointer0	Next shell in region
`face`	pointer0	Head of chain of back-faces of shell (i.e. faces with face normal pointing out of region of shell).
`edge`	pointer0	Head of chain of wire-frame edges of shell.
`vertex`	pointer0	If shell consists of a single vertex, this is it; else null
`region`	pointer	Region of shell
`front_face`	pointer0	Head of chain of front-faces of shell (i.e. faces with face normal pointing into region of shell).

struct SHELL_s                    //Shell

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    struct BODY_s                *body;                  // $p

    struct SHELL_s               *next;                  // $p

    struct FACE_s                *face;                  // $p

    struct EDGE_s                *edge;                  // $p

    struct VERTEX_s              *vertex;                // $p

    struct REGION_s              *region;                // $p

    struct FACE_s                *front_face;            // $p

};

typedef struct SHELL_s *SHELL;

5.3.7 Face

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of face and `member_of_` feature of face.
`tolerance`	double	Not used (null double)
`next`	pointer0	Next back-face in shell
`previous`	pointer0	Previous back-face in shell
`loop`	pointer0	Head of singly-linked chain of loops
`shell`	pointer	Shell of which this is a back-face
`surface`	pointer0	Surface of face
`sense`	char	Face sense - positive (‘+’) or negative (‘-’)
`next_on_surface`	pointer0	Next in chain of faces sharing the surface of this face
`previous_on_surface`	pointer0	Previous in chain of faces sharing the surface of this face
`next_front`	pointer0	Next front-face in shell
`previous_front`	pointer0	Previous front-face in shell
`front_shell`	pointer	Shell of which this is a front-face

struct FACE_s                     //Face

    int                           node_id;               // $d

    union ATTRIB_FEAT_u          attributes_features;   // $

    double                        tolerance;             // $f

    struct FACE_s                *next;                  // $p

    struct FACE_s                *previous;              // $p

    struct LOOP_s                *loop;                  // $p

    struct SHELL_s               *shell;                 // $p

    union  SURFACE_u              surface;               // $p

    char                          sense;                 // $c

    struct FACE_s                *next_on_surface;       // $p

    struct FACE_s                *previous_on_surface;   // $p

    struct FACE_s                *next_front;            // $p

    struct FACE_s                *previous_front;        // $p

    struct SHELL_s               *front_shell;           // $p

};

typedef struct FACE_s *FACE;

5.3.8 Loop

Field name	Type	Description
`node_id`	int	Identifier
attributes_features	pointer0	Head of chain of attributes of loop
`halfedge`	pointer	One of ring of fins of loop
`face`	pointer	Face of loop
`next`	pointer0	Next loop in face

5.3.8.1 Isolated loops

An isolated loop (one consisting of a single vertex) does not refer directly to a vertex, but points to a fin which refers to that vertex. This isolated fin has halfedge->forward = halfedge->backward = halfedge , and halfedge->other = halfedge->curve = halfedge->edge = null . Its sense is not significant. The fin is chained into the chain of fins referencing the isolated vertex.

struct LOOP_s                     //Loop

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    struct HALFEDGE_s            *halfedge
;              // $p

    struct FACE_s                *face;                  // $p

    struct LOOP_s                *next;                  // $p

};

typedef struct LOOP_s *LOOP;

5.3.9 Fin

Note: Fins are referred to as halfedges in the PK Interface.

Field name	Type	Description
`attributes_features`	pointer0	Head of chain of attributes of fin
`loop`	pointer0	Loop of fin
`forward`	pointer0	Next fin around loop
`backward`	pointer0	Previous fin around loop
`vertex`	pointer0	Forward vertex of fin
`other`	pointer0	Next fin around edge, clockwise looking along edge
`edge`	pointer0	Edge of fin
`curve`	pointer0	For a non-dummy fin of a tolerant edge, this will be a trimmed SP-curve, otherwise null.
`next_at_vx`	pointer0	Next fin referencing the vertex of this fin
`sense`	pointer0	Positive (‘+’) if the fin direction is parallel to that of its edge, else negative (‘-’)

5.3.9.1 Dummy fins

An application will see edges as having any number of fins, including zero. However internally, they have at least two. This is so that the forward and backward vertices of an edge can always be found as edge->halfedge->vertex and edge->halfedge->other->vertex respectively - the first one being a positive fin, the second a negative fin. If an edge does not have both a positive and a negative externally-visible fin, dummy fins will exist for this purpose. Dummy fins have halfedge->loop = halfedge->forward = halfedge->backward = halfedge->curve = halfedge->next_at_vx = null . For example the boundaries of a sheet always have one dummy fin. See Section 5.3.9.2, “Fin chain at a vertex” for more information on fin chains at a vertex.

struct HALFEDGE_s  //Halfedge

    union  ATTRIB_FEAT_u         attributes_features;   // $p

    struct HALFEDGE_s           *forward;               // $p

    struct HALFEDGE_s           *backward;              // $p

    struct VERTEX_s             *vertex;                // $p

    struct HALFEDGE_s           *other;                 // $p

    struct EDGE_s               *edge;                  // $p

    union  CURVE_u               curve;                 // $p

    struct HALFEDGE_s           *next_at_vx;            // $p

    char                         sense;                 // $c

};

typedef struct HALFEDGE_s *HALFEDGE;

5.3.9.2 Fin chain at a vertex

The fin chain at a vertex only includes fins which are primary or secondary fins i.e edge->halfedge or edge->halfedge->other for some edge. All fins going into a vertex have that vertex as their halfedge->vertex but only those fins which are primary or secondary fins appear in the fin chains at the vertex. For any edge with a vertex or vertices, regardless of how many fins it has, the primary fin will be in the fin chain of the vertex towards which the edge points. The secondary fin will be in the fin chain of the vertex away from which the edge points. Any other fin will not appear in either fin chain at a vertex.

5.3.10 Vertex

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of vertex and `member_of_` feature of vertex
`halfedge`	pointer0	Head of singly-linked chain of fins referencing this vertex
`previous`	pointer0	Previous vertex in body
`next`	pointer0	Next vertex in body
`point`	pointer	Point of vertex
`tolerance`	double	Tolerance of vertex (null-double for accurate vertex)
`owner`	pointer	Owning body (for non-acorn vertices) or shell (for acorn vertices). If the vertex is in a child body and it’s not an acorn vertex then the field references the parent compound body.

union SHELL_OR_BODY_u

    struct BODY_s              *body;

    struct SHELL_s             *shell;

};

typedef union SHELL_OR_BODY_u SHELL_OR_BODY;

struct VERTEX_s                   //Vertex

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    struct HALFEDGE_s            *halfedge
;              // $p

    struct VERTEX_s              *previous;              // $p

    struct VERTEX_s              *next;                  // $p

    struct POINT_s               *point;                 // $p

    double                        tolerance;             // $f

    union SHELL_OR_BODY_u         owner;                 // $p

};

typedef struct VERTEX_s *VERTEX;

5.3.11 Edge

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer0	Head of chain of attributes of edge and `member_of_feature` of edge
`tolerance`	double	Tolerance of edge (null-double for accurate edges)
`halfedge`	pointer	Head of singly-linked chain of fins around edge
`previous`	pointer0	Previous edge in body or shell
`next`	pointer0	Next edge in body or shell
`curve`	pointer0	Curve of edge, zero for tolerant edge. If edge is accurate, but any of its vertices are tolerant, this will be a trimmed curve.
`next_on_curve`	pointer0	Next in chain of edges sharing the curve of this edge
`previous_on_curve`	pointer0	Previous in chain of edges sharing the curve of this edge
`owner`	pointer	Owning body (for non-wireframe edges) or shell (for wireframe edges). If the edge is in a child body and it is not a wireframe edge, then the field references the parent compound body.

struct EDGE_s                     //Edge

    int                           node_id;               // $d

    union  ATTRIB_FEAT_u          attributes_features;   // $p

    double                        tolerance;             // $f

    struct HALFEDGE_s            *halfedge
;              // $p

    struct EDGE_s                *previous;              // $p

    struct EDGE_s                *next;                  // $p

    union  CURVE_u                curve;                 // $p

    struct EDGE_s;               *next_on_curve          // $p

    struct EDGE_s                *previous_on_curve;     // $p

    union  SHELL_OR_BODY_u        owner;                 // $p

};

typedef struct EDGE_s *EDGE;

[back to top]

5.4 Associated Data

5.4.1 List

Field name	Type	Description
`node_id`	int	Zero
`list_type`	byte	Always
`notransmit`	logical	Ignore
`owner`	pointer	Owning part
`previous`	pointer0	Ignore
`next`	pointer0	Ignore
`list_length`	int	Length of list (>=0)
`block_length`	int	Length of each block of list. Always 20
`size_of_entry`	int	Ignore
`finger_index`	int	Any integer between 1 and list->list_length (set to 1 if length is zero). Ignore
`finger_block`	pointer	Any block e.g. the first one. Ignore
`list_block`	pointer	Head of singly-linked chain of pointer list blocks

Lists only occur in part data as the list of attributes referenced by a part.

typedef enum

    LIS_pointer = 4

    LIS_type_t;

union LIS_BLOCK_u

    struct POINTER_LIS_BLOCK_s    *pointer_block;

};

typedef union LIS_BLOCK_u     LIS_BLOCK;

union LIS_OWNER_u

    struct BODY_s                 *body;

    struct ASSEMBLY_s             *assembly;

    struct WORLD_s                *world;

};

typedef union LIST_OWNER_u    LIST_OWNER;

struct LIST_s                     //List Header

    int                           node_id;               // $d

    LIS_type_t                    list_type;             // $u

    logical                       notransmit;            // $l

    union  LIST_OWNER_u           owner;                 // $p

    struct LIST_s                *next;                  // $p

    struct LIST_s                *previous;              // $p

    int                           list_length;           // $d

    int                           block_length;          // $d

    int                           size_of_entry;         // $d

    int                           finger_index;          // $d

    union  LIS_BLOCK_u            finger_block;          // $p

    union  LIS_BLOCK_u            list_block;            // $p

};

typedef struct LIST_s *LIST;

5.4.2 Pointer_lis_block

Field name	Type	Description
`n_entries`	int	Number of entries in this block (0 <= n_entries <= 20). Only the first block may have n_entries = 0
`index_map_offset`	int	Shallbe set to 0
`next_block`	pointer0	Next pointer list block in chain
`entries[20]`	pointer	Pointers in block, those beyond n_entries shall be zero

When the pointer_lis_block is used as the root node in XT data containing more than one part, the restriction n_entries <= 20 does not apply.

The index_map_offset field is used for Indexed Transmit; applications writing XT data shall ensure this field is set to 0.

struct POINTER_LIS_BLOCK_s        //Pointer List

    int                           n_entries;            // $d

    int                           index_map_offset      // $d

    struct POINTER_LIS_BLOCK_s   *next_block;           // $p

    void                         *entries[ 1 ];         // $p[]

};

typedef struct POINTER_LIS_BLOCK_s *POINTER_LIS_BLOCK;

5.4.3 Att_def_id

Field name	Type	Description
`string[]`	char	String name e.g. "SDL/TYSA_COLOUR"

struct ATT_DEF_ID_s  //name field type for attrib def.

    char                          string[1];            // $c[]

};

typedef struct ATT_DEF_ID_s *ATT_DEF_ID;

5.4.4 Field_names

Field name	Type	Description
`names[]`	pointer	Array of field names - unicode or char

typedef union FIELD_NAME_u

    struct CHAR_VALUES_s         *name

    struct UNICODE_VALUES_s      *uname

};

    FIELD_NAME_t;

struct FIELD_NAME_s               //attribute field name

    union  FIELD_NAME_u           names[1];       // $p[]

};

typedef struct FIELD_NAME_s *FIELD_NAME;

5.4.5 Attrib_def

The XT Format provides a set of pre-defined attribute definitions known as system attribute definitions. See Appendix A, “System Attribute Definitions”, for more information on these.

Attribute definitions have the following form in the XT format:

Field name	Type	Description
`next`	pointer0	Next attribute definition. This can be ignored, except in partition data.
`identifier`	pointer	Pointer to a string name
`type_id`	int	Numeric id, e.g. 8001 for color. 9000 for user-defined attribute definitions
`actions[8]`	byte	Required actions on various events
`field_names`	pointer	Names of fields (unicode or char)
`legal_owners[14]`	logical	Allowed owner types
`fields[]`	byte	Array of field types. Note that the number of fields is given by the length of the variable length part of this node, i.e. the integer following the node type in the XT data.

The legal_owners array is an array of logicals determining which node types may own this type of attribute.

e.g. if faces are allowed attrib_def -> legal_owners [SCH_fa_owner] = true .

Note that if the XT data contains user fields, the ‘fields’ field of an attribute definition may contain extra values, set to zero. These are to be ignored.

The ‘actions’ field in an attribute definition defines the behaviour of the attribute when an event (rotate, scale, translate, reflect, split, merge, transfer, change) occurs. The actions are in table F.49:

Action	Explanation
`do_nothing`	Leave attribute as it is
`delete`	Delete the attribute
`transform`	Transform the transformable fields (point, vector, direction, axis) by appropriate part of transformation
`propagate`	Copy attribute onto split-off node
`keep_sub_dominant`	Move attribute(s) from deleted node onto surviving node in a merge, but any such attributes already on the surviving node are deleted
`keep_if_equal`	Keep attribute if present on both nodes being merged, with the same field values
`combine`	Move attribute(s) from deleted node onto surviving node, in a merge

The XT attribute classes 1-7 correspond as follows:

	split	merge	transfer	change	rotate	scale	translate	reflect
class 1	propagate	keep_equal	do_nothing	do_nothing	do_nothing	do_nothing	do_nothing	do_nothing
class 2	delete	delete	delete	delete	do_nothing	delete	do_nothing	do_nothing
class 3	delete	delete	delete	delete	delete	delete	delete	delete
class 4	propagate	keep_equal	do_nothing	do_nothing	transform	transform	transform	transform
class 5	delete	delete	delete	delete	transform	transform	transform	transform
class 6	propagate	combine	do_nothing	do_nothing	do_nothing	do_nothing	do_nothing	do_nothing
class 7	propagate	combine	do_nothing	do_nothing	transform	transform	transform	transform

typedef enum

    SCH_rotate      = 0,

    SCH_scale       = 1,

    SCH_translate   = 2,

    SCH_reflect     = 3,

    SCH_split       = 4,

    SCH_merge       = 5,

    SCH_transfer    = 6,

    SCH_change      = 7,

    SCH_max_logged_event   //last entry; value in $d[] code for actions

    SCH_logged_event_t;

typedef enum

    SCH_do_nothing        = 0,

    SCH_delete            = 1,

    SCH_transform         = 2,

    SCH_propagate         = 3,

    SCH_keep_sub_dominant = 4,

    SCH_keep_if_equal     = 5,

    SCH_combine           = 6

    SCH_action_on_fields_t;

typedef enum

    SCH_as_owner = 0,

    SCH_in_owner = 1,

    SCH_by_owner = 2,

    SCH_sh_owner = 3,

    SCH_fa_owner = 4,

    SCH_lo_owner = 5,

    SCH_ed_owner = 6,

    SCH_vx_owner = 7,

    SCH_fe_owner = 8,

    SCH_sf_owner = 9,

    SCH_cu_owner = 10,

    SCH_pt_owner = 11,

    SCH_rg_owner = 12,

    SCH_fn_owner = 13,

    SCH_max_owner  //last entry; value in $l[] for                    .legal_owners

    SCH_attrib_owners_t;

typedef enum

    SCH_int_field       = 1,

    SCH_real_field      = 2,

    SCH_char_field      = 3,

    SCH_point_field     = 4,

    SCH_vector_field    = 5,

    SCH_direction_field = 6,

    SCH_axis_field      = 7,

    SCH_tag_field       = 8,

    SCH_pointer_field   = 9,

    SCH_unicode_field   = 10

    SCH_field_type_t;

struct ATTRIB_DEF_s               //attribute definition

    struct ATTRIB_DEF_s          *next;               // $p

    struct ATT_DEF_ID_s          *identifier;         // $p

    int                           type_id;            // $d

    SCH_action_on_fields_t        actions             // $u[8]

    [(int)SCH_max_logged_event];                      // $u[8]

    struct FIELD_NAMES_s         *field_names         // $p

    logical                       legal_owners        // $l[14]

     [(int)SCH_max_owner];                            //$l[14]

    SCH_field_type_t              fields[1];          // $u[]

};

typedef struct ATTRIB_DEF_s *ATTRIB_DEF;

5.4.6 Attribute

Field name	Type	Description
`node_id`	int	Identifier
definition	pointer	Attribute definition
`owner`	pointer	Attribute owner
`next`	pointer0	Next attribute, feature, or `member_of_feature`
`previous`	pointer0	Previous ditto
`next_of_type`	pointer0	Next attribute of this type in this part
`previous_of_type`	pointer0	Previous attribute of this type in this part
`fields[]`	pointer	Fields, of type int_values etc. The number of fields is given by the length of the variable part of the node. There may be no fields.

The attributes of a node are chained using the next and previous pointers in the attribute. The attributes_ features pointer in the node points to the head of this chain. This chain also contains the member_of_ feature of the node.

Attributes within the same part, with the same attribute definition, are chained together by the next_of_type and previous_of_type pointers. The part points to the head of this chain as follows. The attribute_chains pointer in the part points to a list which contains the heads of these attribute chains, one for each attribute definition which has attributes in the part. The list may be null.

Note that the attributes_ features chains in parts, features and nodes contain the following types of node:

Part: attributes and features.
Feature: attributes.
Node: attributes and member_of_feature .

Fields of type ‘pointer’ can be used in Parasolid V12.0, but they are always transmitted as empty.

union ATTRIBUTE_OWNER_u

    struct ASSEMBLY_s            *assembly;

    struct INSTANCE_s            *instance;

    struct BODY_s                *body;

    struct SHELL_s               *shell;

    struct REGION_s              *region;

    struct FACE_s                *face;

    struct LOOP_s                *loop;

    struct EDGE_s                *edge;

    struct HALFEDGE_s            *halfedge
;

    struct VERTEX_s              *vertex;

    union  SURFACE_u              Surface;

    union  CURVE_u                Curve;

    struct POINT_s               *point;

    struct FEATURE_s
             *feature;

};

typedef union ATTRIBUTE_OWNER_u ATTRIBUTE_OWNER;

union FIELD_VALUES_u

    struct INT_VALUES_s          *int_values;

    struct REAL_VALUES_s         *real_values;

    struct CHAR_VALUES_s         *char_values;

    struct POINT_VALUES_s        *point_values;

    struct VECTOR_VALUES_s       *vector_values;

    struct DIRECTION_VALUES_s    *direction_values;

    struct AXIS_VALUES_s         *axis_values;

    struct TAG_VALUES_s          *tag_values;

    struct UNICODE_VALUES_s      *unicode_values;

};

typedef union FIELD_VALUES_u FIELD_VALUES;

struct ATTRIBUTE_s                //Attribute

    int                          node_id;              // $d

    struct ATTRIB_DEF_s         *definition;           // $p

    union  ATTRIBUTE_OWNER_u     owner;                // $p

    union  ATTRIB_FEAT_u         next;                 // $p

    union  ATTRIB_FEAT_u         previous;             // $p

    struct ATTRIBUTE_s          *next_of_type;         // $p

    struct ATTRIBUTE_s          *previous_of_type;     // $p

    union  FIELD_VALUES_u        fields[1];            // $p[]

};

typedef struct ATTRIBUTE_s *ATTRIBUTE;

5.4.7 Int_values

Field name	Type	Description
`values[]`	int	Integer values

struct INT_VALUES_s                //Int values

    int                            values[1];           // $d[]

};

typedef struct INT_VALUES_s *INT_VALUES;

5.4.8 Real_values

Field name	Type	Description
`values[]`	double	Real values

struct REAL_VALUES_s               //Real values

    double                         values[1];           // $f[]

};

typedef struct REAL_VALUES_s *REAL_VALUES;

5.4.9 Char_values

Field name	Type	Description
`values[]`	char	Character values

struct CHAR_VALUES_s               //Character values

    char                           values[1];           // $c[]

};

typedef struct CHAR_VALUES_s *CHAR_VALUES;

5.4.10 Unicode_values

Field name	Type	Description
`values[]`	short	Unicode character values

struct UNICODE_VALUES_s            //Unicode character values

    short                          values[1];           // $w[]

};

typedef struct UNICODE_VALUES_s *UNICODE_VALUES;

5.4.11 Point_values

Field name	Type	Description
`values[]`	vector	Point values

struct POINT_VALUES_s              //Point values

    vector                         values[1];           // $v[]

};

typedef struct POINT_VALUES_s *POINT_VALUES;

5.4.12 Vector_values

Field name	Type	Description
`values[]`	vector	Vector values

struct VECTOR_VALUES_s             //Vector values

    vector                         values[1];           // $v[]

};

typedef struct VECTOR_VALUES_s *VECTOR_VALUES;

5.4.13 Direction_values

Field name	Type	Description
`values[]`	vector	Direction values

struct DIRECTION_VALUES_s          //Direction values

    vector                         values[1];           // $v[]

};

typedef struct DIRECTION_VALUES_s *DIRECTION_VALUES;

5.4.14 Axis_values

Field name	Type	Description
`values[]`	vector	Axis values

struct AXIS_VALUES_s              //Axis values

    vector                         values[1];           // $v[]

};

typedef struct AXIS_VALUES_s *AXIS_VALUES;

5.4.15 Tag_values

Field name	Type	Description
`values[]`	int	Integer tag values

struct TAG_VALUES_s                //Tag values

    int                            values[1];           // $t[]

};

typedef struct TAG_VALUES_s *TAG_VALUES;

The tag field type and the tag_values node are not available for use in user-defined attributes, they occur only in certain system attributes.

5.4.16 Feature

Note: Features are referred to as ‘groups’ in the PK Interface.

Field name	Type	Description
`node_id`	int	Identifier
`attributes_features`	pointer	Head of chain of attributes of this feature
`owner`	pointer	Owning part
`next`	pointer0	Next feature or attribute
`previous`	pointer0	Previous feature or attribute
`type`	byte	Type of node allowed in feature
`first_member`	pointer0	Head of chain of `member_of_` feature nodes in feature

The groups in a part are chained by the next and previous pointers in a group. The attributes_ features pointer in the part points to the head of the chain. This chain also contains the attributes attached directly to the part - groups and attributes are intermingled in this chain, the order is not significant.

Each group has a chain of member_of_ feature. These are chained together using the next_member and previous_member pointers. The first_member pointer in the feature points to the head of the chain. Each member_of_ feature has an owning_ feature pointer which points back to the feature.

Each member_of_ feature has an owner pointer which points to a node. Thus the feature references its member nodes via the member_of_feature .

The member_of_ feature which refer to a particular node are chained using the next and previous pointers in the member_of_ feature. The attributes_ features pointer in the node points to the head of this chain. This chain also contains the attributes attached to the node.

typedef enum

    SCH_instance_fe   = 1,

    SCH_face_fe       = 2,

    SCH_loop_fe       = 3,

    SCH_edge_fe       = 4,

    SCH_vertex_fe     = 5,

    SCH_surface_fe    = 6,

    SCH_curve_fe      = 7,

    SCH_point_fe      = 8,

    SCH_mixed_fe      = 9,

    SCH_region_fe     = 10,

    SCH_pf_pline_fe   = 11,

    SCH_feature_fe    = 12

    } SCH_feature_type_t;

struct FEATURE_s  //Feature

    int                          node_id;               // $d

    union  ATTRIB_FEAT_u         attributes_features;   // $p

    union  PART_u                owner;                 // $p

    union  ATTRIB_FEAT_u         next;                  // $p

    union  ATTRIB_FEAT_u         previous;              // $p

    SCH_feature_type_t           type;                  // $u

    struct MEMBER_OF_FEATURE_s  *first_member;          // $p

};

typedef struct FEATURE_s *FEATURE;

5.4.17 Member_of_feature

Field name	Type	Description
`dummy_node_id`	int	Entity label
`owning_feature`	pointer	Owning feature
`owner`	pointer	Referenced member of feature
`next`	pointer0	Next attribute, feature or `member_of_` feature
`previous`	pointer0	Previous ditto
`next_member`	pointer0	Next `member_of_` feature in this feature
`previous_member`	pointer0	Previous ditto

union FEATURE_MEMBER_u

    struct INSTANCE_s            *instance;

    struct FACE_s                *face;

    struct REGION_s              *region;

    struct LOOP_s                *loop;

    struct EDGE_s                *edge;

    struct VERTEX_s              *vertex;

    union  SURFACE_u              surface;

    union  CURVE_u                curve;

    struct POINT_s               *point;

struct FEATURE_s  *feature;

};

typedef union FEATURE_MEMBER_u FEATURE_MEMBER;

struct MEMBER_OF_FEATURE_s //Member of feature

   int                             dummy_node_id;        // $d

   struct FEATURE_s               *owning_feature;       // $

   union  FEATURE_MEMBER_u         owner;                // $p

   union  ATTRIB_FEAT_u            next;                 // $p

   union  ATTRIB_FEAT_u            previous;             // $p

   struct MEMBER_OF_FEATURE_s     *next_member;          // $p

   struct MEMBER_OF_FEATURE_s     *previous_member;      // $p

};

typedef struct MEMBER_OF_FEATURE_s *MEMBER_OF_FEATURE;

5.4.18 Part_XMT_block

Field name	Type	Description
`n_entries`	int	Number of entries in this block. (`n_entries` >1)
`index_map_offset`	int	Must be set to 0
`index_map`	pointer0	Must be set to null
`schema_embedding_map`	pointer0	Must be set to null
`mesh_offset_data`	pointer0	Data for embedded meshes. If the XT file does not contain embedded meshes, this field must be set to null.
`entries[]`	pointer	Pointers in block

The PART_XMT_BLOCK must be the root node in XT data containing more than one part,

The fields index_map_offset , index_map , and schema_embedding_map are used for Indexed Transmit.

The mesh_offset_data field is used for embedded mesh data.

struct PART_XMT_BLOCK_s //Part list

int                              n_entries;              //$d

unsigned                         index_map_offset;       //$d

struct INT_VALUES_s             *index_map;              //$p

struct INT_VALUES_s             *schema_embedding_map;   //$p

struct MESH_OFFSET_DATA_s       *mesh_offset_data;       //$p

union PART_u                     entries[1];             //$p[]

};

typedef struct PART_XMT_BLOCK_s *PART_XMT_BLOCK;

5.4.19 Mesh_offset_data

The MESH_OFFSET_DATA node is used for embedded mesh data. It is the second node in an XT file with embedded meshes. At most, there can only be one MESH_OFFSET_DATA node.

Field Name	Data Type	Description
`mesh_index_map`	pointer0	Must be set to an `offset_values` node
`schema_data`	pointer0	See Section 5.4.19.2, “Schema_data” for information
`schema_data_offset_high`	int	Must be present
`schema_data_offset_low`	int	Must be present

The schema_data field must be present if the XT data contains embedded schema information, otherwise it must be set to null.

The schema_data_offset_high and schema_data_offset_low fields must be present and indicate either the offset of the schema_data node (if present), or the offset of the terminator.

struct MESH_OFFSET_DATA_s //Mesh offset data

struct OFFSET_VALUE_s    *mesh_index_map;           //$p

struct SCHEMA_DATA_s     *schema_data;              //$p

unsigned                 *schema_data_offset_high;  //$d

unsigned                 *schema_data_offset_low ;  //$d

};

typedef struct MESH_OFFSET_DATA_s *MESH_OFFSET_DATA;

5.4.19.1 Offset_values

The OFFSET_VALUES node contains the offset values of each PSM_MESH node. These offset values must be in the same order as the PSM_MESH nodes in the XT data. If this node is present, it must be the third node in the XT data.

Field Name	Data Type	Description
`values[]`	int	Offset values in high and low pairs

struct OFFSET_VALUES_s     //Offset values

unsigned    values[1];     //$d[]

};

typedef struct OFFSET_VALUES_s *OFFSET_VALUES;

5.4.19.2 Schema_data

The SCHEMA_DATA node must be present if the XT data contains embedded schema information. The SCHEMA_DATA node chains one NODE_MAP node per node type used in the mesh data section of the XT data (i.e between the first PSM_MESH node and the last node before the SCHEMA_DATA node).

There is a NEW_NODE_MAP node defining the following node types:

PSM_MESH
INTEGER_TOOTH
INTEGER_COMB
VECTOR_TOOTH
VECTOR_COMB

These node types are relative to the defined base schema, currently SCH_13006. See Section 2.1.2, “Embedded schemas” for more information.

struct SCHEMA_DATA_s //Schema data

union NODE_MAP_u   node_map;   //$p

};

typedef struct SCHEMA_DATA_s *SCHEMA_DATA;

The SCHEMA_DATA node is followed by the NODE_MAP, FIELD_MAP, and SCHEMA_CHAR_VALUES nodes. These nodes will always be at the end of the embedded mesh file and indicate whether an embedded mesh file was saved using an embedded schema.

5.4.19.3 Node_map union

union NODE_MAP_u

struct ANY_NODE_MAP_s *any;

struct NEW_NODE_MAP_s *new;

struct MOD_NODE_MAP_s *mod;

struct OLD_NODE_MAP_s *old;

};

typedef union NODE_MAP_u NODE_MAP;

5.4.19.4 Node map nodes

All node map nodes share the following common fields:

Field Name	Data Type	Description
`next`	pointer0	Next node map in chain
exemplar_offset_high	int	Offset values of the first node of `node_type` in the XT data
exemplar_offset_low	int	Offset values of the first node of `node_type` in the XT data
node_type	short	Node type

5.4.19.5 Any_node_map

struct ANY_NODE_MAP_s //Any node map

union NODE_MAP_u             next;                  //$p

unsigned                     exemplar_offset_high;  //$d

unsigned                     exemplar_offset_low;   //$d

short                        node_type;             //$n

};

typedef struct ANY_NODE_MAP_s  *ANY_NODE_MAP;

5.4.19.6 Old_node_map

struct OLD_NODE_MAP_s == ANY_NODE_MAP_s //Unchanged node map

union NODE_MAP_u             next;                  //$p

unsigned                     exemplar_offset_high;  //$d

unsigned                     exemplar_offset_low;   //$d

short                        node_type;             //$n

};

typedef struct OLD_NODE_MAP_s *OLD_NODE_MAP;

5.4.19.7 New_node_map

Field Name	Data Type	Description
vla_field_xmt_code	logical	Whether the variable length array field (if present) should be saved to XT. If this field is not present, the value is set to false.
name	pointer	Points to the schema character values node that contain the node name.
description	pointer	Points to the schema character values node that contain the description.
field_maps[1]	pointer	Array of new field maps

struct NEW_NODE_MAP_s == ANY_NODE_MAP_s //New node map

union NODE_MAP_u             next; $p

unsigned                     exemplar_offset_high;  //$d

unsigned                     exemplar_offset_low;   //$d

short                        node_type;             //$n

logical                      vla_field_xmt_code;    //$l

struct SCHEMA_CHAR_VALUES_s *name;                  //$p

struct SCHEMA_CHAR_VALUES_s *description;           //$p

struct NEW_FIELD_MAP_s      *field_maps[1];         //$p[]

};

typedef struct NEW_NODE_MAP_s *NEW_NODE_MAP;

5.4.19.8 Modified_node_map

Field Name	Data Type	Description
vla_field_xmt_code	logical	Whether the variable length array field (if present) is transmitted. If this field is not present, the value is set to false.
field_maps[1]	pointer	Array of field maps

struct MOD_NODE_MAP_s == ANY_NODE_MAP_s          //Modified node map

union NODE_MAP_u             next;                  //$p

unsigned                     exemplar_offset_high;  //$d

unsigned                     exemplar_offset_low;   //$d

short                        node_type;             //$n

logical                      vla_field_xmt_code;    //$l

union FIELD_MAP_u            field_maps[1];         //$p[]

};

typedef struct MOD_NODE_MAP_s *MODE_NODE_MAP;

5.4.19.9 Field_map union

union FIELD_MAP_u

struct NEW_FIELD_MAP_s *new;

struct OLD_FIELD_MAP_s *old;

};

typedef union FIELD_MAP_u FIELD_MAP;

5.4.19.10 Old_field_map

Field Name	Data Type	Description
`base_index`	byte	The field number this field used to be in the baseline schema

struct OLD_FIELD_MAP_s // Old field map

SCH_byte_t               base_index;    //$u

};

typedef struct OLD_FIELD_MAP_s *OLD_FIELD_MAP;

5.4.19.11 New_field_map

Field Name	Data Type	Description
`name`	pointer	Points to the schema character values node that contains the field name.
ptr_class	short	Node type or class of the field if it is a pointer field
n_elts	int	Number of elements for that field
type	pointer	Points to a schema character values node that contains the field type.

struct NEW_FIELD_MAP_s // New field map

struct SCHEMA_CHAR_VALUES_s *name;      //$p

short                        ptr_class; //$n

int                          n_elts;    //$d

struct SCHEMA_CHAR_VALUES_s *type;      //$p

};

typedef struct NEW_FIELD_MAP_s *NEW_FIELD_MAP;

5.4.19.12 Schema_char_values

Field Name	Data Type	Description
`values[]`	char	Character values

struct SCHEMA_CHAR_VALUES_s     //Schema character values

char values[1];     //$c[]

};

typedef struct SCHEMA_CHAR_VALUES_s *SCHEMA_CHAR_VALUES;

[back to top]

<<< Model Structure

Chapters

Nodes and Classes >>>

Contents

5.1 Underlying types

5.2 Geometry

5.2.1 Curves

5.2.1.1 Line

5.2.1.2 Circle

5.2.1.3 Ellipse

5.2.1.4 B_CURVE (B-spline curve)

5.2.1.5 Intersection

5.2.1.6 Trimmed_curve

5.2.1.7 PE_CURVE (Foreign geometry curve)

5.2.1.8 SP_CURVE

5.2.1.9 Polyline

5.2.2 Surfaces

5.2.2.1 Plane

5.2.2.2 Cylinder

5.2.2.3 Cone

5.2.2.4 Sphere

5.2.2.5 Torus

5.2.2.6 Blended_edge (Rolling ball blend)

5.2.2.7 Blend_bound (Blend boundary surface)

5.2.2.8 Offset_surf

5.2.2.9 B_surface

5.2.2.10 Swept_surf

5.2.2.11 Spun_surf

5.2.2.12 PE_surf (Foreign geometry surface)

5.2.3 Mesh Surfaces

5.2.3.1 PSM mesh

5.2.3.2 Position pool

5.2.3.3 Position indices

5.2.3.4 Normal pool

5.2.3.5 Normal indices

5.2.4 Lattices

5.2.4.1 Irregular lattice node

5.2.5 Point

5.2.6 Transform

5.2.7 Comb nodes

5.2.7.1 VECTOR_COMB nodes

5.2.7.2 INTEGER_COMB nodes

5.2.7.3 REAL_COMB nodes

5.2.8 Curve, surface and lattice senses

5.2.9 Geometric_owner

5.3 Topology

5.3.1 World

5.3.2 Assembly

5.3.3 Instance

5.3.4 Body

5.3.4.1 Attaching geometry to topology

5.3.5 Region

5.3.6 Shell

5.3.7 Face

5.3.8 Loop

5.3.8.1 Isolated loops

5.3.9 Fin

5.3.9.1 Dummy fins

5.3.9.2 Fin chain at a vertex

5.3.10 Vertex

5.3.11 Edge

5.4 Associated Data

5.4.1 List

5.4.2 Pointer_lis_block

5.4.3 Att_def_id

5.4.4 Field_names

5.4.5 Attrib_def

5.4.6 Attribute

5.4.7 Int_values

5.4.8 Real_values

5.4.9 Char_values

5.4.10 Unicode_values

5.4.11 Point_values

5.4.12 Vector_values

5.4.13 Direction_values

5.4.14 Axis_values

5.4.15 Tag_values

5.4.16 Feature

5.4.17 Member_of_feature

5.4.18 Part_XMT_block

5.4.19 Mesh_offset_data

5.4.19.1 Offset_values

5.4.19.2 Schema_data