B-Spline Curves and Surfaces   

<<< Working with Sheets and Wires Chapters Convergent Modeling >>>

Contents

[back to top]

7.1 Introduction

Wherever possible, Parasolid uses analytic geometry in its models. For example, curves such as circles, ellipses and lines, and surfaces such as spheres, tori and cones are represented using geometry that can be described by an equation. Using analytic geometry as much as possible gives Parasolid unparalleled speed and economy of storage.

There are times, however, when geometry cannot be represented by analytic entities. If possible, other types of geometry are used (such as swept or spun surfaces), but when even this is not possible, NURBs-based ( Non- Uniform Rational B- splines) B-geometry is used instead. Parasolid offers two forms of B-geometry: B-curves and B-surfaces. Unlike analytic geometry, B-geometry is defined over a finite region of space.

B-curves and B-surfaces are fully integrated into Parasolid, so you can attach them to edges and faces, and apply any relevant Parasolid operation to them, just as you would any other type of curve or surface. This integration is so tight that in most circumstances there is no reason why users even need be aware they are using B-geometry. However, in addition, Parasolid provides functionality to let you work explicitly with B-geometry. This chapter describes the functionality that is available.

 

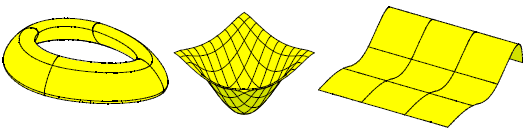
Figure 7-1 Examples of B-surfaces

[back to top]

7.2 Creating B-geometry

Parasolid’s use of B-geometry is kept to a minimum; wherever possible, other types of geometry are used during operations that create geometry. However, if you explicitly need to create B-geometry, Parasolid provides the following methods:

 

Method

Description

Supplying B-spline data

You can supply B-splines (in the form of control points and knot vectors), and Parasolid can create B-curves and B-surfaces directly from this data.

Supplying piecewise data

You can supply independent segments of surface or curve data, in either Bezier, Hermite, polynomial or Taylor series format. Parasolid can piece these individual segments together to create the appropriate B-geometry.

Splining

You can create B-geometry with data that is not as rich as B-spline or piecewise data by using Parasolid’s general splining functionality. You supply a series (for a B-curve) or a mesh (for a B-surface) of points, and Parasolid creates a curve or surface either by interpolating through the supplied points or by fitting to them within a specified tolerance. You can control the final appearance of the geometry using controls such as clamping conditions.

Curve and surface fitting

You can build B-curves and B-surfaces from a set of points sampled from existing curves or surfaces. This functionality is principally used to improve the quality of existing geometry; for example, after importing curve or surface data into Parasolid, you may decide to rebuild data that is not C2-continuous using these functions. You can also create B-geometry using only the definition of a curve or surface, rather than actual geometric data.

Constrained surfaces

You can create B-surfaces from a cloud of points and, optionally, normals, which constrain the shape of the resulting B-surface. To further constrain the surface, you can also supply parameterisation information.

Converting from other geometry

You can convert any piece of geometry into B-geometry. This can be useful if you want to output your data for use in non-Parasolid based applications that use less efficient methods of storing data.

[back to top]

7.3 Modelling with B-geometry

While performing modelling operations, Parasolid treats B-geometry just like any other type of geometry, allowing you to apply relevant operations to models that have attached B-curves and B-surfaces. In addition, Parasolid offers a range of modelling functionality that is intended specifically for use with B-geometry.

 

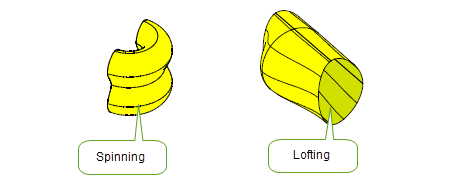
Figure 7-2 modelling with B-geometry

Some of the modelling operations that can be performed with B-geometry are as follows:

 

Operation

Description

Sweeping and spinning

Parasolid can create B-surfaces by sweeping or spinning a previously created B-curve.

Lofting

Parasolid can create B-surfaces by lofting between a set of pre-defined B-curves. Parasolid’s generic lofting functionality is described in more detail in Chapter 9, “Building Bodies from Profiles”.

Parasolid contains a variety of options to control the shape of the lofted surface.

Extracting isoparam curves

Parasolid can create B-curves along constant parameter lines from a B-surface.

Curve joining

Parasolid can join a number of B-curves to form a single B-curve.

Parasolid allows you to simplify the geometry in a body by converting rational B-curves and B-surfaces to non-rational B-curves and B-surfaces. You can also convert non-rational B-curves to lines or circles, and non-rational B-surfaces to planes, cylinders, cones, spheres or tori.

[back to top]

<<< Working with Sheets and Wires Chapters Convergent Modeling >>>