Implementing an FG System

2.1 Introduction

This chapter explains the process whereby the user creates FG evaluators and links them into Parasolid. An overall description of this procedure is given in Chapter 1, “Introduction and Summary”.

[back to top]

2.2 Writing the FG module

[back to top]

2.2.1 An example evaluator

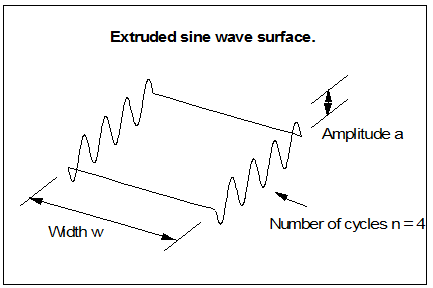
Let’s start by taking an example of a surface for which we want to write an evaluator:

The surface function:

P( u, v ) = ( u, v, a sin(2 pi u) )

generates an extruded sine wave surface. If we further allow the parameter ranges to be:

U in the range [ 0, n ]V in the range [ 0, w ]

then we generate the surface shown in the diagram below:

To implement an evaluator function for this surface we have to make some basic design decisions :

We supply the parameters a, n and w as real numbers submitted through the interface
We identify the generic surface by the key EDS/corrugated (the key should give an indication of the source of the evaluator - in this case Electronic Data Systems)
The code for the evaluator is linked to Parasolid (so that we can access the evaluator function by its address in memory)

The tasks we have to complete in order to implement this surface are :

Enable the initialization of a corrugated surface - (through function FGCRSU)
Supply its parameter limits to Parasolid - (through function FGPRSU)
Enable evaluations of the surface - (through function FGEVSU)

[back to top]

2.2.2 Evaluator initialization

Our surface is requested by a call to function PK_FCURVE_create. The arguments to this function should be:

Keylen is 14 (i.e. the number of characters in the evaluator key string),
Key is EDS/corrugated
nspace is 1 (the minimum value)
nints is 0
ivals is a null pointer
nreals is 3
rvals is a pointer to a real array containing (a, n, w)

This call generates a call to the function FGCRSU with essentially the same arguments, except that a double array of length 1 has been allocated by Parasolid for initialization by FGCRSU.

In FGCRSU a section of code is added to recognize our corrugated surface and enable evaluations of it. The code which achieves this is :

if( keycmpu( “SDL/corrugated”, key, keylen )){if (( *kir == 3 ) &&  /*corrugated evaluator requires 3 reals*/  ( ki_reals[1] > 0.0 ) &&   /*of which last two are positive*/  ( ki_reals[2] > 0.0 ))              *(surface_evaluator *) fg_data = corrugated;else *ifail = FGRERR;        /*...otherwise real data error*/}

Note: 1. The function FGCRCU performs the initialization of curve evaluators, receiving the same arguments and performing the same tasks.

Note: 2. The function


keycmpu

does a string comparison between the supplied key and the valid key for our surface. This function is part of the sample code. A straightforward C string comparison does not work here since, for FORTRAN compatibility reasons, the key has no standard C null terminator.

Note: 3. It is at this point in the code that any validation of data needs to be implemented - a successful call to FGCRSU should indicate that valid evaluations are available. In this case three real data items must be available of which the final two (the number of cycles, n, and the width of the surface , w) need to be positive. If the real data supplied through the interface does not fit this form, then the ifail return code is set to FGRERR to indicate unsatisfactory real data.

Note: 4. The type definition surface_evaluator is: typedef void (* surface_evaluator)()

Once the data has been validated, the address of the evaluator function is stored in the fg_data space that was requested. The evaluator is called by a call to this address. All future references to this evaluator (by functions FGPRSU, FGEVSU) are made by passing the fg_data array, as initialized here - the key is no longer supplied.

Note: 5. If an evaluator is written which uses secure data stored in the fg_data array, FGCRSU needs to implement the loading of this data. Evaluators of this type should have a key which itself contains the filename/database entry where the data can be found. For example, a key


EDS/Gordon/Example1

could indicate that the Gordon surface evaluator should be used with data loaded from file


Example1

Note: 6. FGCRSU is only called once per FG surface. The structure of our example could get unwieldy if many tens or hundreds of surfaces were implemented. In this case some means of avoiding a lot of string comparisons would be useful, but is not critical.

Note: 7. FGCRSU is called whenever a foreign surface is to be initialized for use in Parasolid. This can happen directly when a user calls up a new foreign surface using PK_FSURF_create, or indirectly when a user loads an archived part into Parasolid using PK_PART_receive, when FGCRSU is called once for every foreign surface present in the part.

[back to top]

2.2.3 Parameter properties function

Once a surface is successfully initialized by a call to FGCRSU, a call is made to function FGPRSU so that Parasolid can be informed of the parametric properties of the surface. In our example code the relevant code is :

{  surface_evaluator eval;  eval = *(surface_evaluator *)fg_data;  *ifail = FGPROP;              /* initialize properties to defaults*/  if ( eval == corrugated )  {                             /* establish ‘corrugated’ properties*/    range[0] = 0.0;             /* low u value    */    range[1] = ki_reals[1];     /* high u value   */    range[2] = 0.0;             /* low v value    */    range[3] = ki_reals[2];     /* high v value   */    period[0] = FGPRBD;         /* bounded u parametrisation */    period[1] = FGPRBD;         /* bounded v parametrisation */    *ifail = FGOPOK;  }......

Note: 1. The parameter ranges [0,n] and [0,w] are returned to Parasolid.

Note: 2. The surface key is no longer available, so our surface is recognized by the address stored in fg_data.

Note: 3. The


period

arguments must be set as shown, to FGPRBD - ‘not periodic’. At the current Parasolid version, periodic surfaces are not allowed so this argument is for future extensions.

Note: 4. Default parameter properties may be assumed by setting the return ifail code to FGPROP. These properties are u and v ranges both [0, 1] and periodicity flags both FGPRBD.

Note: 5. The corresponding function for curves, FGPRCU, behaves in a very similar way. The only differences are that the range array only has two entries, range[0] and range[1], for low and high values of the curve's parametrisation, and that only period[0] needs to be initialized to FGPRBD to indicate that the t parametrisation is non-periodic. Again, default properties may be used by setting the return code to FGPROP.

[back to top]

2.2.4 The evaluation function

Enabling evaluations of the surface

Evaluations of surfaces are routed through function FGEVSU. In our example this is implemented as :

eval = *(surface_evaluator *) fg_data;                                    /* initialize evaluator function*/*ifail = FGOPOK;                         /* initialize ifail */(*eval)( ki_ints, ki_reals, fg_data, u, v,                                           /* & call evaluator */     nu, nv, triang, results, ifail ); }

Note: 1. We set ifail to ‘success’ so that evaluators only have to set other outcomes.

Note: 2. FGEVSU then simply routes the request directly to our evaluator function. Clearly this mechanism depends upon evaluators being written with the same arguments as FGEVSU. In existing systems this may well not be possible. In these cases the call to the evaluator needs to be made and the results processed, by this function, into the form which Parasolid is expecting.

Note: 3. The performance of this linkage to the external evaluators is quite critical to the performance of FG within Parasolid - many thousands of calls are made to the evaluator in a modeling session. Therefore every effort should be made to optimize this function. In FORTRAN, for example, storage of an integer in fg_data followed by a computed GOTO here works.

The corrugated evaluator function.

The evaluator call supplies arguments as follows :

Pointers to the three data arrays which the evaluator can use ( ki_ints, ki_reals, fg_data )
Parameter position (u, v). Parasolid ensures that only parameter values within the parameter range of the surface are requested, so no tests need to be done for this.
Derivative specification ( nu, nv, triang ) which refers to the number of u derivatives requested, the number of v derivatives requested, and the triangular flag.
The results array is supplied for the evaluator to return its results. Each position or derivative is stored in three elements of this array.

Let’s look at a section of the sample corrugated evaluator code:

if ( su_dP_du( &n, *nu, *nv, *triang )){  /*    compute : Pu  */  results[n++] = 1.0;  results[n++] = 0.0;  results[n]    = two_pi * A * cos(*u * two_pi);}

and later on after all evaluations are complete...

*ifail = su_check_params( *ifail, *nu, *nv, *triang );

Note: 1. The decision as to whether a particular derivative is required, and where it should be returned in the results array, is not entirely straightforward. Therefore we have provided a set of utility functions for this purpose. In the example above, su_dP_du returns TRUE if the dP/du derivative is requested and n points to the correct position in the results array. More details on these issues are given below.

Note: 2. The function su_check_params sets ifail to FGEVIN if the evaluation requested could not be completely fulfilled. It assumes that evaluators are written to supply up to and including all second derivatives ( the minimum requirement ). Cases where Parasolid asks for more than the evaluator can supply may occur, for example, if a surface is created which is the offset of an FG surface. In these cases FGEVIN alerts Parasolid to the need to approximate the missing derivatives. Parasolid recognizes missing derivatives by checking that no assignment has been made to the relevant entries in the results array, so it is important NOT to set elements of the results array that have not been successfully calculated.

Note: 3. The corresponding function for curves, FGEVCU, has been similarly coded but is more straightforward in that the derivative request is a single argument, nderiv, for the number of t derivatives requested as opposed to the surface derivative request (nu, nv, triang) for the numbers of u and v derivatives requested along with the triangular flag.

[back to top]

2.2.5 Derivative specifications and output

The results of an evaluation are returned in the results array passed down to the evaluator. The specification of the numbers of derivatives required is supplied by means of the nu , nv and triang arguments. The meanings of these is as follows:

The results array should be considered as an array of vectors each of which is stored in 3 successive locations in the array. For example, if 6 results are required then the results array is 18 doubles long.
The nu , nv and triang specify the derivatives required, and their positions in the results array as follows:

If triang is FGEVSQ. In this case a rectangular array of derivatives is required. nu specifies the highest derivative of form dnP/dun that is required. nv specifies the highest derivative of form dnP/dvn that is required. Other entries are according to the pattern ‘ each successive column is a higher derivative in u and each successive row is a higher derivative in v’. Thus, for example, if nu=2 , nv=1 and triang=0 then the results array looks as follows:

P dP/du d2P/du2

dP/dv d2P/dudv d3P/du2dv

These positions/derivatives are then stored in the results array in row order. For example, counting from position 0 (in Fortran add 1 to these positions):

dP/du is stored in elements 3-5 of the results array.

d2p/dudv is stored in elements 12-14 of the results array.

Finally, if a derivative is NOT available then the corresponding array elements should be returned unmodified. For example, if your evaluator cannot return d3p/du2dv in the above specification you should not modify elements 15-17 of results and return 'ifail' as FGEVIN (Evaluation incomplete)
The triang argument may only take the value FGEVTR when nu = nv. In this case the array pattern is triangular and returned in row order. For example, if nu=nv=2 and triang=1 the pattern of the results array is as follows:

P dP/du 2P/du2dP/dv d2P/dudvd2P/dv2

Thus, for example:

d2P/du2 is stored in elements 6-8 of the results array.

d2P/dv2 is stored in elements 15-17 of the results array.

[back to top]

2.3 FG module design issues

[back to top]

2.3.1 General design

In Parasolid the style of implementation used for FG is as shown in the supplied example source code and detailed in this chapter. We have found it to be a fast and straightforward interface to use. We have an advantage here in that we are generally writing FG evaluators from scratch. We have designed the FG interface to be as compatible as possible with other FG systems that we have encountered as well as being already specified in a form that allows us to increase the range of curve and surface types that are implementable as FG.

[back to top]

2.3.2 Performance issues

Parasolid does not replace users’ evaluators with internal approximations: it must always request spatial information regarding external curves and surfaces by calling FGEVCU and FGEVSU respectively in order to model exactly. Therefore it is essential that the user codes these functions as efficiently as possible since any delay in returning information to Parasolid is directly reflected in the speed of modeling using FG.

[back to top]

2.3.3 Data usage issues

Data available to the FG developer

A simple evaluator may be designed to generate a single specific curve or surface. In this case no information other than parameter positions is required by the evaluator in order for it to be able to supply positions and derivatives.

However, we imagine that developers will more typically choose to write general purpose evaluators capable of generating whole families of curves or surfaces. In these cases the evaluators will require additional data to specify the particular example required.

Parasolid provides two distinct means to supply this sort of data to evaluators as arguments to the function which specifies the required curve or surface or from data supplied by the FG module when the curve or surface is initialized.

Data passed to the interface

The interface allows the user to supply an array of real numbers and/or an array of integers to the evaluator. In most cases this is the preferred method of supplying data:

This data is stored in transmit files of Parasolid bodies, so that such files are sufficient to exchange models between sites with the required evaluators linked to Parasolid.
This data must be in the form of reals or integers - as attempts to cast character strings into elements of the real array creates difficulties in generating transmit files.

Data passed to the FG module

The interface additionally allows the user to specify an area of memory which is filled by the FG module call which requests that the FG item specified by the interface call be initialized. This data :

Is not stored on any file generated by Parasolid. It therefore provides a means by which users can implement evaluators where security considerations require that no associated data be accessible from transmit files or snapshots.
Is simply stored by Parasolid and made available to the evaluator. Therefore any form of data, such as pointers or character strings, can be cast into this area.
Requires that the source of this data, such as files or databases, be available on all sites where this form of evaluator is to be used.

There is one specific use of such data which is inherent in the design of the FG interface. All evaluation requests leave Parasolid as calls to functions FGEVCU or FGEVSU. These functions therefore need to be able to route these requests to the appropriate evaluator function.

It would be possible to design these functions to switch to evaluators based upon the key supplied to the interface. However, performance considerations indicate that this is a very inefficient mechanism, particularly if many evaluators are linked into Parasolid. The interface therefore requires that at least space for one double is requested. This first element of the Frustrum array is intended to be used to implement this switch between evaluators.

In the example discussed below the address of the evaluator function is stored. This is an efficient method of implementing this switch in C but other methods such as a stored integer used in a Fortran computed GOTO statement are equally valid.

[back to top]

2.3.4 Key format for evaluator selection

There is no format which is enforced for keys by Parasolid. However, we believe that the opportunities that the FG facilities create for extending the geometrical repertoire of Parasolid may find widespread applications. We need to provide support facilities for users of such geometry that meet Parasolid's high customer support standards. In order to do this we need to be able to identify the originators of FG evaluators. We propose a standard for keys as follows:

key = <company_identifier> / <evaluator_name> / <data_source>

So for example :

Only evaluators which use the fg_data route for input need to use the <data_source> component
our corrugated surface has key EDS/corrugated
A Coons surface evaluator written by company ABC which uses secure data from a file Example_data would have key ABC/Coons/Example_data

[back to top]

2.3.5 Deletion of evaluators

The Foreign Geometry interface comprises six functions:

FGCRSU, FGCRCU to initialize curves and surfaces
FGPRCU, FGPRSU to return their parametric properties
FGEVCU, FGEVSU to perform evaluations

Missing from this list are functions to ‘release’ curves and surfaces that Parasolid has no further need of. The reason for this omission is that the decision as to when to release an evaluator is a complicated one since it depends on such things as copying geometry, the existence of dependent geometry and the Parasolid rollback mechanism. To attempt this would require much of the rollback mechanism to be implemented inside the Frustrum and would force all customers to rewrite their Frustrums, whether using foreign geometry or not. UGS reserves the right, however, to implement this in future releases, as this change in functionality is more generally useful.

[back to top]

2.4 Linking the FG module into Parasolid

The FG module must be linked into Parasolid to allow the user access to their curves and surfaces defined therein. The details of how to do this are machine specific but the principle is straightforward.

Command scripts are provided with the Parasolid release enabling the user to link the supplied example FG module together with Parasolid to form a customized version of KID.

[back to top]

<<< Introduction and Summary

Chapters

Modeling using Foreign Geometry >>>