Mass Properties

Contents

• 27.1 Introduction
  • 27.1.1 Received arguments
  • 27.1.2 Returned arguments
  • 27.1.3 Summary of options
• 27.2 Determining the mass
• 27.3 Calculating the periphery
• 27.4 Bounds
  • 27.4.1 Using mass properties to detect model differences
• 27.5 Single
• 27.6 Dealing with local density attributes
• 27.7 Calculating the mass properties of topologies with transformations
• 27.8 Using the alternative faceting method
  • 27.8.1 Chordal tolerance
• 27.9 Using mass properties in general bodies and assemblies
• 27.10 Identifying zero mass
• 27.11 Mass properties definitions

[back to top]

27.1 Introduction

This chapter provides information on using the function PK_TOPOL_eval_mass_props to evaluate mass and other properties such as area, volume, length, centre of gravity and moment of inertia. PK_TOPOL_eval_mass_props can calculate the mass properties of a single entity or a collection of them, if all entities in the collection are of the same type. It also uses density attributes that are attached to the entity or entities. See Chapter 95, “Attributes” for more information on attributes.

For an example of this functionality, see the code example in the C++\Code Examples\Inquiries\Model Analysis\Mass Props folder, located in example_applications in your Parasolid installation folder.

27.1.1 Received arguments

PK_TOPOL_eval_mass_props receives the following arguments:

A number of arguments are returned by the function providing information on the mass properties of the function. See Section 27.1.2, “Returned arguments” for more information.

27.1.2 Returned arguments

PK_TOPOL_eval_mass_props returns the following arguments:

27.1.3 Summary of options

PK_TOPOL_eval_mass_props contains a wide variety of options that enables you to control the result of the operation. The following table summarizes the options that are available, full details of which are given in the rest of the chapter.

mass_eq_0

[back to top]

27.2 Determining the mass

You can find a number of mass properties of an entity using the mass option. This option takes the following values:

The mass of an entity is used to find the centre of gravity, which in turn is needed to calculate the moment of inertia.The default value, PK_mass_m_of_i_c, will find the mass, amount , centre of gravity and moment of inertia for the entity.

[back to top]

27.3 Calculating the periphery

This option enables you to calculate the total amount of the boundary of the selected topologies of an entity and it takes the following values:

For general bodies, only the periphery of entities with a face or a solid region (i.e. dimension two and three) can be calculated. For regions, faces and edges, the periphery is calculated as the sum of the peripheries of each individual topology. Figure 27-1 shows the periphery of two adjoining faces of a unit cube. For these two faces the periphery is calculated to be 8 times the length of an edge in these two faces.

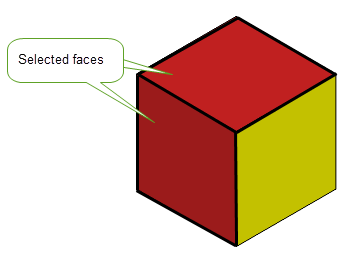
Figure 27-1 Calculating the periphery of two selected faces.

[back to top]

27.4 Bounds

You can request error bounds information using the bounds option.This option takes the following values:

It is strongly recommended that you request error bound information when calculating mass properties. The error bounds provide a very valuable indicator as to the level of accuracy of the calculated values.

27.4.1 Using mass properties to detect model differences

When comparing mass property calculations for identical or similar bodies within or across Parasolid versions, it is essential that the application requests and stores error bounds along with the calculated amount . When comparing the amount returned by two different versions of the software it is essential that the error bounds are taken into account in such comparisons. For an identical model it should always be the case that the ranges given by the amount +/- error bounds overlap, but it should not be considered a difference if the amount from version X does not lie within the range from version X+1 or vice versa.

[back to top]

27.5 Single

The single option of PK_TOPOL_eval_mass_props enables you to treat an array of faces or sheet bodies as a single solid body which can then be used to calculate the required mass properties, with the exception of its mass. Density attributes that are attached to faces or edges are ignored and the moment of inertia is calculated with an assumed density of 1. This option also allows you to calculate the mass properties of a set of an array of unsewn sheets (which when sewn would form a closed volume) as if they were sewn together to form a single body.

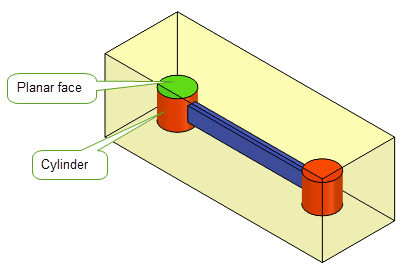
Figure 27-2 Body with a complex void

Figure 27-2 shows a block with a complex void. To calculate the negative volume of the void, the four faces of the inner cuboid and the six faces of the cylinders are supplied along with the single option. To calculate the approximate volume of one of the cylindrical voids, you need to supply the main face and the two planar faces of the cylinder along with the single option. Using the single option in this way, the cylinder will be treated as a single solid entity for the calculations.

[back to top]

27.6 Dealing with local density attributes

In Parasolid, density attributes that are attached to regions, faces, edges or vertices are referred to as local densities. See Chapter 95, “Attributes” for more information on how attributes are used in Parasolid. As the name suggests, local densities can be used on specific local topologies to selectively alter the interpretation of the global body density in that area. For example, you may want to let every face but one in a body have a certain density, and a higher density on a specific face. This can be achieved by attaching a body density to the part and a face density to the specified face. The effect of local densities on mass properties calculations is controlled by the options same_dim_density and lower_dim_density .

The values for both of these options are:

Figure 27-3 and its accompanying table shows the expectant mass of a cube of unit length sides when using these values. The body has a total body density of 7.0 attached to the body itself and a region density of 2.0 attached to the solid region inside the body. The volume of the body is 1.0.

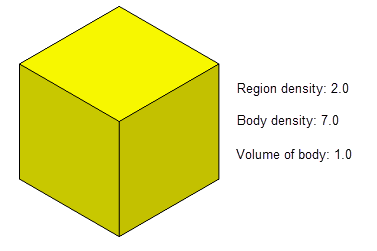
Figure 27-3 Resultant Mass values using the same_dim_density option

Figure 27-4 and its accompanying table shows the expected mass of a cube of unit length sides when using lower_dim_density . The body has a body density of 7.0, an edge density of 1.0 and two face density attributes of 3.0 and 5.0. The volume of the body is 1.0.

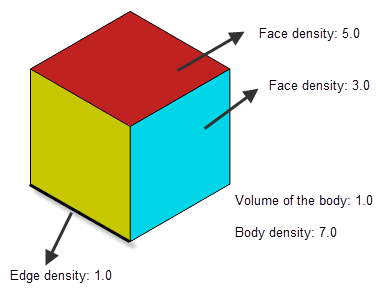
Figure 27-4 Resultant Mass values using the lower_dim_density option

[back to top]

27.7 Calculating the mass properties of topologies with transformations

You can use the transfs option to calculate the mass properties of topologies with rigid transformations and reflection transformations. This option takes an array (of size n_transfs ) of transformations that are applied to the topologies supplied in topols .

[back to top]

27.8 Using the alternative faceting method

The use_facet option of PK_TOPOL_eval_mass_props is an alternative method that is primarily provided for the purposes of debugging when validating the results produced by the main parameter-space method. It is recommended that you use the default method instead of this faceting method, especially for complex models. No error bounds are returned with this method.

With this option, a triangular facet mesh for each face referenced is generated, calculations are made on each facet and the results for all the facets are combined. The more facets you use, the more accurate the calculations will be. Figure 27-5 and Figure 27-6 illustrates using the faceting method with coarser facets and finer facets.You can also use the facet_tol option with this option. See Section 27.8.1, “Chordal tolerance” for more information on this.

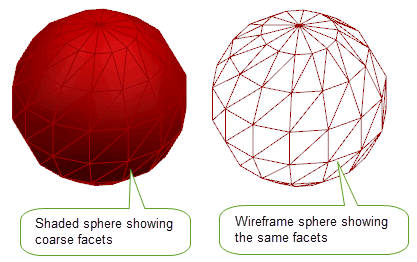
Figure 27-5 Calculating the volume of a sphere using the faceting method

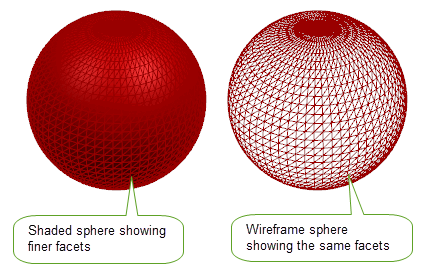
Figure 27-6 Calculating the volume of a sphere with finer facets

27.8.1 Chordal tolerance

The facet_tol option allows you to supply the chordal tolerance for facets used in conjunction with the use_facet option. Setting this option gives you control over the facets used in the alternative faceting method.

This option is equivalent to the curve_chord_tol and surface_plane_tol as used by PK_TOPOL_facet_2.

[back to top]

27.9 Using mass properties in general bodies and assemblies

Mass properties can also be calculated for general bodies and assemblies. The following table lists these as follows;

For assemblies, all body occurrences in the assembly and sub-assemblies are taken into account for the calculations. These occurrences must be of the same body type. For information on assemblies See Chapter 22, “Assemblies And Instances”.

[back to top]

27.10 Identifying zero mass

You can use the mass_eq_0 option to control the behaviour when at least one of the supplied topologies has zero mass and amount. This option takes the following values:

For information about the Parasolid Report mechanism, see Chapter 11, “Using Reports”

[back to top]

27.11 Mass properties definitions

Parasolid uses specific definitions for mass properties. These are as follows;

Mass is defined as the integral of the product of a body’s density and its amount when density is constant. The amount represents the quantity of matter in a body, which varies depending on the type of topological entity. For example, for a solid body the amount is the volume of the entity, for a sheet the amount is the area and for a wire body the amount is length.The density is obtained from the attached density attributes. If there is no density attribute attached, density has a default value of one. See Chapter 95, “Attributes” for more information on how attributes are used in Parasolid. Mass has the following mathematical equation;

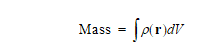
Centre of gravity is defined as the integral of the product of the density function at a given position with the position vector itself over the whole volume being considered. It has the following mathematical equation;

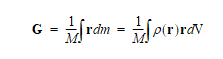
The Moment of inertia is defined as follows;

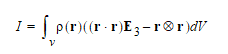
where r is the vector from the center of mass to a point in the volume v, 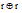is their outer product E3 is the 3X3 identity matrix and V is a region of space completely containing the object. In Parasolid, the inertia tensor matrix is defined from the moments of inertia as follows,

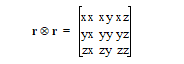
In Parasolid, the tensor returned is the moments of inertia about a point, where the point is the centre of gravity as defined in the standard Parasolid Cartesian coordinate system.

[back to top]