Parasolid View Matrices

<<< Introduction to Rendering and Faceting

Chapters

Display Tolerances >>>

Contents

• 49.1 Introduction
• 49.2 Viewing transformation
• 49.3 View matrix
  • 49.3.1 General matrix M
  • 49.3.2 Rotation submatrix R
  • 49.3.3 Perspective terms
  • 49.3.4 Array indexing

[back to top]

49.1 Introduction

Parasolid specifies the viewing data (position, direction and type) for rendering and faceting functions using a view matrix. This chapter describes the general form of such a matrix.

[back to top]

49.2 Viewing transformation

A viewing transformation is needed when:

• PK_TOPOL_render_line is used to generate silhouette and hidden line data
• PK_TOPOL_render_facet and PK_TOPOL_facet generate a view-dependent facet mesh

The view matrix referenced by the viewing transformation entity is constructed such that:

• the direction which you wish to look in is mapped onto the z axis
• your eye is at some positive value of z on the axis looking towards the origin

A perspective view is generated if the view matrix contains non-zero perspective terms.

[back to top]

49.3 View matrix

A view matrix is a PK transformation entity, which is created from a PK_TRANSF_sf_t structure containing a 4*4 homogeneous matrix. The viewing matrix M operates as a post-multiplier on row vectors containing homogenous coordinates:

[back to top]

49.3.1 General matrix M

The general matrix M consists of:

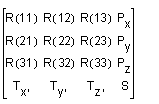
This notation is used by Newman and Sproull in one of the standard texts, "Principles of Interactive Computer Graphics" (McGraw-Hill 1973).

• R is the rotation submatrix
• the vector T represents a translation
• the vector P represents perspective
• S is the inverse global scale factor (which should be set to 1 to have no effect, but any other value except zero can be supplied to scale a view)

The support function PK_VECTOR_make_view_transf creates a suitable viewing matrix for the rendering functions which incorporates a specified view direction.

[back to top]

49.3.2 Rotation submatrix R

The rotation submatrix R defines an orthogonal set of vectors H, V and D:

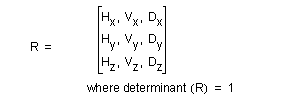
The matrix M must satisfy the following constraints:

• the rotation matrix R must be orthonormal
• the determinant on R is +1
• D and P must be parallel if P is not a zero vector
 

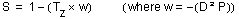
When constructing a view matrix the vector D is the negated view direction (this is because all Parasolid matrices are defined as right handed).

The other two vectors, V and H (nominally called vertical and horizontal) define the basis of the viewing coordinate system.

[back to top]

49.3.3 Perspective terms

The perspective terms Px, Py, Pz:

• can be non-zero when defining a view matrix argument for the PK rendering functions - these values determine whether the drawing is created with one, two or three point perspective or with none
• (must be zero when constructing an entity transformation matrix)

[back to top]

49.3.4 Array indexing

Parasolid requires 4*4 matrices to be defined in "column major" order.

[back to top]