Law Symbols |
|
|
|
Technical Article |
||
Description
To accept and return the nth input argument into a law, it is sometimes
specified as An, where n is an integer. The index
numbering starts at 1. For any given index number n, the argument
list has to contain at least n arguments.
Any letter of the alphabet followed by an integer n can be used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
E <> E1 !!!
O <> O1 !!!
T=T1
U=U1
X=X1
V=V2 <> V1 !!!
Y=Y2 <> Y1 !!!
Z=Z3 <> Z1 !!!
| ; law:eval A1+A2 3 4 ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate the laws. ; Use just the first input list item. (law:eval "a1+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "x+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "x1+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "t+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "t1+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "u+4" my_list) ;; 5 ; Use just the first input list item. (law:eval "u1+4" my_list) ;; 5 ; Use just the second input list item. (law:eval "a2+4" my_list) ;; 6 ; Use just the second input list item. (law:eval "b2+4" my_list) ;; 6 ; Use just the second input list item. (law:eval "y+4" my_list) ;; 6 ; Use just the second input list item. (law:eval "y2+4" my_list) ;; 6 ; Use just the second input list item. (law:eval "v+4" my_list) ;; 6 ; Use just the second input list item. (law:eval "v2+4" my_list) ;; 6 ; Use just the third input list item. (law:eval "a3+4" my_list) ;; 7 ; Use just the third input list item. (law:eval "z+4" my_list) ;; 7 ; Use just the third input list item. (law:eval "z3+4" my_list) ;; 7 ; Use just the fourth input list item. (law:eval "a4+4" my_list) ;; 8 ; Use just the fourth input list item. (law:eval "z4+4" my_list) ;; 8 ; Evaluate implied multiplication (define my_law (law a1b2c3d4e5f6Z7)) ;; my_law ; my_law => #[law A1*B2*C3*D4*E5*F6*Z7] (law:eval my_law my_list) ;; 5040 |
[Top]
| ; law "ABS(x)" ; Create a simple law. (define my_law (law "abs(x)")) ;; my_law ; => #[law "ABS(X)"] (law:eval my_law -2) ;; 2 |
[Top]
| ; law "AND" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "(x>3) and (y<2)")) ;; my_cond (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0 3) ;; 0 (law:eval 4 1) ;; 4 (law:eval 4 3) ;; 4 (law:eval 2 1) ;; 2 |
[Top]
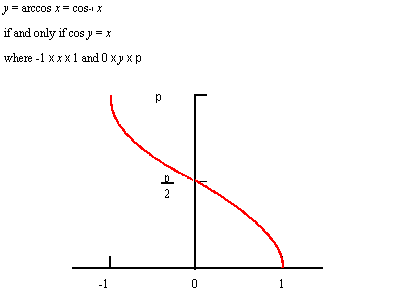
Description
The mathematical definition is:

| ; law "ARCCOS(x)" ; Define a law and take its derivative. (define f (law "arccos(x)")) ;; f ; => #[law "ARCCOS(X)"] (define df (law:derivative f)) ;; df ; => #[law "-((1-X^2)^-0.5)"] |
[Top]
Description
The mathematical definition is:
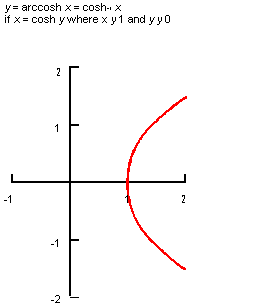
| ; law "ARCCOSH(x)" ; Define a law and take its derivative. (define f (law "arccosh(x)")) ;; f ; => #[law "ARCCOSH(X)"] (define df (law:derivative f)) ;; df ; => #[law "(-1+X^2)^-0.5"] |
[Top]
Description
The mathematical definition is:
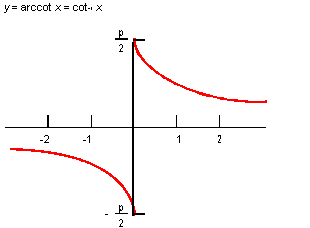
| ; law "ARCCOT(x)" ; Define a law and take its derivative. (define f (law "arccot(x)")) ;; f (define df (law:derivative f)) ;; df |
[Top]
Description
The mathematical definition is:
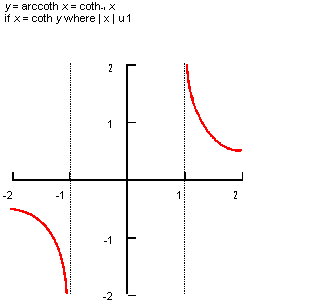
| ; law "ARCCOTH(x)" ; Define a law and take its derivative. (define f (law "arccoth(x)")) ;; f ; => #[law "ARCCOTH(X)"] (define df (law:derivative f)) ;; df ; => #[law "(1-X^2)^-1"] |
[Top]
Description
The mathematical definition is:
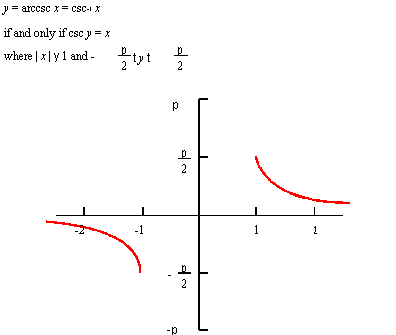
| ; law "ARCCSC(x)" ; Define a law and take its derivative. (define f (law "arccsc(x)")) ;; f ; => #[law "ARCCSC(X)"] (define df (law:derivative f)) ;; df ; => #[law "-(X^-1*(-1+X^2)^-0.5)"] |
[Top]
Description
The mathematical definition is:
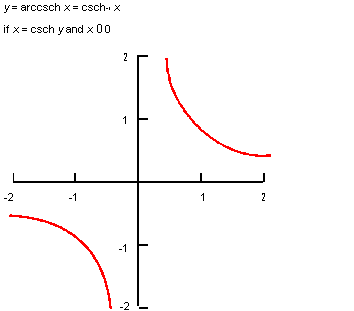
| ; law "ARCCSCH(x)" ; Define a law and take its derivative. (define f (law "arccsch(x)")) ;; f ; => #[law "ARCCSCH(X)"] (define df (law:derivative f)) ;; df ; => #[law "-(ABS(X)^-1*(1+X^2)^-0.5)"] |
[Top]
Description
The mathematical definition is:
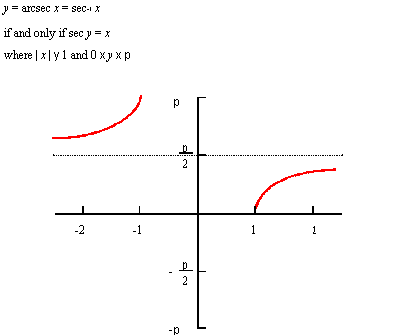
| ; law "ARCSEC(x)" ; Define a law and take its derivative. (define f (law "arcsec(x)")) ;; f ; => #[law "ARCSEC(X)"] (define df (law:derivative f)) ;; df ; => #[law "X^-1*(-1+X^2)^-0.5"] |
[Top]
Description
The mathematical definition is:
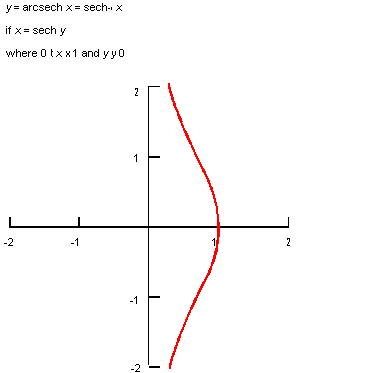
| ; law "ARCSECH(x)" ; Define a law and take its derivative. (define f (law "arcsech(x)")) ;; f ; => #[law "ARCSECH(X)"] (define df (law:derivative f)) ;; df ; => #[law "-(X^-1*(1-X^2)^-0.5)"] |
[Top]
Description
The mathematical definition is:
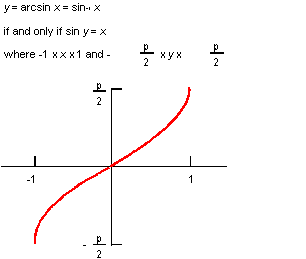
| ; law "ARCSIN(x)" ; Define a law and take its derivative. (define f (law "arcsin(x)")) ;; f ; => #[law "ARCSIN(X)"] (define df (law:derivative f)) ;; df ; => #[law "(1-X^2)^-0.5"] |
[Top]
Description
The mathematical definition is:
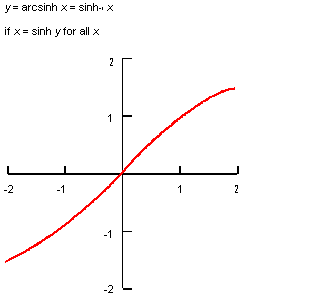
| ; law "ARCSINH(x)" ; Define a law and take its derivative. (define f (law "arcsinh(x)")) ;; f ; => #[law "ARCSINH(X)"] (define df (law:derivative f)) ;; df ; => #[law "(1+X^2)^-0.5"] |
[Top]
Description
The mathematical definition is:
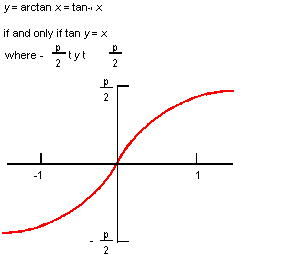
y = arctan x = tan-1
x
if and only if tan y = x
where -pi/2 < y < pi/2
| ; law "ARCTAN(x)" ; Define a law and take its derivative. (define f (law "arctan(x)")) ;; f ; => #[law "ARCTAN(X)"] (define df (law:derivative f)) ;; df ; => #[law "(1+X^2)^-1"] |
[Top]
Description
The mathematical definition is:
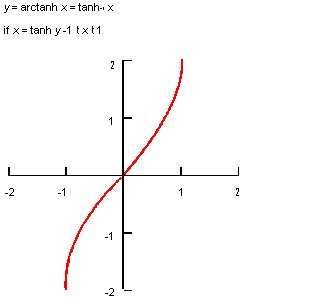
| ; law "ARCTANH(x)" ; Define a law and take its derivative. (define f (law "arctanh(x)")) ;; f ; => #[law "ARCTANH(X)"] (define df (law:derivative f)) ;; df ; => #[law "(1-X^2)^-1"] |
[Top]
Description
The variables to this law function are laws. However, my_pos, my_axis,
and my_direction have to return three elements [i.e., VEC(0, 0, 0)], while
my_distance has to return one element.
| ; law "BEND" ; Uses the BEND law symbol (define my_block (solid:block (position 0 0 0) (position 10 10 10))) ;; my_block ; my_block => #[entity 1 1] (define my_b1 (solid:block (position 0 0 0) (position 2 2 -2))) ;; my_b1 (define my_b2 (solid:block (position 0 0 0) (position 6 2 -2))) ;; my_b2 (define my_b3 (solid:block (position 0 0 0) (position 10 2 -2))) ;; my_b3 (solid:unite my_block my_b1) ;; #[entity 1 1] (solid:unite my_block my_b2) ;; #[entity 1 1] (solid:unite my_block my_b3) ;; #[entity 1 1] (define my_law (law "bend( law1, law2, law3, law4)" (position 0 0 20) (gvector 0 1 0) (gvector 0 0 1) 10)) ;; my_law ; Alternate method of specifying the same thing (define my_law2 (law "bend(vec(0,0,20),vec(0,1,0),vec(0,0,1),10)")) ;; my_law2 (law:warp my_block my_law) ;; #[entity 1 1] |
[Top]
Description
This law takes in 2 values and returns 3.
| ; law "BS" ; No example available |
[Top]
Description
The character # should not appear in the creation of a law. Instead, the
character # is meant to symbolize that any valid integer or real number
can be used as a constant. Whenever a number alone is given as a law as
input to an operation, such as
wire-body:offset,
it does not need to be enclosed in quotation marks. It is assumed to be
a law.
| ; law <#> ; Create a wire-body by offsetting a wire by ; a given distance. ; Create edge 1. (define my_edge (edge:circular (position 0 0 0) 30)) ;; my_edge ; => #[entity 2 1] (define my_wirebody (wire-body my_edge)) ;; my_wirebody ; => #[entity 3 1] ; Offset a wire-body outside the original wire-body. (wire-body:offset my_wirebody 5) ;; #[entity 4 1] ; Offset the wire-body inside the original wire-body. (wire-body:offset my_wirebody -7.5) ;; #[entity 5 1] |
[Top]
Description
The mathematical definition is:
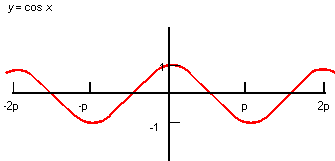
| ; law "COS(x)" ; Define a law and take its derivative. (define f (law "cos(x)")) ;; f ; => #[law "COS(X)"] (define df (law:derivative f)) ;; df ; => #[law "-SIN(X)"] |
[Top]
Description
The mathematical definition is:
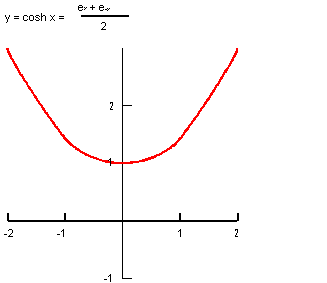
| ; law "COSH(x)" ; Define a law and take its derivative. (define f (law "cosh(x)")) ;; f ; => #[law "COSH(X)"] (define df (law:derivative f)) ;; df |
[Top]
Description
The mathematical definition is:
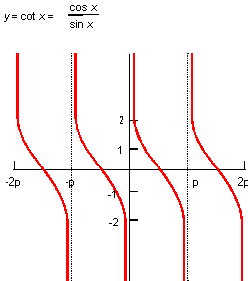
| ; law "COT(x)" ; Define a law and take its derivative. (define f (law "cot(x)")) ;; f ; => #[law "COT(X)"] (define df (law:derivative f)) ;; df |
[Top]
Description
The mathematical definition is:
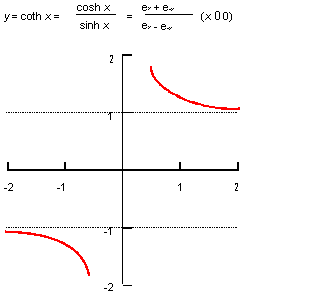
| ; law "COTH(x)" ; Define a law and take its derivative. (define f (law "coth(x)")) ;; f ; => #[law "COTH(X)"] (define df (law:derivative f)) ;; df |
[Top]
Description
The two sub-laws should return three values each.
| ; law "CROSS(law1, law2)" ; Create two gvectors. (define g1 (law (gvector 1 1 0))) ;; g1 ; => #[law "VEC(1,1,0)"] (define g2 (law (gvector 0 0 1))) ;; g2 ; => #[law "VEC(0,0,1)"] (define my_law (law "cross(law1, law2)" g1 g2)) ;; my_law ; => "cross(law1, law2)" (law:eval-vector my_law) ;; #[gvector 1 -1 0] (law:eval my_law) ;; (1 -1 0) ; Another example. ; Create a vec law. (define my_vec (law "vec( x^2, 2*x^3, x+1)")) ;; my_vec ; => #[law "VEC(X^2,2*X^3,X+1)"] ; Create another vector with two input arguments. (define my_vec2 (law "vec(x+y, y^2, X^2)")) ;; my_vec2 ; => #[law "VEC(X+Y,Y^2,X^2)"] ; Create the cross product. (define my_cross (law "cross(law1, law2)" my_vec my_vec2)) ;; my_cross ; my_cross => #[law ; "CROSS(VEC(X^2,2*X^3,X+1),VEC(X+Y,Y^2,X^2))"] ; Evaluate the law at a value of x and y. (law:eval-vector my_cross (list 2 1)) ;; #[gvector 61 -7 -44] |
[Top]
Description
The mathematical definition is:
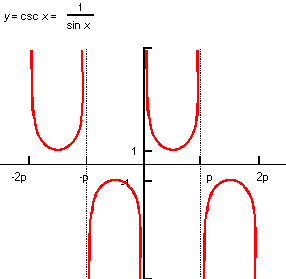
| ; law "CSC(x)" ; Define a law and take its derivative. (define f (law "csc(x)")) ;; f ; => #[law "CSC(X)"] (define df (law:derivative f)) ;; df ; => #[law "-X"] |
[Top]
Description
The mathematical definition is:
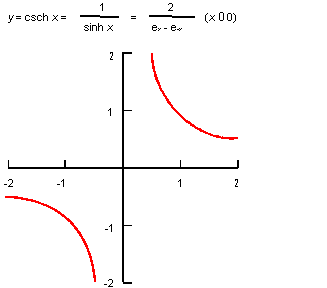
| ; law "CSCH(x)" ; Define a law and take its derivative. (define f (law "csch(x)")) ;; f ; => #[law "CSCH(X)"] (define df (law:derivative f)) ;; df ; => #[law "-(CSCH(X)*COTH(X))"] |
[Top]
Description
CUR returns the positions of the defining curve at the parameter value.
In other words, this symbol is a way to pass in an edge into a law for
other purposes, such as evaluation. The dimension of the input, my_curve_law_data,
is one, but when cur is evaluated, it returns an item in three dimensions.
| ; law "CUR(edge1)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ;; my_edge ; => #[entity 2 1] ; Input this edge into a law. (define my_law (law "cur(edge1)" my_edge)) ;; my_law ; => #[law "CUR(EDGE1)"] ; Evaluate this law at a ; parameter value. (law:eval-position my_law 2) ;; #[position -8.32293673094285 18.1859485365136 0] |
[Top]
Description
CURC returns the curvature of the defining curve at the parameter value.
This symbol operates only on sublaws, not on law data items. The dimension
of the input, my_law, is one. When CURC is evaluated, it returns a one
dimensional item.
Unlike the cur and wire laws, the CURC law symbol operations on laws and not on law data. Therefore, my_law must be a law that returns 3 values, as is the case for cur and wire law symbols.
ACIS defines its own parameter range for a curve which is not necessary the range [0,1]. If it should be defined over the range [0,1], use the map law symbol. The reciprocal of curvature is the radius of curvature.
| ; law "CURC(edge1)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 10)) ;; my_edge ; => #[entity 2 1] ; Input this edge into a law. (define my_law (law "curc(edge1)" my_edge) ;; my_law ; => #[law "CURC(EDGE1)"] ; Find the curvature at a parameter value. (law:eval my_law 0) ;; 0.1 ; Note that the curvature of the curve is the ; reciprocal of the radius of curvature. |
[Top]
Description
This finds the parameter point on a curve (my_curve_law_data) that is the
closest the given point (my_position_law). The my_position_law is typically
given as a vec law such as vec( x, y, z). The my_parameter_guess argument
is useful to localize the calculations and speed up the computation.
| ; law "CURVEPERP(x)" ; Create the points for a test curve. (define my_plist (list (position 0 0 0) (position 20 20 20) (position -20 20 20))) ;; my_plist (define my_start (gvector 1 1 1)) ;; my_start ; => #[gvector 1 1 1] (define my_end (gvector 1 1 1)) ;; my_end ; => #[gvector 1 1 1] (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; => #[entity 2 1] (define my_position_law (law (position 0 10 15))) ;; my_position_law ; => #[law "VEC(0, 10, 15)"] (define my_law (law "curveperp (edge1,law1)" my_testcur my_position_law)) ;; my_law ; => #[law "CURVEPERP (EDGE1, VEC(0,10,15))"] (law:eval my_law) ;; 52.0986698601117 |
[Top]
Description
my_law specifies which law to take the derivative of. my_variable specifies
what to take the derivative with respect to. n specifies how many derivatives
to take. Only use this law symbol for derivatives that do not have exact
derivatives. This returns the numerical derivative of the my_law.
When D is followed by a parenthesis, it means the derivative. When it
is followed by an integer n, it implies an input argument and not
the derivative.
D() <> Dn !!!
T=U=X=A1=B1=...=D1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=D2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=D3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Dn=...=Zn.
| ; law "D( law1), x, 1)" ; Create a simple law. (define my_law (law "d(cos(x), x, 1)")) ;; my_law ; => #[law "D(COS(X),X,1)"] (law:eval my_law 2) ;; -0.909297426824329 (law:eval my_law 3) ;; -0.141120008059955 |
[Top]
Description
my_curve_law_data is the curve used as input to the derivative operation.
num specifies the number of derivatives to take of the curve. This is
the same as cur except that it takes a second argument, num, for the number
of derivatives. When num is 0, the result is the same as cur. This law
symbol returns parametric derivatives as opposed to geometric derivatives.
| ; law "DCUR(edge1, 1)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ;; my_edge ; => #[entity 2 1] ; Input this edge into a law ; which takes its derivative. (define my_law (law "dcur(edge1,1)" my_edge)) ;; my_law ; => #[law "DCUR(EDGE1,1)"] ; Evaluate this derivative function of the edge ; at a parameter value. (law:eval-vector my_law 2) ;; #[gvector -18.1859485365136 -8.32293673094285 0] (law:eval-vector my_law 0) ;; #[gvector 0 20 0] |
[Top]
Description
Parsing actually involves the / character. my_law1 and my_law2 can be any
valid law. my_law1 can have more than one dimension, but my_law2 has to
be one dimensional.
| ; law "/" ; Create a simple law. (define my_firstlaw (law "x^2")) ;; my_firstlaw ; => #[law "X^2"] ; Create a second simple law. (define my_secondlaw (law "x*3")) ;; my_secondlaw ; => #[law "x*3"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law2/2*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ; => #[law "X*3/2*X^2"] (law:eval my_complexlaw 2) ;; 12 |
[Top]
| ; law "DOMAIN(x)" ; Create a simple law function. |
[Top]
Description
The input sublaws, my_law1 and my_law2, are not restricted in their return
dimensional values. If one input law has a smaller dimension than the
other, it will be padded with zeros.
| ; law "DOT( law1, law2)" ; Create two gvectors. (define g1 (law (gvector 1 1 0))) ;; g1 ; => #[law "VEC(1,1,0)"] (define g2 (law (gvector 0 0 1))) ;; g2 ; => #[law "VEC(0,0,1)"] (define my_law (law "dot( law1, law2)" g1 g2)) ;; my_law ; => #[law "DOT(VEC(1,1,0),VEC(0,0,1))"] (law:eval my_law) ;; 0 ; Another example. ; Create a vec law. (define my_vec (law "vec( x^2, 2*x^3, x+1)")) ;; my_vec ; => #[law "VEC(X^2,2*X^3,X+1)"] ; Create another vector with two input arguments. (define my_vec2 (law "vec( x+y, y^2, X^2)")) ;; my_vec2 ; => #[law "VEC(X+Y,Y^2,X^2)"] ; Create the dot product. (define my_dot (law "dot(law1, law2)" my_vec my_vec2)) ;; my_dot => ; => #[law ; "DOT(VEC(X^2,2*X^3,X+1),VEC(X+Y,Y^2,X^2))"] ; Evaluate the law at a value of x and y. (law:eval my_dot (list 2 1)) ;; 40 |
[Top]
Description
my_curve_law_data is the pcurve used as input to the derivative operation.
num specifies the number of derivatives to take of the curve. This is
the same as pcur except that it takes a second argument, num, for the
number of derivatives. When num is 0, the result is the same as pcur.
This law symbol returns parametric derivatives as opposed to geometric
derivatives.
| ; law "DPCUR(x)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ;; my_edge ; => #[entity 2 1] ; Input this edge into a law ; which takes its derivative. (define my_law (law "dpcur(edge1,1)" my_edge)) ;; my_law ; => #[law "DCUR(EDGE1,1)"] ; Evaluate this derivative function of the pcurve ; underlying the edge at a parameter value. (law:eval my_law 2) ;; (-18.1859485365136 -8.32293673094285) (law:eval-vector my_law 0) ;; (0 20) |
[Top]
Description
my_surface_law_data is the curve used as input to the derivative operation.
num specifies the number of derivatives to take of the curve. This is
the same as surf except that it takes two more arguments. numu is the
number of derivatives to take with respect to u, and numv is the
number of derivatives to take with respect to v. When num is 0,
the result is the same as surf. This law symbol returns parametric derivatives
as opposed to geometric derivatives.
| ; law "DSURF( surf1, 1, 0)" ; Take the derivative of the surface at a point. ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; => #[entity 2 1] (define my_dsurflaw_u (law "dsurf(surf1,1,0)" (car (entity:faces my_sphere)))) ;; my_dsurflaw_u ; my_dsurflaw_u ; => #[law "DSURF(SURF1,1,0)"] (law:eval-vector my_dsurflaw_u (list 0 0)) ;; #[gvector 0 0 10] ; This is the tangent vector in the u direction. (define my_dsurflaw_v (law "dsurf(surf1,0,1)" (car (entity:faces my_sphere)))) ;; my_dsurflaw_v ; my_dsurflaw_v ; => #[law "DSURF(SURF1,0,1)"] (law:eval-vector my_dsurflaw_v (list 0 0)) ;; #[gvector 0 10 0] ; This is the tangent vector in the v direction. |
[Top]
Description
my_wire_law_data is the wire used as input to the derivative operation.
num specifies the number of derivatives to take of the curve. This is
the same as wire except that it takes a second argument, num, for the
number of derivatives. When num is 0, the result is the same as wire.
This law symbol returns a scaled parametric derivatives as opposed to
geometric derivatives.
| ; law "DWIRE( wire1, 1)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ;; my_edge ; => #[entity 2 1] ; Create a wire body from this edge. (define my_body (wire-body my_edge)) ;; my_body ; => #[entity 3 1] ; Input this wire body into a law ; which takes its derivative. (define my_law (law "dwire(wire1,1)" my_body)) ;; my_law ; => #[law "DWIRE(WIRE1,1)"] ; Evaluate this derivative function of the wire ; at a parameter value. (law:eval-vector my_law 0) ;; #[gvector 0 1 0] |
[Top]
Description
e is the base of the natural system of logarithms. It is the limit
of (1+1/n)n as n increases without limit;
it is also the sum of the infinite series 1+1/1!+1/2!+1/3!+1/4!+...; its
numerical value is 2.718281828459045....
When E is followed by an integer n, it implies an input argument
and not the base of the natural logs.
E <> En !!!
T=U=X=A1=B1=...=E1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=E2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=E3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=En=...=Zn.
| ; law "E" ; Define a law. (define my_law (law "ln( e)")) ;; my_law ; => #[law "LN(E)"] ; Evaluate the law. (law:eval my_law) ;; 1 (define my_law2 (law "e^x")) ;; my_law2 ; => #[law "E^X"] (law:eval my_law2 1) ;; 2.71828182845905 (law:eval my_law2 2) ;; 7.38905609893065 |
[Top]
Description
Some law functions, such as curc, cur, and dcur, accept curve law data
as input arguments. When working with APIs, these can be anything derived
from the curve class and bounded. When working in Scheme, however, these
should be edges.
When a bounded curve (for example, an edge) is used as input into a law, it is always followed by an integer n that specifies its index into the input argument list. The index numbering starts at 1. For any given index number n, the argument list has to contain at least n arguments.
A law expression with edge1 and law1 followed by a curve and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for example, a law and then a curve) and then specify the index number (for example, edge2 and law1).
| ; law "EDGE1" ; Define an edge from a bunch of points. (define my_plist (list (position 0 0 0) (position 20 20 0) (position 40 0 0) (position 60 25 0) (position 40 50 0) (position 20 30 0) (position 0 50 0))) ;; my_plist (define my_start (gvector 1 1 0)) ;; my_start ; => #[gvector 1 1 0] (define my_end (gvector -1 1 0)) ;; my_end ; => #[gvector -1 1 0] (define my_edge (edge:spline my_plist my_start my_end)) ;; my_edge ; => #[entity 2 1] ; Define a law and take its derivative. (define my_law (law "map (curc (edge1),edge1)" my_edge)) ;; my_law ; => #[law "MAP (CURC(EDGE1),EDGE2)"] (define my_maxpoint (law:nmax my_law 0.5 1)) ;; my_maxpoint ; => 0.840637305143896 (define my_point (dl-item:point (curve:eval-pos my_edge my_maxpoint))) ;; my_point ; => #[dl-item 22F793F0] (dl-item:display my_point) ;; () |
[Top]
| ; law "=" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x=3")) ;; my_cond (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 0 (law:eval 4) ;; 4 (law:eval 3) ;; 3 |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. Numbering of selective boolean cells starts at 0. Therefore, if
there are five cells, even? keeps 0, 2, 4... The other cells are thrown
away.
| ; law "EVEN?(x)" ; Create a sweep example to show selective booleans. (define blank (solid:block (position -10 -10 5) (position 10 10 30))) ;; blank ; blank => [entity 2 1] (define b2 (solid:block (position -5 -10 10) (position 10 10 15))) ;; b2 (define b3 (solid:block (position -5 -10 20) (position 10 10 25))) ;; b3 (solid:subtract blank b2) ;; [entity 7 1] (solid:subtract blank b3) ;; [entity 7 1] (define profile (edge:ellipse (position 0 0 0) (gvector 0 0 1)2)) ;; profile (define path (edge:linear (position 0 0 0) (position 0 0 35))) ;; path (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "even?(x)")) ;; opts (sweep:law profile path opts) ;; #[entity 7 1] |
[Top]
| ; law "EXP(x)" ; Create a simple law. (define my_law (law "exp(x)")) ;; my_law ; => #[law "EXP(X)"] (law:eval my_law 1) ;; 2.71828182845905 |
[Top]
Description
Parsing actually involves the ^ character. my_law1 and my_law2 can be any
valid law. If my_law is x and my_law2 is 3, this takes x to the third
power. Exponents take precedence over multiplication/division and addition/subtraction.
Both my_law1 and my_law2 have to be single dimension.
| ; law "^" ; Create a simple law. (define my_firstlaw (law "x^2")) ;; my_firstlaw ; => #[law "X^2"] ; Create a second simple law. (define my_secondlaw (law "x*3")) ;; my_secondlaw ; => #[law "X*3"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law2^3*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ; => #[law "(X*3)^(X^2)"] (law:eval my_complexlaw 1) ;; 27 (law:eval my_complexlaw 2) ;; 864 |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. This is a shorthand way of stating that all cells are to be kept.
This law symbol has other uses not yet exploited yet.
| ; law "FALSE" ; Create a sweep example to show selective booleans. (define blank (solid:block (position -10 -10 5) (position 10 10 30))) ;; blank ; blank => [entity 2 1] (define b2 (solid:block (position -5 -10 10) (position 10 10 15))) ;; b2 (define b3 (solid:block (position -5 -10 20) (position 10 10 25))) ;; b3 (solid:subtract blank b2) ;; [entity 2 1] (solid:subtract blank b3) ;; [entity 2 1] (define profile (edge:ellipse (position 0 0 0) (gvector 0 0 1)2)) ;; profile (define path (edge:linear (position 0 0 0) (position 0 0 35))) ;; path (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "TRUE")) ;; opts (sweep:law profile path opts) ;;[entity 2 1] ; Attempt sweep again without keeping anything. (roll) ;; -1 (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "FALSE")) ;; opts (sweep:law profile path opts) ;; #[entity 2 1] |
[Top]
Description
Returns second geometric derivative of its sublaw, my_law. This is a vector
pointing in the direction of the direction of curvature. The geometric
derivative is the derivative of the curve parameterized with respect to
the arc length.
This law symbol is used to specify the orientation of a surface by defining a vector fields along a curve. This defines rails which help orient a surface when performing sweep operations.
| ; law "FRENET" ; Produces a frenet rail law. (define my_line (edge:linear (position 0 0 0) (position 0 (law:eval "8*pi") 0))) ;; my_line ; my_line => #[entity 2 1] (define my_wire (wire-body my_line)) ;; my_wire ; my_wire => #[entity 3 1] (define my_helix (wire-body:offset my_wire 5 "x")) ;; my_helix ; my_helix => #[entity 4 1] (define my_path (law "cur(edge1)" (car (entity:edges my_helix)))) ;; my_path ; my_path => #[law "CUR(EDGE1)"] (define my_frenet (law "map(frenet(law1),edge2)" my_path(car (entity:edges my_helix)))) ;; my_frenet ; my_frenet => #[law "MAP(FRENET(CUR(EDGE1)),EDGE2"] ; This maps my_frenet laws domain to the closed ; interval [0,1]. (law:hedgehog my_frenet my_helix 50) ;; #[dl-item 40261f30] |
[Top]
Description
The Gaussian curvature is the result of multiplying the two principal curvatures
at the point on the surface. This law takes in 2 values and returns 1.
| ; law "GAUSCUR" ; No example available |
[Top]
| ; law ">" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x>3")) ;; my_cond (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 0 (law:eval 4) ;; 4 (law:eval 3) ;; 3 |
[Top]
| ; law ">=" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x>=3")) ;; my_cond (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 0 (law:eval 4) ;; 4 (law:eval 3) ;; 3 |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. This law symbol is used to test if something is an integer. It can
be used with other law operations.
| ; law "INT?(x)" ; Create a simple law. |
[Top]
Description
The LAW
class derives from ENTITY,
so it has the properties
of an ENTITY, such as save
and restore. It uses the same construction and destruction as a standard
ENTITY. To create a new law,
an application may do the following:
law *law_to_be_used = ...; // create
a law
LAW *law_entity=ACIS_NEW LAW(law_to_be_used);
Law can also be used to check for SAT file problems concerning laws, as in the following example.
| ; law "LAW" ; Check for law-related SAT file problems. (define law_out (law "vec(x^2,cos(x)+arctan(y))")) ;; law_out (define law_ent (law:make-entity law_out)) ;; law_ent (part:save `d:/tmp/law_ent.sat) ;; #t (part:clear) ;; #t (define law_in (car (part:load `d:/tmp/law_ent.sat))) ;; law_in (entity:check law_in) ;; #f |
[Top]
Description
Nearly all law functions accept laws as input arguments. A law can be a
simple identity law (for example, x, y, z, xn), a more complex
law, gvectors, or positions. Accepting law functions as input into other
law functions permits more complex laws to be created.
When a law is used as input into a law, it is always followed by an integer n that specifies its index into the input argument list. The index numbering starts at 1. For any given index number n, the argument list has to contain at least n arguments.
A law expression with edge1 and law1 followed by a curve and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for example, a law and then a curve) and then specify the index number (for example, edge2 and law1).
| ; law "LAW1" ; Create a simple law function. (define my_firstlaw (law "x^2")) ;; my_firstlaw ; fine my_firstlaw (law "x^2")) ; my_firstlaw => #[law "X^2"] ; Create a second simple law function. (define my_secondlaw (law "Y")) ;; my_secondlaw ; my_secondlaw => #[law "Y"] ; Create a third law function that takes two ; laws as input arguments. (define my_complexlaw (law "law2+3*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ; my_complexlaw => #[law "Y+3*X^2"] ; Create another example with law as an input. (define my_edge (edge:circular (position 0 0 0) 30 0 90)) ;; my_edge ; my_edge => #[entity 2 1] ; my_edge is the first input argument, edge1. ; my_law is the second input argument, law2. (define my_newlaw (law "curC(edge1)+law2" my_edge my_firstlaw)) ;; my_newlaw ; my_newlaw => #[law "CURC(EDGE1)+X^2)"] |
[Top]
| ; law "length_param" ; No example availabe |
[Top]
| ; law "<" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x<3")) ;; my_law (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 1 (law:eval 4) ;; 0 (law:eval 3) ;; 0 |
[Top]
| ; law "<=" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x<=3")) ;; my_law (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 1 (law:eval 4) ;; 0 (law:eval 3) ;; 1 |
[Top]
| ; law "LN(x)" ; Create a simple law. (define my_law (law "ln(x)")) ;; my_law ; my_law => #[law "LN(X)"] (law:eval my_law 2.71828) ;; 0.999999327347282 |
[Top]
Description
This Makes a law that takes the log to a given my_base of the given my_law.
If no my_base is specified, this assumes log to the base 10.
| ; law "LOG(x)" ; Create a simple law. (define my_law (law "log(x, 2)")) ;; my_law ; => #[law "LOG(X,2)"] (law:eval my_law 3) ;; 1.58496250072116 |
[Top]
Description
For a given set of input variables, this law symbol evaluates its included
law symbols. For example, my_law1, my_law2, and my_lawn returns the largest
value from all included functions. All sublaws must return one value.
| ; law "MAX( law1, law2)" ; Create a simple law. (define my_law (law "log(x)")) ;; my_law ; => #[law "LOG(X,10)"] (law:eval my_law 10) ;; 1 ; law ln ; Create a simple law. (define my_law2 (law "ln(x)")) ;; my_law2 ; => #[law "LN(X)"] (law:eval my_law 10) ;; 1 ; Use the maximum of the two laws. (define my_max (law "max(law1, law2)" my_law my_law2)) ;; my_max ; => #[law "MAX(LOG(X,10),LN(X))"] (law:eval my_max 10) ;; 2.30258509299405 (law:eval my_max 5) ;; 1.6094379124341 |
[Top]
Description
This law takes in 2 values and returns 1.
| ; law "MAXCUR" ; Example not available |
[Top]
Description
The mean curvature is the average of the two principal curvatures at the
point on the surface. This law takes in 2 values and returns 1.
| ; law "MEANCUR" ; Example not available |
[Top]
Description
For a given set of input variables, this law symbol evaluates its included
law symbols, my_law1, my_law2, my_lawn, and returns the smallest
value from all included functions. All sublaws must return one value.
| ; law "MIN( law1, law2)" ; Create a simple law. (define my_law (law "log(x)")) ;; my_law ; => #[law "LOG(X,10)"] (law:eval my_law 10) ;; 1 ; law "ln" ; Create a simple law. (define my_law2 (law "ln(x)")) ;; my_law2 ; => #[law "LN(X)"] (law:eval my_law 10) ;; 1 ; Use the maximum of the two laws. (define my_max (law "min(law1, law2)" my_law my_law2)) ;; my_max ; => #[law "MAX(LOG(X,10),LN(X))"] (law:eval my_max 10) ;; 1 (law:eval my_max 5) ;; 0.698970004336019 |
[Top]
Description
This law takes in 2 values and returns 1.
| ; law "MINCUR" ; Example not available |
[Top]
Description
This law function returns a vector field. my_path is an edge or a wire.
my_vector is the starting direction vector. The other vectors along my_path
are determined by a minimal adjustment from the previous vector. The result
is a vector field on my_path starting at my_vector, which has minimal
rotation about my_path. This law obtains as little twist as possible.
This law function is used to specify the orientation of a surface by defining a vector fields along a curve. This defines rails which help orient a surface when performing sweep operations.
| ; law "MINROT( law1)" ; Produces a minimum rotation rail law. (define my_plist (list (position 0 0 0) (position 10 0 0) (position 10 10 0) (position 10 10 10))) ;; my_plist (define my_start (gvector 1 0 0)) ;; my_start (define my_end (gvector 0 0 1)) ;; my_end (define my_curve (edge:spline my_plist my_start my_end)) ;; my_curve (define my_path (law "cur(edge1)" my_curve)) ;; my_path ; => #[law "CUR(EDGE1)"] (define my_minrot (law "minrot(law1)" my_path)) ;; my_minrot ; my_minrot => #[law "MINROT(CUR(EDGE1))"] (law:hedgehog my_minrot my_curve 50) ;; () |
[Top]
Description
Parsing actually involves the - character. my_law1 and my_law2 can be any
valid law. Both my_law1 and my_law2 can be multiple dimensions; the smaller
of the two is padded with zeros.
| ; law "-" ; Create a simple law. (define my_firstlaw (law "x^2")) ;; my_firstlaw ; => #[law "X^2"] ; Create a second simple law. (define my_secondlaw (law "x*3")) ;; my_secondlaw ; => #[law "X*3"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law2-3*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ;; => #[law "X*3-3*X^2"] (law:eval my_complexlaw 2) ;; -6 |
[Top]
Description
Parsing actually involves the - character. my_law1 can be any valid law.
| ; law "-" ; Create a simple law ; Show the negation operation. (law:eval "-x*3" 3) ;; -9 |
[Top]
Description
This law symbol normalizes the length of my_law to be of unit length. This
is accomplished by dividing each dimension element by the square root
of the sum of the squares of all of the return elements. This is applicable
to a law that returns any dimension.
| ; law "NORM( law1)" ; Create a vec law. (define my_vec (law "vec( x^2, 2*x^3, x+1)")) ;; my_vec ; => #[law "VEC(X^2,2*X^3,X+1)"] ; Create normalized vector. (define my_norm (law "norm(law1)" my_vec)) ;; my_norm ; => #[law "NORM(VEC(X^2,2*X^3,X+1))"] ; Evaluate the normalized vector. (law:eval-vector my_norm 1) ;; #[gvector 0.333333333333333 0.666666666666667 ;; 0.666666666666667] (law:eval-position my_norm 2) ;; #[position 0.238619994508757 0.95447997803503 ;; 0.178964995881568] |
[Top]
| ; law "NOT" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "NOT(x)")) ;; my_law (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 1 (law:eval 1) ;; 0 |
[Top]
| ; law "!=" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "x!=3")) ;; my_law (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0) ;; 1 (law:eval 4) ;; 1 (law:eval 3) ;; 0 |
[Top]
Description
The law class should never be directly instantiated. Only classes derived
from law should be instantiated. Hence there is no law symbol for this
law, and calling the law::symbol
method will result in a syserror.
| ; law "NULL" ; Should never be used. |
[Top]
Description
The composition function is useful whenever complicated input expressions,
my_law2, are needed for my_law1. The output dimension of my_law2 must
be the input dimension of my_law1. The input values to my_law2 are evaluated
first, and the results are used as the input values to my_law1.
For example, lets assume we have the complicated expression for my_law:
(define my_law (x^2 + 1) / (x^2 + sqrt(x) - 4*x^3))
Now lets assume that for every value of x in the above expression, we need to substitute the my_law2 expression:
(define my_law2 (x/(2*pi) + 1))
The result, when written out by hand or typed into the computer, isnt very easy to understand.
(define my_law3 ((x/(2*pi) + 1)^2 + 1) / ((x/(2*pi) + 1)^2 + sqrt((x/(2*pi) + 1)) - 4*(x/(2*pi) + 1)^3))
Two equivalent function composition are:
(define my_law5 ((x^2 + 1) / (x^2 + sqrt(x) - 4*x^3) o (x/(2*pi) + 1))
(define my_law5 (my_law O my_law2))
When O is followed by an integer n, it implies an input argument
and not composition.
O <> On !!!
T=U=X=A1=B1=...=O1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=O2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=O3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=On=...=Zn.
| ; law "law1 O law2" ; Assume that we want a sine wave to be defined ; over the range 1 to 2 instead of 0 to 2 pi. (define my_firstlaw (law "sin(x)")) ;; my_firstlaw ; => #[law "sin(X)"] ; Create a second simple law for ; the range. (define my_secondlaw (law "x/(2*pi)+1")) ;; my_secondlaw ; => #[law "X/(2*PI)+1"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law1 o law2" my_firstlaw my_secondlaw)) ;; my_complexlaw ;; => #[law "(SIN(X))O(X/(2*PI)+1)"] (law:eval my_complexlaw 0) ;; 0.841470984807897 ; Check the results. (law:eval "sin(x/(2*pi) + 1)" 0) ;; 0.841470984807897 |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. Numbering of selective boolean cells starts at 0. Therefore, if
there are five cells, odd? keeps 1, 3, 5... The other cells are thrown
away.
| ; law "ODD?(x)" ; Create a sweep example to show selective booleans. (define blank (solid:block (position -10 -10 5) (position 10 10 30))) ;; blank ; blank => [entity 2 1] (define b2 (solid:block (position -5 -10 10) (position 10 10 15))) ;; b2 (define b3 (solid:block (position -5 -10 20) (position 10 10 25))) ;; b3 (solid:subtract blank b2) ;; [entity 2 1] (solid:subtract blank b3) ;; [entity 2 1] (define profile (edge:ellipse (position 0 0 0) (gvector 0 0 1)2)) ;; profile (define path (edge:linear (position 0 0 0) (position 0 0 35))) ;; path (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "odd?(x)")) ;; opts (sweep:law profile path opts) ;; #[entity 1 1] |
[Top]
| ; law "OR" ; Create a conditional law for later use ; by PIECEWISE (define my_cond (law "(x>3) or (y<2)")) ;; my_law (define my_law (law "piecewise(law1, law2, law3)" my_cond 1 0)) ;; my_law (law:eval 0 3) ;; 0 (law:eval 4 1) ;; 1 (law:eval 0 1) ;; 1 |
[Top]
Description
pcur returns the positions of the defining pcurve at the parameter value.
In other words, this symbol is a way to pass in a pcurve into a law for
other purposes, such as evaluation. The dimension of the input, my_pcurve_law_data,
is one, but when pcur is evaluated, it returns an item in two dimensions.
| ; law "PCUR(x)" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ;; my_edge ; => #[entity 2 1] ; Input this edge into a law. (define my_law (law "pcur(edge1)" my_edge)) ;; my_law ; => #[law "PCUR(EDGE1)"] ; Evaluate this law at a ; parameter value. (law:eval my_law 2) ;; (-8.32293673094285 18.1859485365136) |
[Top]
| ; law "PCURVE" ; Create a simple law. |
[Top]
| ; law "PDOMAIN" ; Example not available |
[Top]
Description
pi is used to denote the ratio of the circumference of a circle to
its diameter; pi is 3.1415926535898....
| ; law "PI" ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate the laws. ; Use just the first input list item. (law:eval "pi*a1^2") my_list) ;; 3.1415926535898 ; Use just the second input list item. (law:eval "pi*a2^2") my_list) ;; 12.5663706143592 |
[Top]
Description
Permits an operation to be performed in a piecewise fashion, depending
upon the conditions that were established. Both the conditions
cond1 and cond2 and the laws my_law1, my_law2, my_default_law are
normal law declarations. The number of laws in the statement has to be
one more than the number of conditions, because the last law serves as
the catchall else in the evaluation.
| ; law "PIECEWISE" ; Shows how (define my_block (solid:block (position -10 -10 -10) (position 10 10 10))) ;; my_block (define my_cylinder (solid:cylinder (position 0 0 -10) (position 0 0 10) 2)) ;; my_cylinder (define my_sub (solid:subtract my_block my_cylinder)) ;; my_sub (define my_law1 (law "vec(3*(x-3)*2,y,z)")) ;; my_law1 (define my_law2 (law "vec(-3*(x+3)*2,y,z)")) ;; my_law2 (define my_default (law "vec(x,y,z)")) ;; my_law3 (define my_cond1 (law "x>3")) ;; my_cond1 (define my_cond2 (law "x<-3")) ;; my_cond2 (define my_law (law "piecewise(law1,law2,law3,law4,law5)" my_cond1 my_law1 my_cond2 my_law2 my_default)) ;; my_law (define my_warp (law:warp my_sub my_law)) ;; my_warp |
[Top]
Description
Parsing actually involves the + character. my_law1 and my_law2 can be any
valid law. Both my_law1 and my_law2 can be multiple dimensions; the smaller
of the two is padded with zeros.
| ; law "+" ; Create a simple law. (define my_firstlaw (law "x^2")) ;; my_firstlaw => #[law "X^2"] ; Create a second simple law. (define my_secondlaw (law "x*3")) ;; my_secondlaw ; => #[law "X*3"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law2+3*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ; => #[law "X*3+3*X^2"] (law:eval my_complexlaw 2) ;; 18 |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. Numbering of selective boolean cells starts at 0. The cells which
are not prime numbers are thrown away.
| ; law "PRIME?(x)" ; Create a sweep example to show selective booleans. (define blank (solid:block (position -10 -10 5) (position 10 10 30))) ;; blank ; blank => [entity 2 1] (define b2 (solid:block (position -5 -10 10) (position 10 10 15))) ;; b2 (define b3 (solid:block (position -5 -10 20) (position 10 10 25))) ;; b3 (solid:subtract blank b2) ;; [entity 2 1] (solid:subtract blank b3) ;; [entity 2 1] (define profile (edge:ellipse (position 0 0 0) (gvector 0 0 1)2)) ;; profile (define path (edge:linear (position 0 0 0) (position 0 0 35))) ;; path (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "prime?(x)")) ;; opts (sweep:law profile path opts) ;; #[entity 1 1] |
[Top]
Description
The rotate law symbol requires that my_law return vectors. It produces
vectors that have by transformed by the my_transf. Rotate is used on vectors,
while trans is used to transform positions. If the transform input to
this law does a rotation (for example, transform:rotation) and a translation
(transform:translation),then this law only works on the rotational component.
| ; law "ROTATE(trans1)" ; Create a transform, and then create its inverse. (define my_trans_rot (transform:rotation (position 0 0 0) (gvector 1 0 0) 90)) ;; my_trans_rot ; => #[transform 1075263768] (define my_trans_move (transform:translation (gvector 1 0 0))) ;; my_trans_move ; => #[transform 1075264512] (define my_t_comp (transform:compose my_trans_rot my_trans_move)) ;; my_t_comp ; => #[transform 1075265208] (define my_law_rotate (law "rotate(vec(x,y,z),trans1)" my_t_comp)) ;; my_law_rotate ; => #[law "ROTATE(VEC(X,Y,Z),TRANS1)"] ; This transforms the given law VEC(X,Y,Z) by ; the supplied transform, my_t_comp (law:eval my_law_rotate (list 0 0 1)) ;; (0 -1 6.12323399573677e-17) ; In this example, the input vector is (0, 0, 1). ; It gets rotated by 90 degrees, causing y to be ; -1 but does NOT get moved along x axis by 1. ; z is approximately zero. (define my_law_both (law "trans(vec(x,y,z),trans1") my_t_comp)) ;; my_law_both ; => #[law "TRANS(VEC(X,Y,Z),TRANS1)"] ; This transforms the given law "VEC(X,Y,Z)" by ; the supplied transform, my_t_comp (law:eval my_law_both (list 0 0 1)) ;; (1 -1 6.12323399573677e-17) ; In this example, the input vector is (0, 0, 1). ; It gets rotated by 90 degrees, causing y to be ; -1 and then gets moved along x axis by 1. ; z is approximately zero. |
[Top]
Description
The mathematical definition is:
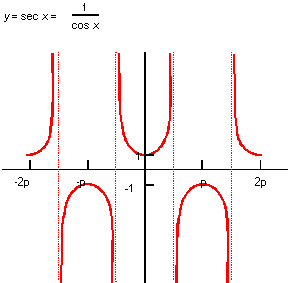
| ; law "SEC(x)" ; Define a law and take its derivative. (define f (law "sec(x)")) ;; f ; => #[law "SEC(X)"] (define df (law:derivative f)) ;; df ; => #[law "SEC(X)*TAN(X)"] |
[Top]
Description
The mathematical definition is:
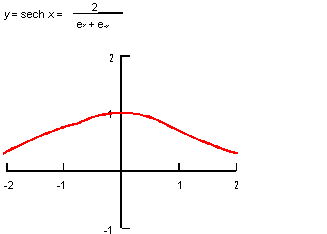
| ; law "SECH(x)" ; Define a law and take its derivative. (define f (law "sech(x)")) ;; f ; => #[law "SECH(X)"] (define df (law:derivative f)) ;; df ; => #[law "-(SECH(X)*TANH(X))"] |
[Top]
Description
The set function is used primarily to define derivatives of special functions.
If the sublaw symbol is positive, it returns a 1; if the sublaw symbol
is negative, it returns a 0.
For example, the derivative of the absolute value of x is 1 for positive values of x and -1 for negative values of x. Hence, the derivative can be expressed as set(x)-(1-set(x)).
The functions abs, max, and min all use the set function when a derivative is taken of them.
| ; law "SET" ; Create a simple law. (define my_law (law "abs(cos(x))")) ;; my_law ; => #[law "ABS(COS(X))"] ; Create a derivative law. (define my_secondlaw (law:derivative my_law)) ;; my_secondlaw ;; => #[law ;; "SET(COS(X))*-SIN(X)+(1-SET(COS(X)))*SIN(X)"] |
[Top]
Description
The mathematical definition is:
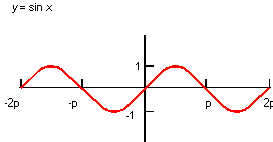
| ; law "SIN(x)" ; Define a law and take its derivative. (define f (law "sin(x)")) ;; f ; => #[law "SIN(X)"] (define df (law:derivative f)) ;; df ; => #[law "COS(X)"] |
[Top]
Description
The mathematical definition is:
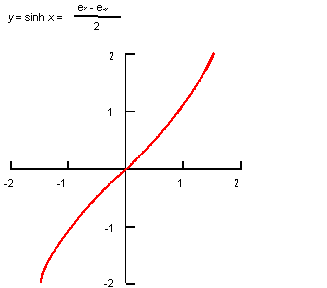
| ; law "SINH(x)" ; Define a law and take its derivative. (define f (law "sinh(x)")) ;; f ; => #[law "SINH(X)"] (define df (law:derivative f)) ;; df ; => #[law "COSH(X)"] |
[Top]
| ; law "SIZE" ; Determines the square root of the sum of the ; squares in a VEC. (define my_law (law "vec( 2, 3, 4)")) ;; my_law (define my_size (law "size(law1)" my_law)) ;; my_size (law:eval my_size 0) ;; 5.3852 |
[Top]
| ; law "SQRT" ; Create a simple law. (define my_firstlaw (law "sqrt(x)")) ;; my_firstlaw ; => #[law "SQRT(X)"] (law:eval my_firstlaw 4) ;; 2 (law:eval my_firstlaw 9) ;; 3 |
[Top]
Description
The step law symbol is an array alternating laws and numbers. The numbers
divide the real line into disjoint intervals: from minus infinity to num1,
num1 to num2, and numx to positive infinity. A later evaluation uses my_law1
for the first interval, my_law2 for the second, etc.
When evaluating a step symbol at its boundaries, the second law has precedence. If we have the law defined by step( 1, 0, 2*x, 1, -1) and we evaluate it at x=1, the answer is -1 rather than 2.
| ; law "STEP" ; Define an example of a step law (define my_step (law "step( x, 0, x^2, 1, 2-x)")) ;; my_step ; => #[law "STEP(X,0,X^2,1,2-X)"] (define dmy_step (law:derivative my_step)) ;; dmy_step ; => #[law "STEP(1,0,2*X,1,-1)"] (law:eval dmy_step -1) ;; 1 (law:eval dmy_step 2) ;; -1 |
[Top]
Description
surf returns the positions of the defining surface at the parameter value.
In other words, this law symbol is a way to pass a surface into a law
for other purposes, such as evaluation. The dimension of the input, my_surface_law_data,
is two, but when surf is evaluated, it returns an item in three dimensions.
ACIS defines its own parameter range for a surface which is used by this law.
| ; law "SURF" ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; => #[entity 2 1] (define my_surflaw (law "surf(surf1)" (car (entity:faces my_sphere)))) ;; my_surflaw ; => #[law "SURF(SURF1)"] (define my_sveclaw (law "surfvec(law1, vec(x,y,z), vec(a4, a5))" my_surflaw)) ;; my_sveclaw ; my_sveclaw => ; "[SURFVEC(SURF(SURF1),VEC(X,Y,Z), VEC(A4,A5))" ] (law:eval my_sveclaw (list 0 0 1 0 0)) ;; (1 0 0 0) ; The law created takes an xyz vector and a uv ; position on the surface. It returns a uv vector ; in the direction of the given xyz vector at the ; given uv position on the surface. It also returns ; as the last two arguments the uv positions. The uv ; position is echoed. ; Here is an example at the pole. (law:eval my_sveclaw (list 1 1 0 (law:eval "pi/2") 0)) ;; (-1 0 1.5707963267949 0.785398163401155) ; At the pole, this response means that you have to ; turn v by pi/4 to get the correct vector. |
[Top]
Description
When a surface is used as input into a law, it is always followed by an
integer n that specifies its index into the input argument list.
The index numbering starts at 1. For any given index number n,
the argument list has to contain at least n arguments.
| ; law "SURF1" ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; => #[entity 2 1] (define my_surflaw (law "surf(surf1)" (car (entity:faces my_sphere)))) ;; my_surflaw ; my_surflaw ; => #[law "SURF(SURF1)"] (law:eval my_surflaw (list 0 0)) ;; (10 0 0) ; Domain gives first two number as the u range, ; and the next 2 as the v range, which are ; -pi/2 to pi/2 and -pi to pi. (law:domain my_surflaw) ;; "-1.570796 1.570796 -3.1415193 3.1415193\n" ; This is the north pole. (law:eval my_surflaw (list (law:eval "pi/2") 0)) ;; (6.12323399573677e-16 0 10) |
[Top]
Description
Returns the normal to a surface at a given uv position.
ACIS defines its own parameter range for a surface which is used by this law. This law does not normalize the returned vector, because many applications only require the direction of the vector and not its normalized value.
| ; law "SURFNORM" ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; my_sphere => #[entity 2 1] (define my_law (law "surfnorm(surf(surf1))" (car (entity:faces my_sphere)))) ;; my_law ; my_law => #[law "SURFNORM(SURF1)"] (law:eval-vector my_law (list 0 0)) ;; #[gvector -100 0 0] ; We input the uv parameters, (0 0). ; The surface may be flipped in orientation ; from the face, hence the vector in this case ; points into the body. The vector is not normalized. (define my_norm (law "norm(law1)" my_law)) ;; my_norm (law:eval-vector my_norm (list 0 0)) ;; #[gvector -1 0 0] |
[Top]
Description
surfperp returns the uv position on the given surface, my_surface_law_data,
that is closest to the position given by my_position_law. The optional
argument my_uv_guess_law specifies a first guess by the user at the correct
answer, which may speed up the calculation.
| ; law "SURFPERP" ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; => #[entity 2 1] (define my_law (law "surfperp(surf1,vec(x,y,z), vec(a4,a5)))" (car (entity:faces my_sphere)))) ;; my_law ; => #[law "SURFPERP(SURF1,VEC(X,Y,Z),VEC(A4,A5)))"] ; The first guess in this case was uv = (1 1). (law:eval my_law (list 20 0 0 1 1)) ;; (0 0) ; Now define the same law without the optional ; starting evaluation point. (define my_law2 "(law surfperp(surf1,vec(x,y,z)))" (car (entity:faces my_sphere)))) ;; my_law2 ; => #[law "SURFPERP(SURF1,VEC(X,Y,Z))"] (law:eval my_law2 (list 20 0 0)) ;; (0 0) (law:eval my_law2 (list 0 0 30)) ;; (1.5707963267949 -3.14159265358979) ; This answer represents the North pole. |
[Top]
Description
The surfvec returns a parameter vector on my_surflaw at my_paralaw that
is tangent to my_veclaw. It also returns a new parameter value if the
input parameter value is on a singularity.
For example, if my_surflaw is a sphere and the my_paralaw is at the North pole, then this law returns the parameter vector (-1, 0) and the parameter position (pi/2, v), where v indicates the direction my_veclaw is pointing in. Hence, surfvec returns an array of four values: the first two are the parameter vector, and the second two are the potentially new parameter position. The parameter position, except in the case of singularities, equals my_paralaw.
| ; law "SURFVEC" ; Create a surface to evaluate. (define my_sphere (solid:sphere (position 0 0 0) 10)) ;; my_sphere ; => #[entity 2 1] (define my_surflaw (law "surf(surf1)" (car (entity:faces my_sphere)))) ;; my_surflaw ; => #[law "SURF(SURF1)"] (define my_sveclaw (law "surfvec(law1, vec(x,y,z), vec(a4, a5))" my_surflaw)) ;; my_sveclaw ; => ["SURFVEC(SURF(SURF1),VEC(X,Y,Z), VEC(A4,A5))" ] (law:eval my_sveclaw (list 0 0 1 0 0)) ;; (1 0 0 0) ; The law created takes an xyz vector and a uv ; position on the surface. It returns a uv vector ; in the direction of the given xyz vector at the ; given uv position on the surface. It also returns ; as the last two arguments the uv positions. The uv ; position is echoed. ; Here is an example at the pole. (law:eval my_sveclaw (list 1 1 0 (law:eval "pi/2") 0)) ;; (-1 0 1.5707963267949 0.785398163401155) ; At the pole, this response means that you have to ; turn v by pi/4 to get the correct vector. |
[Top]
Description
Most law functions accept numbers as input arguments. This is accomplished
using the identity laws.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
When the identity is used as input into a law, it is sometimes followed by an integer n that specifies its index into the input argument list.
A law expression with a1 and law1 followed by a number and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (the number and then law) and then specify the index number (for example, x and law2, or a1 and law2).
| ; law "T" ; Create a law that needs the first argument. (define my_law (law "t+4")) ;; my_law ; => #[law "T+4"] ; Create an equivalent law. (define my_law2 (law "a1+4")) ;; my_law2 ; => #[law "A1+4"] ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law my_list) ;; 5 ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law2 my_list) ;; 5 |
[Top]
Description
The mathematical definition is:
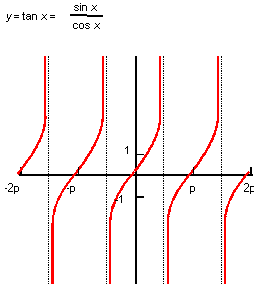
| ; law "TAN(x)" ; Define a law and take its derivative. (define f (law "tan(x)")) ;; f ; => #[law "TAN(X)"] (define df (law:derivative f)) ;; df ; => #[law "SEC(X)^2"] |
[Top]
Description
The mathematical definition is:
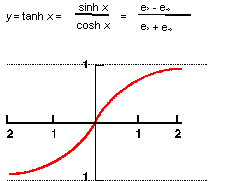
| ; law "TANH(x)" ; Define a law and take its derivative. (define f (law "tanh(x)")) ;; f ; => #[law "TANH(X)"] (define df (law:derivative f)) ;; df ; => #[law "SECH(X)^2"] |
[Top]
Description
The term law symbol returns a single dimensional element (coordinate) of
a multidimensional (my_law1) function. my_term is an integer greater than
zero (0) that specifies which element to grab. This is useful if my_law1
is a curve in x, y, z space, and one of the coordinates
needs to be isolated.
In other words, assume my_law is a vector field defined by vec(x, x+1, x+2, x+3). A declaration like (law:eval term(my_law, 4) 1) evaluates the fourth coordinate of my_law, x+3, at the value 1. It returns 4. A declaration like (law:eval term(my_law, 3) 1) evaluates the third coordinate of my_law, x+2, at the value 1. It returns 3.
The next example first creates an edge, called my_edge. Then it creates a law, called my_law, that is the composition of three laws. The map law symbol maps that parameter domain of my_edge or edge1 to the closed interval [0,1]. The term law symbol returns the x coordinate of the cur function that returns the position of the curve edge1. Next my_maxpoint is defined as the numerical minimum of the law my_law over the domain [0.5,1]. Then my_testcur is evaluated at my_maxpoint, and the result is plotted. The plotted point represents the point on the curve that has the lowest x coordinate.
| ; law "TERM" ; Create a vector field. (define my_law (law "vec(x, y, z, x+8)")) ;; my_law ; => #[law "VEC (X,Y,Z,X+8)"] ; Pick off the third coordinate of the vector, ; which is the z term of vec. (define my_third (law "term ( law1, 3)" my_law)) ;; my_third ; => #[law "TERM(VEC (X,Y,Z,X+8),3)"] ; Pick off the fourth coordinate of the vector, ; which is the x+3 term of vec. (define my_fourth (law "term ( law1, 4)" my_law)) ;; my_fourth ; => #[law "TERM (VEC (X,Y,Z,X+8),4)"] ; Create evaluation numbers. Because vec has ; x, y, and z (x0, x1, and x2), the input list ; has to have three items. (define my_input (list 2 4 6)) ;; my_input ; => (2 4 6) ; Evaluate the third coordinate with the input. (law:eval my_third my_input) ;; 6 ; z gets assigned 6. (law:eval my_fourth my_input) ;; 10 => ; x gets assigned 2. x+8 is 10. ; Another example. ; Create the points for a test curve. (define my_plist (list (position 0 0 0) (position 20 20 20) (position -20 20 20) (position 0 0 0))) ;; my_plist (define my_start (gvector 1 1 1)) ;; my_start ; => #[gvector 1 1 1] (define my_end (gvector 1 1 1)) ;; my_end ; => #[gvector 1 1 1] (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; => #[entity 2 1] ; Create a curve law. Get just the x component of ; the curve and map it between [0,1]. (define my_curlaw (law "map (term (cur (edge1),1),edge1)" my_testcur)) ;; my_curlaw ;; => #[law "MAP (TERM (CUR (EDGE1),1),EDGE2)"] ; Find its minimum. (define my_min (law:nmin my_curlaw 0 1)) ;; my_min ; => 0.713060255033984 ; Plot and mark that point. (define my_minpoint (dl-item:point (curve:eval-pos my_testcur my_min))) ;; my_minpoint ; => #[dl-item 4025e708] (dl-item:display my_minpoint) ;; () |
[Top]
Description
Parsing actually involves the * character. my_law1 and my_law2 can be any
valid law. Both my_law1 and my_law2 can be multiple dimensions; the smaller
of the two is padded with zeros.
The times law supports implied multiplication. This means that a constant (integer or real) placed in front of a variable and not already part of the previous variable is implied to be multiplication. The parser takes the longest recognizable string possible before determining implied multiplication. For example, 2XY implies 2*X*Y, while X2Y implies X2*Y. This facilitates entering equations in a more natural fashion, such as 2X^2+3.87Y+12Z^3 implies 2*(X^2)+(3.87)*(Y)+12*(Z^3).
| ; law "*" ; Create a simple law. (define my_firstlaw (law "x^2")) ;; my_firstlaw ; => #[law "X^2"] ; Create a second simple law. (define my_secondlaw (law "x*3")) ;; my_secondlaw ; => #[law "X*3"] ; Create a third law that takes ; two laws as input arguments. (define my_complexlaw (law "law2-3*law1" my_firstlaw my_secondlaw)) ;; my_complexlaw ; => #[law "X*3*3*X^2"] (law:eval my_complexlaw 2) ;; -6 ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate implied multiplication (law:eval "yz" my_list) ;; 6 ; Law parsing takes longest string possible ; before doing implied multiplication. (law:eval "u4z" my_list) ;; 12 ; Evaluate implied multiplication (define my_law (law "a1b2c3d4e5f6Z7")) ;; my_lawv ; my_law => #[law "A1*B2*C3*D4*E5*F6*Z7"] (law:eval my_law my_list) ;; 5040 |
[Top]
Description
The trans law symbol requires that my_law return positions. It produces
positions that have been transformed by the my_transf. rotate is used
on vectors, while trans is used to transform positions.
| ; law "TRANS(trans1)" ; Create a transform, and then create its inverse. (define my_trans_rot (transform:rotation (position 0 0 0) (gvector 1 0 0) 90)) ;; my_trans_rot ; => #[transform 1075284160] (define my_trans_move (transform:translation (gvector 1 0 0))) ;; my_trans_move ; => #[transform 1075284848] (define my_t_comp (transform:compose my_trans_rot my_trans_move)) ;; my_t_comp (define my_law (law "trans(vec(x,y,z),trans1") my_t_comp)) ;; my_law ; => #[law "TRANS(VEC(X,Y,Z),TRANS1)"] ; This transforms the given law "VEC(X,Y,Z)" by ; the supplied transform, my_t_comp (law:eval my_law (list 0 0 1)) ;; (1 -1 6.12323399573677e-17) ; In this example, the input vector is (0, 0, 1). ; It gets rotated by 90 degrees, causing y to be ; -1 and then gets moved along x axis by 1. ; z is approximately zero. |
[Top]
Description
Some law functions, such as rotate and trans, accept transforms as input
arguments.
When a transform is used as input into a law, it is always followed by an integer n that specifies its index into the input argument list. The index numbering starts at 1. For any given index number n, the argument list has to contain at least n arguments.
A law expression with trans1 and law1 followed by a transform and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for example, law and then transform) and then specify the index number (trans2 and law1).
If the law to which a trans# is passed returns a vector, the law to use is rotate. If the law to which a trans# is passed returns a position, the law to use is trans.
| ; law "TRANS1" ; Create a transform, and then create its inverse. (define my_trans_rot (transform:rotation (position 0 0 0) (gvector 1 0 0) 90)) ;; my_trans_rot ; => #[transform 1075259928] (define my_trans_move (transform:translation (gvector 1 0 0))) ;; my_trans_move ; => #[transform 1075260672] (define my_t_comp (transform:compose my_trans_rot my_trans_move)) ;; my_t_comp ; => #[transform 1075261368] (define my_law (law "trans(vec(x,y,z),trans1") my_t_comp)) ;; my_law ; my_law => #[law "TRANS(VEC(X,Y,Z),TRANS1)"] ; This transforms the given law "VEC(X,Y,Z)" by ; the supplied transform, my_t_comp (law:eval my_law (list 0 0 1)) ;; (1 -1 6.12323399573677e-17) ; In this example, the input vector is (0, 0, 1). ; It gets rotated by 90 degrees, causing y to be ; -1 and then gets moved along x axis by 1. ; z is approximately zero. |
[Top]
Description
This test is used initially as part of selective booleans and sweeping.
This can be used to specify which parts of a sweep operation are to be
kept. This is a shorthand way of stating that all cells are to be kept.
This law symbol has other uses not yet exploited yet.
| ; law "TRUE(x)" ; Create a sweep example to show selective booleans. (define blank (solid:block (position -10 -10 5) (position 10 10 30))) ;; blank ; blank => [entity 2 1] (define b2 (solid:block (position -5 -10 10) (position 10 10 15))) ;; b2 (define b3 (solid:block (position -5 -10 20) (position 10 10 25))) ;; b3 (solid:subtract blank b2) ;; [entity 2 1] (solid:subtract blank b3) ;; [entity 2 1] (define profile (edge:ellipse (position 0 0 0) (gvector 0 0 1)2)) ;; profile (define path (edge:linear (position 0 0 0) (position 0 0 35))) ;; path (define opts (sweep:options "to_body" blank "bool_type" "unite" "keep_law" "TRUE")) ;; opts (sweep:law profile path opts) ;; |
[Top]
Description
The twist law takes in one value and returns a vector that is formed by
rotating my_vector_field about my_path_law by an angle (in radians) given
by my_twist_law. my_vector_field is a law that takes in one value and
returns a vector. my_path_law is a law that takes in one value and returns
a position. my_twist_law is a law that takes one value and returns one
value. This is used for creating rail laws for sweeping with twist.
| ; law "TWIST" ; Create a law. ; This law produces a vector field that sweeps out a ; helix about the x-axis. ; The x-axis is the path. The starting vector field ; is a constant vector pointing in the z-direction. ; The twist vector is linear, y=x. (define my_law (law "twist(vec(0,0,1), vec(x,0,0),x)")) ;; my_law ; => #[law "TWIST(VEC(0,0,1),VEC(X,0,0),X)"] (law:eval-vector my_law 0) ;; #[gvector 0 0 1] (law:eval-vector my_law 1) ;; #[gvector 0 -0.841470984807897 0.54030230586814] (law:eval-vector my_law (law:eval "pi")) ;; #[gvector 0 -1.22464679914735e-16 -1] ; This is essentially pointing straight down. |
[Top]
Description
Most law functions accept numbers as input arguments. This is accomplished
using the identity laws.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
When the identity is used as input into a law, it is sometimes followed by an integer n that specifies its index into the input argument list.
A law expression with a1 and law1 followed by a number and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for example, number and then law) and then specify the index number (x and law2, or a1 and law2).
| ;law "U" ; Create a law that needs the first argument. (define my_law (law "u+4")) ;; my_law ; => #[law "U+4"] ; Create an equivalent law. ;; my_law2 ; => #[law "A1+4"] ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law my_list) ;; 5 ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law2 my_list) ;; 5 |
[Top]
Description
The variables to this law function are laws. However, my_pos, my_axis,
and my_direction have to return three elements [i.e., VEC(0, 0, 0)], while
my_distance has to return one element.
| ; law "UNBEND" ; Create the geometry to illustrate law. (define s1 (solid:cylinder (position 0 0 0) (position 0 0 10) 10) ) ;; s1 (define s2 (solid:cylinder (position 0 0 0) (position 0 0 10) 5) ) ;; s2 (define subtract (bool:subtract s1 s2)) ;; subtract (define block (solid:block (position 0 -10 -10) (position 10 10 10))) ;; block (define subtract2 (bool:subtract subtract block)) ;; subtract2 ; OUTPUT Original ; Define the law to unbend the half cylinder. (define law1 (law "unbend ( vec (0,0,0), vec (0,0,1), vec (-1,0,0), 5)")) ;; law1 ; Apply the unbend law. (define unbend (law:warp subtract2 law1)) ;; unbend ; OUTPUT Result
Figure 1. unbend |
[Top]
Description
Most law functions accept numbers as input arguments.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
| ;law "V" ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate the laws. ; Use just the first input list item. (law:eval "a1+4" my_list) ;; 5 ; Use just the second input list item. (law:eval "v" my_list) ;; 2 ; Use just the second input list item. (law:eval "a2+4" my_list) ;; 6 ; Use just the third input list item. (law:eval "a3+4" my_list) ;; 7 ; Use just the fourth input list item. (law:eval "a4+4" my_list) ;; 8 |
[Top]
Description
This law is a way of combining several sublaws, each of one dimension,
into a single law that has several dimensions. All sublaws have to return
one dimensional items, although they can have multiple input items.
| ; law "VEC" ; Create two gvectors. (define g1 (law (gvector 1 1 0))) ;; g1 ; => #[law "VEC(1,1,0)"] (define g2 (law (gvector 0 0 1))) ;; g2 ; => #[law "VEC(0,0,1)"] (define my_law (law "law1+law2" g1 g2)) ;; my_law ; => #[law "VEC(1,1,0)+VEC(0,0,1)"] ;; #[gvector 1 1 1] ; Another example. ; Create a vec law. (define my_vec (law "vec( x^2, 2*x^3, x+1)")) ;; my_vec ; => #[law "VEC(X^2,2*X^3,X+1)"] ; Evaluate the law at a value of x. (law:eval-position my_vec 2) ;; #[position 4 16 3] (define dmy_vec (law:derivative my_vec)) ;; dmy_vec ; => #[law "VEC(2*X,6*X^2,1)"] ; Create another vector with two input arguments. (define my_vec2 (law "vec( x+y, y^2, X^2)")) ;; my_vec2 ; => #[law "VEC(X+Y,Y^2,X^2)"] ; Evaluate the law at a value of x and y. (law:eval my_vec2 (list 2 1)) ;; (3 1 4) |
[Top]
Description
A wire is parameterized from 0 to the length of the wire. This symbol returns
the position of the wires component edges. The parameterization has been
linearly scaled to match the total length of the edge.
ACIS parameterization is not the arc length. The wire law returns the position as a function of arc length, in as much linear scaling as the subedges can accomplish. In the case of lines and arcs, the parameterization is exactly the arc length. Curves which are not parameterized with constant speed may have some variance internal to them. All curves other than arcs and lines have non-constant speed.
| ; law "WIRE" ; Create an edge. (define my_edge (edge:circular (position 0 0 0) 20)) ; my_edge ; => #[entity 2 1] ; Create a wire body. (define my_wire (wire-body my_edge)) ;; my_wire ; => #[entity 3 1] ; Input this wire into a law. (define my_law (law "wire(wire1)" my_wire)) ;; my_law ; => #[law "WIRE(WIRE1)"] ; Evaluate this law at a ; parameter value. (law:eval-position my_law 2) ;; #[position 19.9000833055605 1.99666833293656 0] |
[Top]
Description
Some law functions, such as wire and dwire, accept wires as input arguments.
When a wire is used as input into a law, it is always followed by an integer n that specifies its index into the input argument list. The index numbering starts at 1. For any given index number n, the argument list has to contain at least n arguments.
A law expression with wire1 and law1 followed by a wire and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for exmaple, law and then wire) and then specify the index number (wire2 and law1).
A wire law is parameterized by the arc length to be equal to the arc length at the end points. Thus, parameterization works to the ends of edges but not to the middle of an edge unless the edge has a constant speed, such as straight lines and circles. The parameter spacing on edges with non-constant speeds is not even.
| ; law "WIRE#" ; Create the points for a test curve. (define my_plist (list (position 0 0 0) (position 20 20 20) (position -20 20 20) (position 0 0 0))) ;; my_plist (define my_start (gvector 1 1 1)) ;; my_start ; => #[gvector 1 1 1] (define my_end (gvector 1 1 1)) ;; my_end ; => #[gvector 1 1 1] (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; => #[entity 2 1] (define my_wirebody (wire-body my_testcur)) ;; my_wirebody ; => #[entity 3 1] ; Creation of wirebody removed my_testcur. ; Recreate for use later. (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; => #[entity 4 1] ; Create a wire law. (define my_wirelaw (law "map(term (wire (wire1),1),wire2") my_wirebody)) ;; my_wirelaw ; => #[law "MAP(TERM (WIRE (WIRE1),1),WIRE2)"] ; Find its minimum. (define my_min (law:nmin my_wirelaw 0 1)) ;; my_min ; => 0.713060255033983 ; Plot and mark that point. (define my_minpoint (dl-item:point (curve:eval-pos my_testcur my_min))) ;; my_minpoint => #[dl-item 22F733F8] (dl-item:display my_minpoint) ;; () |
[Top]
Description
Most law functions accept numbers as input arguments. This is accomplished
using the identity laws.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
A law expression with a1 and law1 followed by a number and a law is invalid, because each is requesting a different argument type as the first element of the argument list. To correct this problem, specify the ordering of the arguments in the input argument list (for example, number and then law) and then specify the index number (x and law2, or a1 and law2).
| ;law "X" ; Create a law that needs the first argument. (define my_law (law "x+4")) ;; my_law ; => #[law "X+4"] ; Create an equivalent law. (define my_law2 (law "a1+4")) ;; my_law2 ; => #[law "A1+4"] ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law my_list) ;; 5 ; Evaluate this law. The first argument in ; the input list is used, all others are ignored (law:eval my_law2 my_list) ;; 5 |
[Top]
Description
Most law functions accept numbers as input arguments.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
| ;law "Y" ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate the laws. ; Use just the first input list item. (law:eval "a1+4" my_list) ;; 5 ; Use just the second input list item. (law:eval "y" my_list) ;; 2 ; Use just the second input list item. (law:eval "a2+4" my_list) ;; 6 ; Use just the third input list item. (law:eval "a3+4" my_list) ;; 7 ; Use just the fourth input list item. (law:eval "a4+4" my_list) ;; 8 |
[Top]
Description
Most law functions accept numbers as input arguments.
Any letter of the alphabet followed by an integer n can be used.
There are six individual letters (E, O, T, U, V, X, Y, and Z) that can
be used with or without integer subscripts, but can have different meanings
in a law depending on whether or not a subscript is used.
T=U=X=A1=B1=...=T1=U1=V1=W1=X1=Y1=Z1
V=Y=A2=B2=...=T2=U2=V2=W2=X2=Y2=Z2
Z=A3=B3=...=T3=U3=V3=W3=X3=Y3=Z3
An=Bn=...=Zn.
| ;law "Z" ; Create an input list to pass to the law. (define my_list (list 1 2 3 4 5 6 7)) ;; my_list ; Evaluate the laws. ; Use just the first input list item. (law:eval "a1+4" my_list) ;; 5 ; Use just the second input list item. (law:eval "a2+4" my_list) ;; 6 ; Use just the third input list item. (law:eval "z" my_list) ;; 3 ; Use just the third input list item. (law:eval "a3+4" my_list) ;; 7 ; Use just the fourth input list item. (law:eval "a4+4" my_list) ;; 8 |
[Top]
© 1989-2006 Spatial Corp., a Dassault Systèmes company. All rights reserved.