Edges
An edge is the topology associated with a curve. The direction of an edge can be either the same direction as its underlying curve, or it can be the opposite direction. If it is the same as the curve direction, the edge's sense relative to the underlying curve is forward; otherwise, its sense is reversed. Each edge contains a record of its sense relative to its underlying curve.
An edge is bounded by one or more vertices, referring to one vertex at each end. If the reference at either or both ends is NULL, the edge is unbounded in that direction. If the underlying curve is infinite, so is the unbounded edge. When the curve is closed, the vertex references must both be the same or both NULL. If both vertex references are NULL, the edge is the whole curve; unless the curve is open and bounded, in which case the vertices must coincide with the curve ends.
A special case occurs when the geometry pointer is NULL and both vertex pointers point to the same vertex; for example, at the apex of a cone. Few ACIS operations work correctly with edges that have one or both end vertex pointers NULL.
An important feature of ACIS edge representation is the arrangement of the coedges around an edge. (Refer to section Coedges for more information.) If only two faces meet at an edge, the two coedges from those faces point to each other through the coedge partner pointers. (If there is only one coedge, its partner pointer is NULL.) If more than two faces meet at an edge, the coedges are in a circular linked list. The order of the list is important, because it represents the radial ordering of the faces about the edge in a counterclockwise direction. The following figure shows a sheet body that contains a non-manifold (more than two faces incident) edge. The edge is directed such that it is coming toward the reader, and the coedges are ordered counterclockwise about it in the partner list as indicated by the arrow.
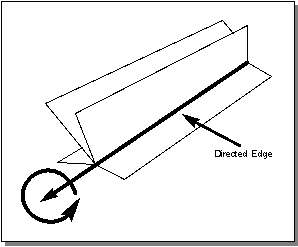
Figure. Radial Coedge Ordering
The purpose of radial coedge ordering becomes clear during traversal of an ACIS model that contains faces embedded with a solid region, such as in a 3D finite element model. Moving from a face across an edge to the radially closest adjacent face is a simple list operation, rather than a geometric operation as when coedges are not ordered. For example, moving to the face that is closest to the front (outward normal) side of a face is done by moving to the next partner pointer, if the original face coedge is FORWARD. If the original face coedge is REVERSED, moving to the closet face is done by moving to the previous partner pointer (obtained by walking all the way around the list).
In a non-manifold body shell, the edge may be adjacent to more than two faces. A non-manifold body is shown in the following figure. An edge common to four faces is at each point where the cylinder is tangent to the outside edge of the block. In the example, edge ab is common to two faces on the inside wall of the cylinder (abcd and abfe) and two faces on the outside of the block (abgh and abjk). Edge ab is common to all four faces. When there are more than two coedges associated with an edge, they are ordered counterclockwise about the edge.
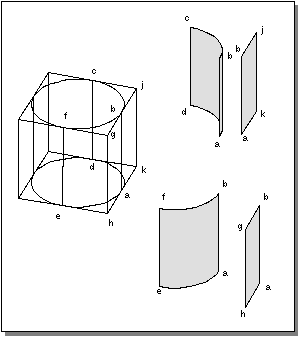
Figure. Non-manifold Body with Common Edge
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.