Coedges
A coedge records the occurrence of an edge in a loop of a face. The introduction of coedges permits edges to occur in one, two or more faces, and so makes possible the modeling of sheets and solids (manifold or not). A loop refers to one coedge in the loop, from which pointers lead to the other coedges of the loop. Coedges in a loop are ordered in a continuous path around the loop and are doubly-linked. If a loop is not a circular list, the loop points to the first coedge.
In a manifold solid body shell, each edge is adjacent to exactly two faces; therefore, the edge has two coedges, each associated with a loop in one of the faces (the two faces can be the same, and even the loops can be the same). In this case, the two coedges always go in opposite directions along the edge. In a non-manifold body shell, there may be more than two coedges associated with an edge. In this case, they are ordered counterclockwise about the edge. Refer to section Edges for more information.
In the following figure, an isometric view of a solid shows three faces. Each face is bounded by a loop of coedges. Each edge (corner of the block) has two coedges, one for each face that is adjacent to the edge. Each coedge is coincidental with the edge adjacent and parallel to it.
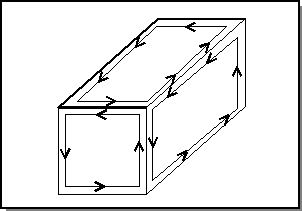
Figure. Loops of Coedges on Faces
Coedges in a loop are oriented so that looking along the coedge with the outward pointing face normal upwards, the face is on the left. In the following figure, the directions of the face normals (blue arrows) and coedges (red arrows) for several faces of a body are shown to illustrate this orientation.
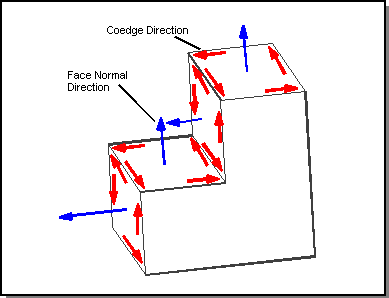
Figure. Coedge Orientation with Face Normals
In a sheet body, there may be edges that have only one coedge. These are knows as free edges, and they mark the boundary of a sheet. If the face attached to the coedge is single-sided, the inside and outside of the associated shell are not well-defined near the edge, and so the shell is necessarily incomplete. (Refer to section Shells for more information.)
Even though the edges of a wire meet no faces, each is given an associated coedge whose pointers link the edge to its neighbors.
The direction of a coedge can be either the same direction as its edge, or it can be the reverse of the edge direction. If it is the same as the edge direction, the coedge's sense relative to the edge direction is forward; otherwise, its sense is reversed. Each coedge contains a record of its sense relative to its edge.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.