Sequences of Blended Edges
A blend sequence is a series of connected edges that are to be blended in a single operation. The vertices where two blended edges meet are categorized as follows:
- Smooth
- Two blended edges meet tangentially at a vertex, and any number of non-blended edges may meet as long as they are smooth edges. A vertex with this configuration is called a biblend.
- Non-smooth
- Blended edges do not meet tangentially, or there are non-smooth, non-blended edges at the vertex. This results in a mitered blend.
- Closed/Open
- Either type of sequence may be open or closed. A closed sequence consists of a closed loop of blended edges. In a closed sequence, there is no need to find end capping faces for the blend surfaces (side caps can still occur).
Bi-Blend
A bi-blend is an internal vertex at which two edges meet tangentially and have compatible blend attributes. Any number of smooth, non-blended edges may meet at the vertex. At a bi-blend vertex, the blend surfaces from the two blended edges mate exactly to form a smooth continuous blend across the vertex.
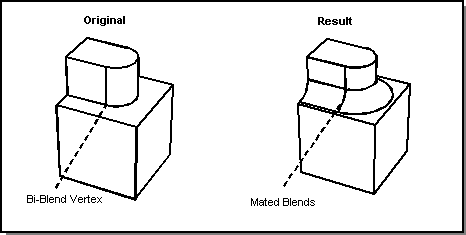
Figure. Smooth Sequence Bi-Blend
Mitered Blends
A mitered blend is the case in which the vertex is an internal vertex at which two edges do not meet each other tangentially or there are non-smooth, non-blended edges present at the vertex.
A miter surface is used to calculate the cross curves when blending two edges that do not meet tangentially. In the special case of constant rounded blends on coplanar straight or circular edges, a curved miter surface is constructed instead of a plane.
The two blended edges need not have the same blend attributes, but they must have the same convexity. At most, two other edges may be incident at the vertex, and they must be non-smooth. If two other edges are present, they must be separated by the two edges being blended. The following figure shows a concave mitered blend.
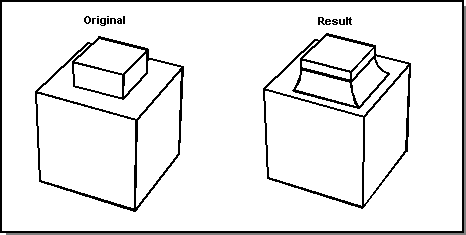
Figure. Concave Mitered Blend
Complex Miter
If two blend sheets do not meet smoothly and do not match at their ends, this condition requires special processing. One of the side surfaces must be extended as a partial end cap. This may happen if the two blends have different radii. The following figure shows a concave, complex miter.
Complex miters might also be required if a common side surface is not perpendicular to the intervening edge. This condition also requires that one of the side surfaces be extended as a partial end cap. Figure. Complex Mitered Blend shows such a mitered blend. The blends have the same radii, but the miter is complex, because the two upper spring curves intersect the vertical edge at different points.
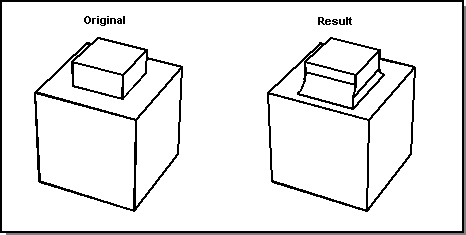
Figure. Concave Complex Miter
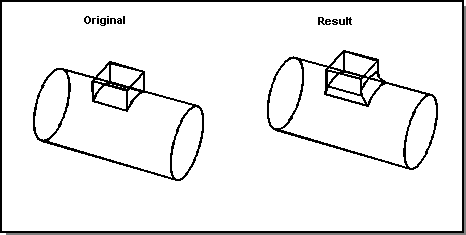
Figure. Complex Mitered Blend
Closed Sequences
A closed sequence of blended edges and bi-blend vertices has no open ends and no end caps. Internal vertices in the sequence may be smooth (a bi-blend) or non-smooth (a mitered joint). The following figure shows a closed sequence with both bi-blends and miters. The term periodic sequence is sometimes used to refer to a closed sequence with no miters or vertex blends.
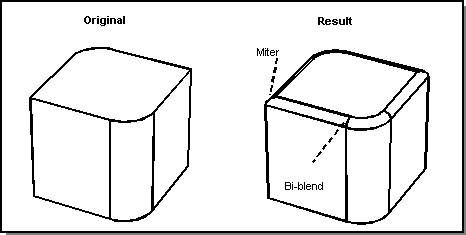
Figure. Closed Sequence
Open Ends and End Caps
At the end of a blend sequence (an open end of the sequence), the blend sheet must be fitted exactly to the original model. When possible, a face (or faces) in the model will be intersected with the blend sheet to trim the sheet exactly to the model. When no model faces intersect the blend sheet, ACIS will attempt to extend existing model faces to close off the end of the blend. The following figure shows an example of such an end cap.
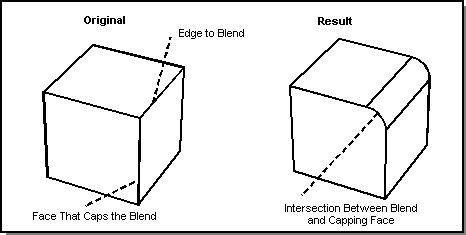
Figure. Identifying End Caps
Multiple Capping Faces
The blend sheet may intersect multiple capping faces in the body. The following figure shows a blend sheet that is intersected with two of the faces in order to trim the sheet to the correct size.
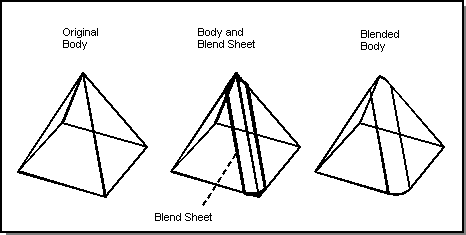
Figure. Multiple Capping Faces
Extending Capping Faces
If a blend has an open end at a mixed convexity vertex, a face in the body may need to be extended to create the blends end cap. A mixed convexity vertex is a vertex at which the blended edge meets other edges whose convexity is not the same as the blended edges. If the capping faces are spline surfaces, then an extension of the capping face is created so that the blend surface is guaranteed to intersect with the capping surface.
In the following figure, two faces, A and B, are extended in order to close off the end of the blend.
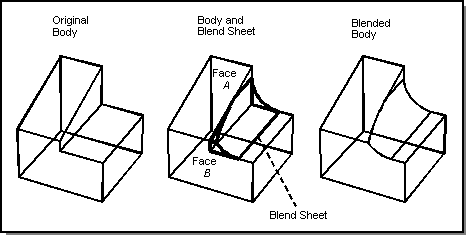
Figure. Extended Capping Faces
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.