Accessing Laws through String Parsing
Although accessing the law class methods directly is possible, it is much more likely that the APIs and law string parsing will be employed. This technique is easier and more straightforward to implement.
A law mathematical function is a character string enclosed in quotation marks. The law symbols used in the mathematical function are very similar to common mathematical notation and to the adaptation of mathematical notation for use in computers. The valid syntax for the character strings are given in the law symbol templates. The law mathematical functions support nesting of law symbols.
Once the character string for the law mathematical function has been created, it is passed to the api_str_to_law API along with a pointer to an output law, an array of law data, and the size of the law data array. The API parses the character string, creates the required output law class instances, and returns the address for the top-level output law class instance.
Note: The api_str_to_law function does not do any type checking to make sure that the law string tags agree with their law_data arguments.
The disadvantage of using character strings with law symbols is that it takes more processing time to parse the strings. The advantage of using them is that they are simpler than using the law class constructors directly. The creation of supporting law class instances is managed behind the scenes.
In the following example, my_law is an instance of the law class which holds the mathematical function x2y2. The law symbol syntax for my_law is (x^2) * (y^2). Extra spaces are ignored, such as those setting off the * character for times. All derived laws obey standard precedence for mathematical evaluation. Because exponents have precedence over multiplication, my_law could have been written without the parenthesis as x^2*y^2.
Example 1 is a C++ code fragment that calculates the first and second partial derivatives with respect to x and y of the mathematical function x2y2, and then evaluates these for differing values of x and y. The partial derivatives are shown in the figure below.
C++ Example
| // Create special law:
// my_law is x squared times y squared ; (x^2) * (y^2) char my_function_string[50]; strcpy(my_function_string, "(x^2)*(y^2)"); double my_input[2]; // Convert a character string into law mathematical // function class law *my_law; api_str_to_law( my_function_string, &my_law, 0, NULL); // Create partial derivatives // 1st partial derivative wrt x = (2*(y^2)*x) // my_law->evaluateD( my_input, 1); // acquired in another way // 1st partial derivative wrt y = (2*(x^2)*y) law *dy = my_law->derivative(1); // 2nd partial derivative wrt x = (2*(y^2)) // my_law->evaluateD( my_input, 2); // acquired in another way // 2nd partial derivative wrt y = (2*(x^2)) law *ddy = dy->derivative(1); // partial wrt x, partial wrt y = 4*x*y law *dxdy = dy->derivative(0); // Use new law instance to evaluate function for (int x=0; x<10; x++) { for (int y=0; y<10; y++) { printf("input are: %d %d /t", x, y); my_input[0] = x; my_input[1] = y; // Evaluate original function // my_law = (x^2) * (y^2) // This is built into the original function. my_answer = my_law->evaluateS(my_input); printf("output is: %lf /t", my_answer); // Evaluate 1st partial derivative wrt x = (2*(y^2)*x) // This is built into the original function. my_answer = my_law->evaluateD(my_input, 1); printf("1st derivative wrt x is: %lf /t", my_answer); // Evaluate 1st partial derivative wrt y = (2*(x^2)*y) my_answer = dy->evaluateS(my_input); printf("1st partial wrt y is: %lf /t", my_answer); // Evaluate 2nd partial derivative wrt x = (2*(y^2)) // This is built into the original function. my_answer = my_law->evaluateD(my_input, 2); printf("2nd partial wrt x is: %lf /t", my_answer); // Evaluate 2nd partial derivative wrt y = (2*(x^2)) my_answer = ddy->evaluateS(my_input); printf("2nd partial wrt y is: %lf /t", my_answer); // Evaluate partial wrt x, partial wrt y = 4*x*y // This is built into the derived function. my_answer = dxdy->evaluateS(my_input); printf("partial wrt x, partial wrt y = %lf /n", my_answer); } } // Clean up memory usage my_law->remove(); dy->remove(); ddy->remove(); dxdy->remove(); |
Example. API and Law Classes for Derivatives
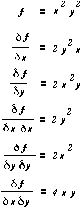
Figure. Partial Derivatives of x2y2
The low level implementation of laws in Scheme uses APIs and law string parsing. Laws can be used independently of ACIS to perform mathematical calculations. They can also be used within ACIS to find geometric information not otherwise so easy to obtain, such as minimum and maximum. Laws can be used to help define geometry in wire offsetting and sweeping. In Scheme, these are the wire-body:offset and sweep:law extensions.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.