Analyzing Models
Creation and modification can be considered the major tasks associated with solid modeling. However, analysis is also important because it can help define geometry and can verify model geometry.
An earlier section discussed how transformations are used to orient and position entities, such as solid primitives, after creation. Suppose that a unique surface A was created using some surface creation technique, such as net surfaces or skinning, and that a newly created entity B is now to be positioned and oriented with respect to some geometric property of A. While transformations may provide a means of moving and orienting entity B, analysis helps determine where to move entity B and how to orient it.
ACIS has these main areas of analysis:
- Physical Properties
- Provides surface area, volume, and center of gravity information about a model.
- Object Relationships
- Provides information regarding proximity on a plane, on a line, parallelism, perpendicularity, for example.
- Geometric Analysis
- Uses ACIS laws to find out specific mathematical answers about geometric elements, such as the nth derivative of a curve at a given point, and numerical maxima and minima.
- Cellular Topology
- Does not perform any analysis in its own right, but is a data structure for storing information about the model that custom applications can employ for their own analysis operations.
All geometric entities provide methods for querying properties. However, the data structures do not explicitly store information such as the point of the curve where the radius of curvature is minimized, the tangent vector from a given point on an edge, the normal vector from a given point on a surface, or the numerical nth derivatives of points along a curve to determine continuity. There are many geometric properties that you might want to know when analyzing your model.
ACIS laws provide powerful analysis features. Not only can independent calculations be carried out on complex mathematical functions, but calculations can also be carried out using geometric entities as input. ACIS laws expand significantly the type of analysis that can be performed in creating and manipulating models. The complexity of the analysis is determined by the complexity of the defining laws and geometric elements.
In the following example, illustrates determination of the maximum radius of curvature of a point on a spline edge. After the spline edge is created, it is passed into a curvature law function and parameterized from 0 to 1. Then, the numerical maximum of curvature is determined for that edge. This is illustrated in the following figure.
Scheme Example
| ; Define a list of points for a spline edge. (define my_plist (list (position 0 0 0)(position 20 20 0) (position 40 0 0)(position 60 25 0) (position 40 50 0)(position 20 30 0) (position 0 50 0))) ;; my_plist (define my_start (gvector 1 1 0)) ;; my_start (define my_end (gvector -1 1 0)) ;; my_end (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur (define my_law (law "map(Curc(edge1),edge1)" my_testcur)) ;; my_law (define my_maxpoint (law:nmax my_law 0 1)) ;; my_maxpoint ; All curves in Scheme are parameterized from 0 to 1. (define my_maxposition (curve:eval-pos my_testcur my_maxpoint)) ;; my_maxposition ; my_maxposition => ; #[position 19.9659145308554 29.9949779948174 0] (define my_point (dl-item:point my_maxposition)) ;; my_point ; Create a display list item so the point can be ; viewed. This point will not be saved to a SAT file. (dl-item:display my_point) ;; () ; To no longer display this point, use: ; (dl-item:erase my_point) |
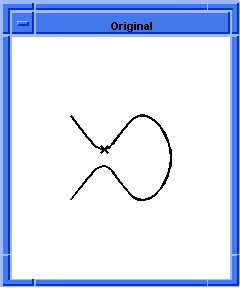
Figure. First Maximum Point on a Test Curve
The following example demonstrates how analysis is used to determine physical properties of a model. This example also illustrates transforms and Booleans.
The example creates and copies a cylinder. The first instance of the cylinder has a transform applied to it which rotates it 90 degrees. Then, the two cylinders are intersected leaving only the portion of each cylinder that is common to both. This new solid model can be queried for its physical properties, such as its surface area, volume, and center of gravity.
Scheme Example
| ; Purpose: to show that the volume of the intersection of ; two cylinders of unit radius, whose axes intersect at ; an angle of 90 degrees is 5 1/3. (define mpo (massprops:options)) ;; mpo (massprops-options:set-level mpo "volume-only") ;; "volume-centroid-and-inertia" (massprops-options:set-req-rel-accy mpo 0.0000001) ;; 0.01 (define mp (body:massprops my_intersect mpo)) ;; mp (massprops:get-volume mp) ;; 5.33333266797548 (massprops:get-rel-accy-vol-achieved mp) ;; 2.15514210961525e-007 |
Some of the Scheme extensions related to analysis are:
- gvector:length
-
Gets the length of a gvector.
- gvector:parallel?
- Determines if two gvectors are parallel.
- gvector:perpendicular?
- Determines if two gvectors are perpendicular.
- law:derivative
- Creates a law object that is the derivative of the given law with respect to the given variable.
- law:eval
- Evaluates a given law or law expression with the specified input and returns a real or list of reals.
- law:eval-position
- Evaluates a given law or law expression with the specified input and returns a position or a par-pos.
- law:eval-vector
- Evaluates a given law or law expression with the specified input and returns a gvector.
- law:nderivative
- Computes the numerical derivative of a law function with respect to a given variable, a given number of times.
- law:nintegrate
- Computes the numerical integral of the given law function over the specified range.
- law:nmax
- Computes where a law is the maximum over a given interval.
- law:nmin
- Computes where a law is the minimum over a given interval.
- law:nroot
- Computes all of the roots of a law function over a given interval.
- law:nsolve
- Computes all the locations where two laws are equal to one another over a given interval.
- law:simplify
- Creates a law which is the algebraic simplification of the given law.
- par-pos:distance
- Gets the 2D distance between two par-pos.
- position:closest
- Gets the position from a list of positions that is closest to a given position.
- position:distance
- Gets the distance between two positions.
- position:project-to-line
- Gets the projection of a position on to a line.
- position:project-to-plane
- Gets the projection of a position onto a plane.
- solid:classify-position
- Classifies a point with respect to a solid.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.