Constructors
The Constructors Component (CSTR), is one of most important and frequently used components in ACIS. It contains API functions to create, edit, and analyze geometry. Geometry creation includes lines, curves, arcs, planes, wires, prisms, cuboids, pyramids, spheres, splines, tori, etc. As part of its analysis capabilities, it locates faces, edges, and vertices, and performs wire length, face area, and body physical property calculations.
Topics include:
Adaptive Subdivision Algorithm for Mass Properties Calculations
In the ACIS R11 release, a new Adaptive Subdivision algorithm was introduced for mass properties calculations, coupled with stricter convergence criteria - both numerical and geometric.
The primary aim of these changes was to achieve more accurate and reliable answers in known difficult cases by tightening the convergence criteria. The introduction of an adaptive subdivision technique was necessary in order to maintain (and in some cases dramatically improve) performance by avoiding extra work in areas where the numerical integration converges quickly.
With any iterative numerical integration algorithm, the determination of convergence is of critical importance to the accuracy and performance of the algorithm. At each stage, an approximation to the integral is generated, which must be judged as to its accuracy - typically, by requiring the result to be within a given tolerance of the true solution. In general, for a non-analytic integrand, it is not possible to construct true error bounds on the solution, as these typically depend on finding a maximum value of a derivative of the integrand.
When only numerical results are available, the only way to estimate the accuracy of an approximation it to compare it with previous coarser-grained approximations. If the integrand satisfies particular (algorithm-dependent) properties, it is possible for successive approximations to indicate apparent convergence, when the iteration has not in fact converged. A very simple example: trapezium rule integration of a cosine function, using successively finer subdivisions:
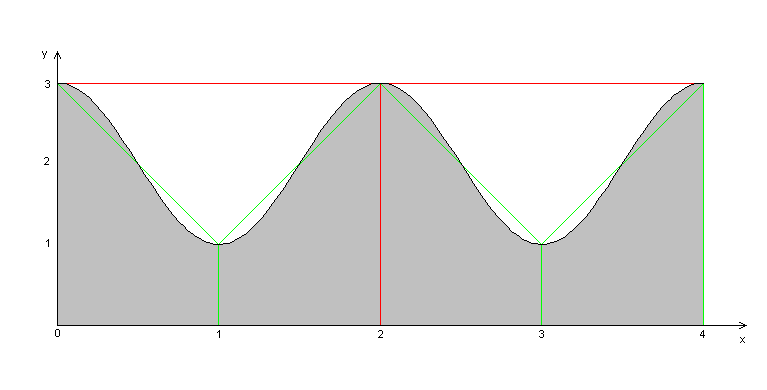
First approximation (integrand values at x= 0,4): 4*(3+3)/2 = 12
Second approximation (integrand values at x=0,2,4): 2*(3+3)/2+2*(3+3)/2 = 12
Third approximation (integrand values at x=0,1,2,3,4): (3+1)/2+(1+3)/2+(3+1)/2+(1+3)/2 = 8
Based on the first two approximations only, we would conclude that the iteration had converged, because the results were the same. We would also have to assume that the result was exact, as we have no variation in the answers, when in fact it is out by 50%. It is only when we consider the third approximation that we can see a difference, and we can judge the error in the approximation.
The pre-R11 ACIS Mass Properties algorithm was susceptible to this problem in some cases, typically when there was some repeated pattern in the geometry, for example, a helical sweep surface. The improved algorithm deals with this by analyzing face/edge tangent directions in order to spot situations where it is missing. An analogous solution for the above example would be to realize that the integrand has the same value at x=0,2 and 4, and guess that the integrand is not in fact constant and that we need to subdivide further.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.