Using Laws for Analysis
Laws can be used to answer questions about entities, such as locating maxima or minima of a curve, what is the closest point between two non-intersecting lines, or where all the roots are.
Finding Singularities
The following example shows how to use laws to find the minimum point on a curve.
Scheme Example
| ; Create the points for a test curve. (define my_plist (list (position 0 0 0)(position 20 20 20) (position -20 20 20)(position 0 0 0))) ;; my_plist ; my_plist => (#[position 0 0 0] #[position 20 20 20] ; #[position -20 20 20] #[position 0 0 0]) (define my_start (gvector 1 1 1)) ;; my_start ; my_start => #[gvector 1 1 1] (define my_end (gvector 1 1 1)) ;; my_end ; my_end => #[gvector 1 1 1] (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; my_testcur => #[entity 2 1] ; Create a curve law. (define my_curlaw (law "map(term(cur(edge1),1),edge1)" my_testcur)) ;; my_curlaw ; my_curlaw => #[law "MAP(TERM(CUR(EDGE1),1),EDGE2)"] ; Find its minimum. (define my_min (law:nmin my_curlaw 0 1)) ;; my_min ; my_min => 0.713060255033984 ; Find the point and mark it. (define my_minpoint (dl-item:point (curve:eval-pos my_testcur my_min))) ;; my_minpoint ; my_minpoint => #[dl-item 22F733F8] (dl-item:display my_minpoint) ;; () |
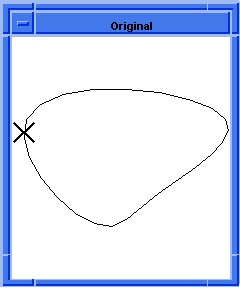
Figure. Minimum Point on a Test Curve
The following example first creates an edge, called my_edge. Then it creates a law, called my_law, that is the composition of three laws. The map law symbol maps that parameter domain of my_edge or edge1 to the closed interval [0,1]. Next my_maxpoint is defined as the numerical minimum of the law my_law over the domain [0.5,1]. Then my_testcur is evaluated at my_maxpoint, and the result is plotted. The plotted point represents the point on the curve that has the lowest x coordinate. By using the laws x, y and z, the law:nmax and law:nmin extensions find a bounding box for my_testcur. The resulting bounding box is within ACIS tolerances.
Scheme Example
| (define my_plist (list (position 0 0 0)(position 20 20 0) (position 40 0 0)(position 60 25 0) (position 40 50 0)(position 20 30 0) (position 0 50 0))) ;; my_plist ; my_plist => (#[position 0 0 0] #[position 20 20 0] ; #[position 40 0 0] #[position 60 25 0] #[position 40 50 0] ; #[position 20 30 0] #[position 0 50 0]) (define my_start (gvector 1 1 0)) ;; my_start ; my_start => #[gvector 1 1 0] (define my_end (gvector -1 1 0)) ;; my_end ; my_end => #[gvector -1 1 0] (define my_testcur (edge:spline my_plist my_start my_end)) ;; my_testcur ; my_testcur => #[entity 2 1] (define my_law (law "map(Curc(edge1),edge1)" my_testcur)) ;; my_law ; my_law => #[law "MAP(CURC(EDGE1),EDGE2)"] (define my_maxpoint (law:nmax my_law 0.5 1)) ;; my_maxpoint ; my_maxpoint => 0.840637305143896 (define my_point (dl-item:point (curve:eval-pos my_testcur my_maxpoint))) ;; my_point ; my_point => #[dl-item 22F793F0] (dl-item:display my_point) ;; () |
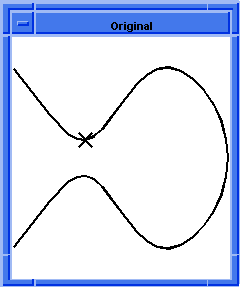
Figure. First Maximum Point on a Test Curve
The example defines my_law to be the law that returns the curvature of my_testcur with its parameter range mapped to [0,1]. The CurC law returns the curvature of its curve. Because the radius of curvature is the reciprocal of the curvature, finding where my_law is maximum finds where the radius of curvature is minimum, or where the tightest turn in the curve is located.
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.