Boolean Operations on Graphs
The graph theory component provides for four types of Boolean operations: unite, intersect, subtract, and lose boundary, and subtract and keep boundary.
Figure. Graph 1 Union with Graph 2 shows the union of graph 1 and graph 2, shown in Figure. Graphs 1 and 2 for Boolean Operations. The result is a graph whose vertices and edges are the union of the vertices and edges of the original graph. As such, there are no duplicate vertices and edges even though they appear in the individual graphs.
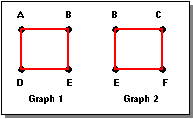
Figure. Graphs 1 and 2 for Boolean Operations
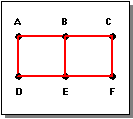
Figure. Graph 1 Union with Graph 2
The following figure shows the intersection of the two graphs which keeps only those vertices and edges that are common to both.
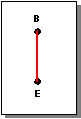
Figure. Graph 1 Intersected with Graph 2
The following two figures show the subtraction operations. The result of subtraction can be ambiguous, because an edge (such as B-E) might be half in a graph. For this reason the subtract method of generic_graph takes a logical option that tells if such edges should be kept or not. Figure. Graph 2 Subtracted from Graph 1 Not Keeping Boundary shows graph 2 subtracted from graph 1 with half edges not kept and Figure. Graph 2 Subtracted from Graph 1 Keeping Boundary show the half edges being kept.
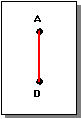
Figure. Graph 2 Subtracted from Graph 1 Not Keeping Boundary
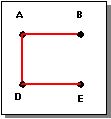
Figure. Graph 2 Subtracted from Graph 1 Keeping Boundary
[Top]
© 1989-2007 Spatial Corp., a Dassault Systèmes company. All rights reserved.